概率统计核心考点测试卷A 参考答案

2019-03-02

中学生数理化(高中版.高考数学) 2019年2期

关键词：乙组甲组晋级

一、选择题

1.C 2.C 3.D 4.B 5.A 6.D

7.A 8.D 9.D 10.B 11.B 12.B

二、填空题

三、解答题

17.(1)记“蚂蚁与三角形的三个顶点的距离均超过1”为事件M。

根据题意,如图1,在△A B C中,A B=3,B C=4,A C=5,A D=A I=B E=B F=C G=CH=1,由图分析可得,△A B C的周长为12,到三角形的三个顶点的距离均超过1的部分为线段D E、F G、H I,即其总长度为6;蚂蚁在三角形的边上爬行,其测度是三角形的周长,故所求概率为

(2)蚂蚁在三角形所在区域内部爬行,其测度是面积,△A B C的面积为离三个顶点的距离都不大于1的地方的面积为,所以其恰在离三个顶点的距离都大于1的地方的概率即为所求概率

18.(1)600÷50=12,第一段的号码为006,第五段抽取的数是6+(5-1)×12=54,即第五段抽取的号码是054。

(2)第四组人数为0.008×10×50=4,设这4人分别为A,B,C,D。

第六组人数为0.004×10×50=2,设这2人分别为x,y,随机抽取2人的可能情况是:

A B A C A D B C B D C D x y A x

A y B x B yC x C yD x D y

共计15种情况,其中他们上班所需时间满足|a-b|＞10的情况有8种,所以满足|a-b|＞10的事件的概率

(3)全体职工中上班所需时间不少于30分钟的职工约有600×(0.008+0.008+0.004)×10=120(人),所以估计企业应有3辆专车。

19.(1)甲乙两人用车时间超过2小时的

所以ξ的分布列为表1:

表1

20.(1)由所给的茎叶图知,甲班50名同学的成绩由小到大排序,排在第25,26位的是108,109,故甲班数学成绩的中位数是108.5,众数是103;乙班48名同学的成绩由小到大排序,排在第24,25位的是106,107,故乙班数学成绩的中位数是106.5,众数为92和101。

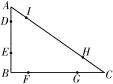
图1

(2)由茎叶图中的数据可知,甲班中数学成绩为优秀的人数为20,优秀率为乙班中数学成绩为优秀的人数为18,优秀率

(3)用甲班学生数学成绩的频率估计概率,则高三学生数学成绩的优秀率又X的所有可能取值为0,1,2,3,X服从二项分布,即

所以X的分布列为表2:

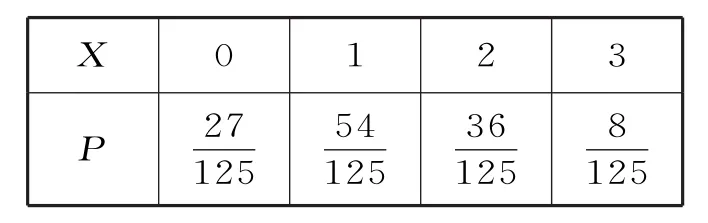
表2

21.(1)因为1000×5%=50,由图可知,甲组有4+10+8+4+2+1+1=30(人),所以乙组有20人。又因为40×60%=24,所以识记停止8小时后,40个音节的保持率大于或等于60%的甲组有1人,乙组有(0.0625+0.0375)×4×20=8(人),所以(1+8)÷5%=180(人),即估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于等于60%的人数为180人。

(2)由图可知,乙组在[12,24)范围内的学生有(0.025+0.025+0.075)×4×20=10(人),在[20,24)范围内的有0.075×4×20=6(人),X的可能取值为0,1,2,3,P(X=0)=

所以X的分布列为表3:

表3

(3)因为2×4+6×10+10×8+14×4+18×2+22×1+26×1=288,所以甲组学生的平均保持率为

因为(6×0.0125+10×0.0125+14×0.025+18×0.025+22×0.075+26×0.0625+30×0.0375)×4×20=432,故乙组学生的平均保持率为

所以临睡前背英语单词记忆效果更好。

22.(1)由频率分布直方图中各小长方形的面积总和为1,可知(2a+0.020+0.030+0.040)×10=1,故a=0.005。

(2)由频率分布直方图知,各小组依次是[50,60),[60,70),[70,80),[80,90),[90100],其中点数据分别为55,65,75,85,95对应的频率分别为0.05,0.30,0.40,0.200.05,故可估计=55×0.05+65×0.3+75×0.4+85×0.2+95×0.05=74(分)。

(3)由频率分布直方图知,晋级成功的频率为0.20+0.05=0.25,故晋级成功的人数为100×0.25=25(人),故填表如表4: