圆锥曲线核心考点测试卷B
2019-03-02河南省项城市第一高级中学
■河南省项城市第一高级中学 郭 丽
一、选择题
1.苹果手机上的商标图案(如图1所示)是以曲线段A B为分界线,裁去一部分图形制作而成的,如果该分界线是一段半径为R的圆弧,且A,B两点间的距离为 2R,那么分界线的长度应为( )。
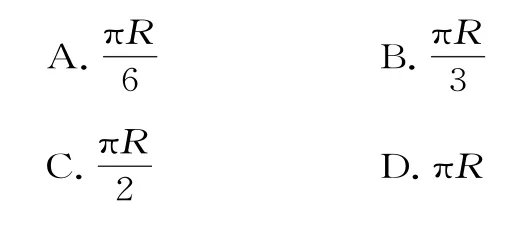

图1
2.已知直线a x+b y+c-2=0(b>0,c>0)经过双曲线的上顶点,则的最小值是( )。

3.如图2,在长方体A B C D-A1B1C1D1中,A B=A D=2A A1=4,O是底面A B C D的中心,E是A1D1的中点,P是底面A B C D上的动点,且到直线O E的距离等于1,对于点P的轨迹,下列说法正确的是( )。

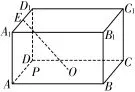
图2
6.已知点A(-2,0),B(2,0),P(x0,y0是直线y=x+4上任意一点,以A,B为焦点的椭圆过点P,记椭圆的离心率e关于x0的函数为e(x0),那么下列结论中正确的是( )。
A.e与x0一一对应
B.函数e(x0)是增函数
C.函数e(x0)无最小值,有最大值
D.函数e(x0)有最小值,无最大值
7.过抛物线y2=2p x(p>0)的焦点F作斜率大于0的直线l交抛物线于A,B两点(A在B的上方),且l与准线交于点C,若


9.如图3,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦A P,A Q。设直线P Q过点T(5,-2),则以P Q为底边的等腰三角形A P Q的个数为( )。
A.1 B.2
C.3 D.4
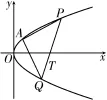
图3
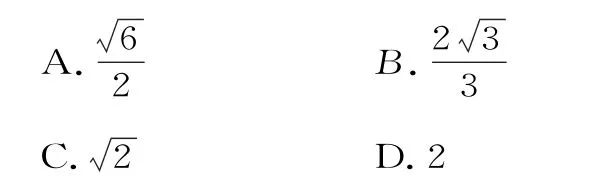
11.已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,若△P F1F2是以P F1为底边的等腰三角形,椭圆与双曲线的离心率分别为e1,e2,则e1·e2的取值范围是( )。
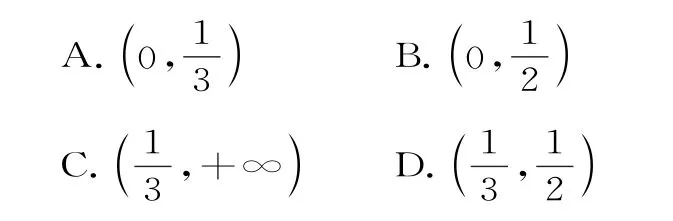
12.如图4,已知抛物线C的方程为y2=2p x(p>0),一条长度为4p的线段A B的两个端点在抛物线C上运动,则线段A B的中点D到y轴距离的最小值为( )。
二、填空题
13.如图5,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为____。
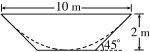
图5
15.已知A,B为抛物线y2=2x上两个动点,O为坐标原点,且O A⊥O B,若直线A B的倾斜角为135°,则S△AOB=____。
三、解答题
17.某市为改善市民出行,准备规划道路建设。规划中的道路M-N-P如图6所示,已知A,B是东西方向主干道边上的两个景点,且它们到城市中心O的距离均为是正北方向主干道边上的一个景点,且到城市中心O的距离为4k m,线路MN段上的任意一点到景点A的距离比到景点B的距离都多1 6k m,其中道路起点M到东西方向主干道的距离为6k m,线路NP段上的任意一点到O的距离都相等。以O为原点,线段A B所在直线为x轴建立平面直角坐标系x O y。
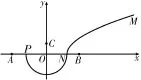
图6
(1)求道路M-N-P的曲线方程;
(2)现要在道路M-N-P上建一站点Q,使得Q到景点C的距离最近,问:如何设置站点Q的位置(即确定点Q的坐标)?
18.在直角坐标系x O y中,抛物线C的
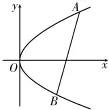
图4
(1)求抛物线C的方程。
(2)若点P(t,1)(t>0)为抛物线C上的定点,A,B为抛物线C上两个动点,且P A⊥P B,问:直线A B是否经过定点?若是,求出该定点;若不是,说明理由。
19.已知F,F′分别是椭圆C1:1 7x2+1 6y2=下>的上下焦点,直线l1过点F′且垂直于椭圆长轴,动直线l2垂直l1于点G,线段G F的垂直平分线交l2于点H,点H的轨迹为C2。
(1)求轨迹C2的方程。
(2)若动点P在直线l:x-y-2=0上运动,且过点P作轨迹C2的两条切线P A,P B,切点为A,B,试猜想∠P F A与∠P F B的大小关系,并证明你的结论的正确性。
(1)求椭圆C的方程。
(2)设P是椭圆C上的一个动点,且点P在y轴的右侧,直线P A,P B与直线x=4分别交于M,N两点。若以MN为直径的圆与x轴交于E,F两点,求点P横坐标的取值范围及|E F|的最大值。
21.已知双曲线C的中心在原点,D(1,0)是它的一个顶点,d=(1,2)是它的一条渐近线的一个方向向量。
(1)求双曲线C的方程。
(2)若过点(-3,0)任意作一条直线与双曲线C交于A,B两点(A,B都不同于点D),求证为定值。
情形二:抛物线y2=2p x(p>0)及它的顶点;
22.如图7,在平面直角坐标系x O y中,已知R(x0,y0)是椭圆的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于点P,Q。
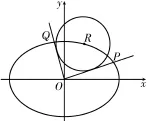
图7
(1)若点R在第一象限,且直线O P,O Q互相垂直,求圆R的方程。
(2)若直线O P,O Q的斜率存在,并记为k1,k2,求k1·k2的值。
(3)试问:O P2+O Q2是否为定值?若是,求出该值;若不是,说明理由。
