圆锥曲线核心考点测试卷B 参考答案

一、选择题

1.C 2.A 3.A 4.D 5.A 6.C

7.A 8.D 9.A 10.B 11.C 12.C

二、填空题

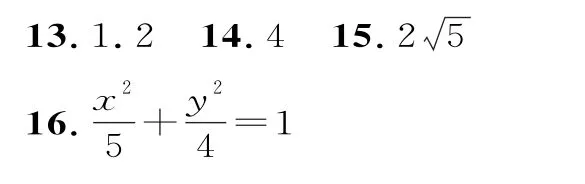
三、解答题

17.(1)根据题意,线路MN段上的任意一点到景点A的距离比到景点B的距离都多16

km,则线路MN所在的曲线是以定点A、B为左右焦点的双曲线的右上支,其方程为x2-y2=64(8≤x≤10,0≤y≤6)。又线路NP段上的任意一点到O的距离都相等,则线路NP所在的曲线是以O为圆心,ON为半径的圆,其方程为x2+y2=64(-8≤x≤8,y≤0)。

故道路M-N-P的曲线方程为MN段x2-y2=64(8≤x≤10,0≤y≤6);NP段x2+y2=64(-8≤x≤8,y≤0)。

(2)当Q在线路MN上,设Q(x0,y0)。

分析可得,当y0=2时,|C Q|有最小值且

当Q在线路NP上时,设Q(x0,y0)。

分析可得,当y0=0时,|C Q|有最小值,且

18.(1)双曲线1,焦点为(0,±1),抛物线C的顶点是O,可得抛物线C的方程为x2=4y或x2=-4y。

(2)若点P(t,1)(t＞0)为抛物线C上的定点,则抛物线的方程为x2=4y,即有P(2,1),设

19.(1)因为1 7x2+1 6y2=2/,所以x2=1,所以椭圆的半焦距长为

所以轨迹C2的方程是x2=y。

(2)猜想∠P F A=∠P F B。

所以cos∠A F P=cos∠B F P。

所以∠P F A=∠P F B。

(2)方法一:设P(x0,y0)(0＜x0≤2),因为A(0,-1),B(0,1),所以直线P A的方程为

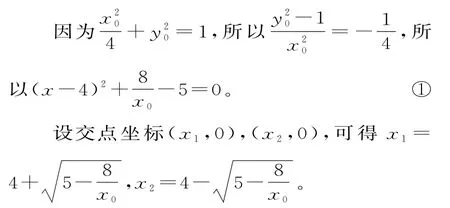
所以当x0=2时,该圆被x轴截得的弦长的最大值为2。

方法二:设P(x0,y0)(0＜x0≤2),A(0,-1),B(0,1),所以,直线P A的方程为

(2)当直线A B垂直于x轴时,其方程为x=-3,A,B的坐标为(-3,4),(-3,-4)

当直线A B不与x轴垂直时,设此直线方程为y=k(x+3)。

设A(x1,y1),B(x2,y2),则x1+x2=

(3)当M,N满足EM⊥EN时,取M,N关于x轴对称的点为M′,N′,由对称性知EM′⊥EN′,此时MN与M′N′所在直线关于x轴对称,若直线MN过定点,则定点必在x轴上。

设直线MN的方程为x=m y+t。

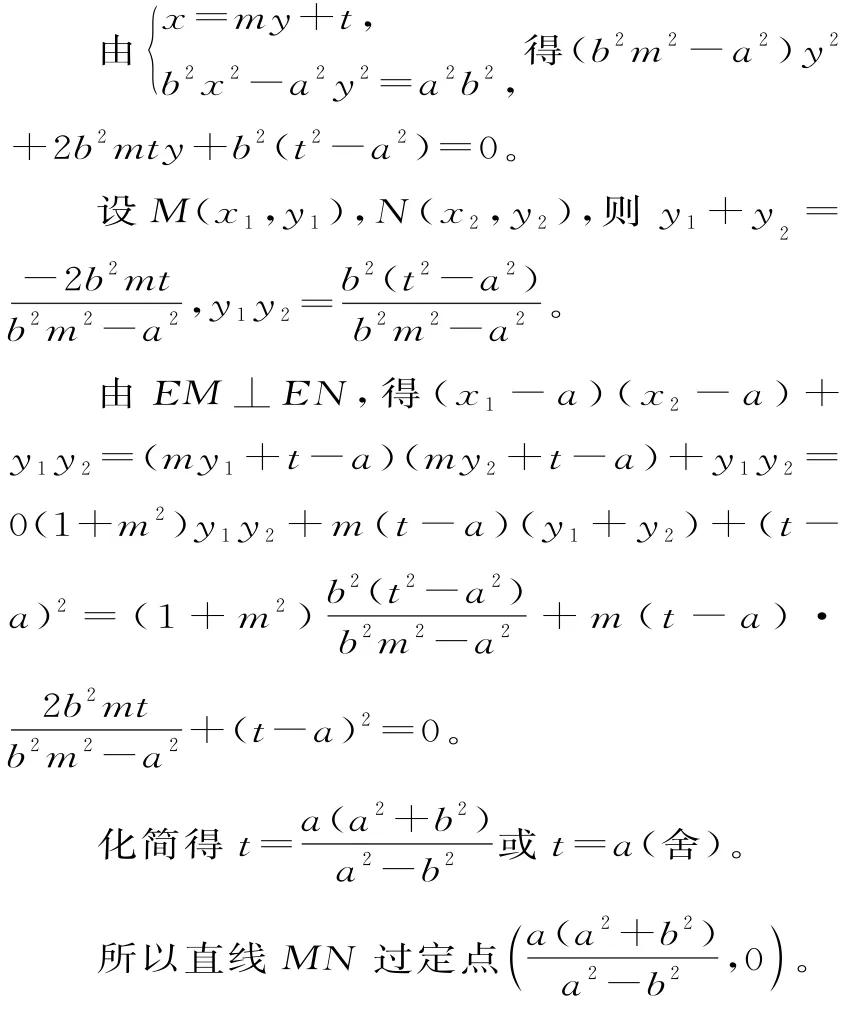
情形二:在抛物线y2=2p x(p＞0)中,若M,N为抛物线上的两点(都不同于原点O),且OM⊥ON,则直线MN过定点(2p,0)。

(2)在椭圆中,若E′为它的左顶点,M,N为椭圆上的两点(都不同于点E′),且E′M⊥E′N,则直线MN过定点(3)在椭圆中,若F为它的上顶点,M,N为椭圆上的两点(都不同于点F),且FM⊥FN,则直线MN过定点

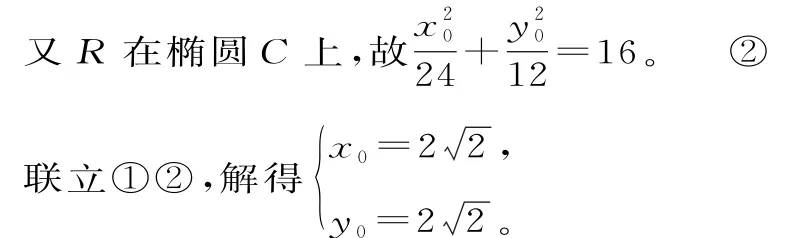
(2)因为直线O P:y=k1x和O Q:y=k2x都与圆R相切,所以两边平方可得k,k为12方程的两根,可得

因为点R(x0,y0)在椭圆C上,所以

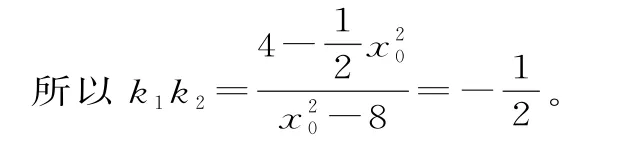
(3)①方法一:当直线O P,O Q不落在坐标轴上时,设P(x1,y1),Q(x2,y2)。

由(2)知2k1k2+1=0,所以

因为P(x1,y1),Q(x2,y2)在椭圆C上,所以

方法二:当直线O P,O Q不落在坐标轴上时,设P(x1,y1),Q(x2,y2)。

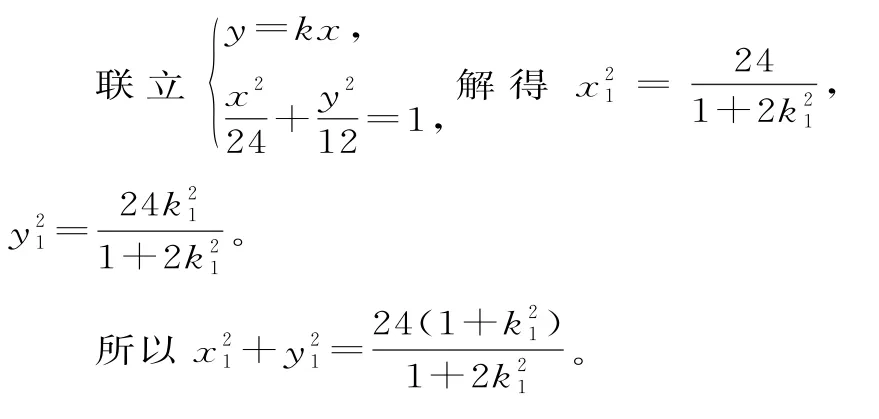
②当直线O P,O Q落在坐标轴上时,显然有O P2+O Q2=36。

综上,O P2+O Q2=36。