二维偏振无关全吸收光栅传感器的研究

2019-03-01徐天宇宋建林赵建行周见红

长春理工大学学报（自然科学版） 2019年1期

徐天宇，宋建林，赵建行，周见红

（长春理工大学光电工程学院，长春 130022）

自1902年wood等人观测到等离子体波的存在后，金属纳米结构的表面等离激元吸收增强特性就被应用到了各个方面，例如太阳能，光探测器，热辐射器件等[1-6]。由于金属结构对结构形状和周围环境因素十分敏感，使其在折射率传感器方面的应用也受到了广泛的关注。2010年Jan Becker等人定义了一个无量纲的品质因数FOM*（FOM*=max|[dI(λ)/dn(λ)]/(I(λ)|）来评定结构的传感精度[7]。基于此，Na Liu等人提出了一种柱状结构，其在1.6μm可以达到全吸收，该结构针对葡萄糖的FOM*值可以达到87。2015年周文超等人设计了一种铝材料的二维光栅，其在折射率0.02步长变化时，峰值波长变化0.005μm[10]。事实上，提高金属纳米结构传感器的有效精度仍然是一个挑战。

在研究中，设计了一种基于表面等离激元增强吸收的新型二维全吸收光栅结构。吸收峰值波长随结构尺寸参数线性变化，吸收效率始终接近100%，此结构由于其对称性不仅偏振无关，而且在TM偏振和TE偏振下对20°以内的入射角度也并不敏感。在折射率分辨上更是具有十分良好的性能，它的FOM*值可达到300，可以作为折射率传感器。

1 结构设计与模拟方法

图1给出了二维偏振无关光栅结构的计算模型。该结构由周期排列的六棱柱及基底构成。在仿真模型中，六棱柱被看做由四棱柱削掉四个全等三棱柱得到，如图1（b）和（c）所示，六棱柱的高度为h，四棱柱边长为a，截去三角形后所剩边长为b，棱柱间隙为w=2w1，结构周期为p。结构所选用的材料为金，在数值模拟中，材料的光学常数采用由实验确定的介电函数[11]。

为了分析此结构的光学传感特性，研究中采用二维有限差分时域（FDTD）方法在近红外波段进行仿真模拟。在数值模拟中，沿x轴及y轴采用周期边界（periodic）条件，沿z轴的边界应用完美匹配层（PML）条件。平面波从空气一侧照射结构，两个面监视器分别放置在空气中及基底内以获得反射率和透过率，另外两个面监视器分别放置在x-y面及x-z面监测结构不同位置处的电场。

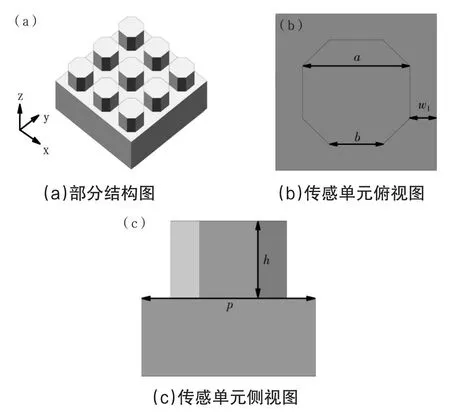
图1 二维周期光栅传感器模型

2 仿真结果及讨论

2.1 阻抗分析

图2（a）为吸收结构的反射谱和吸收谱，其中，结构参数分别为p=500nm，w=50nm，h=1000nm，a=450nm，b=200nm。由于结构的透过率无限接近0，所以吸收公式为A=1-R，式中A与R分别是吸收率和反射率。可以看到共振吸收峰位于波长为818nm的位置。对于这个结果，可以利用阻抗原理进行解释，反射率和吸收率的阻抗为[12]：

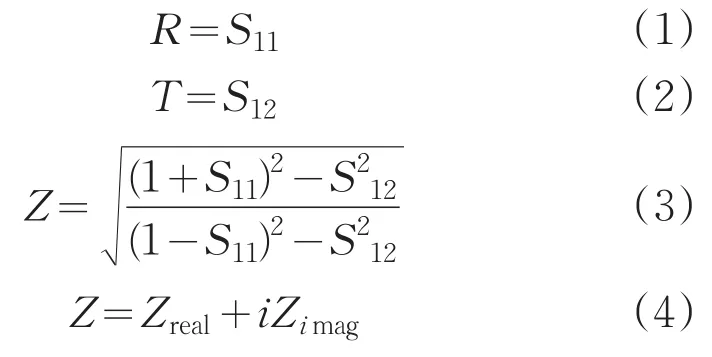
结构反射率与其阻抗的实部和虚部曲线如图2（b）。方块曲线为反射率，圆圈曲线与三角曲线分别代表阻抗的实部与虚部。则有：

在818nm处得到Z=1.13+0.18i，利用公式（5），可得出R≈0。与图2（a）中结果一致。

图2 传感结构的吸收特性及阻抗曲线

2.2 电场分布

为了进一步研究该结构的物理机制，图3给出了在818nm峰值波长处的电场（EZ）。由图可知，在平面波沿x方向偏振时，光能量主要集中在沿y方向的结构表面以及狭缝中，这是由于等离激元在结构表面共振形成了局域增强，并且沿着狭缝在传输过程中形成等离激元增强，使得结构可以在818nm处将入射光能量完全吸收。

图3 光栅传感结构在818nm处的电场分布

2.3 参数影响

由于图3给出了通过对图2的结构控制变量得出的吸收峰值波长与各参数之间的关系，所以针对结构的各个参数对吸收峰值波长的影响进行分析。尽管研究的纳米结构并非规则二维矩形光栅，但是其峰值移动仍满足如下关系：，λpeak∝b[10]。共振峰值波长与光栅结构的厚度相关，随着高度的增加，峰值线性红移。而间隙宽度以及b值对于结构吸收峰值的影响可以通过由填充因子（SA和SB分别是结构单元六棱柱和基底的横截面积）决定的有效折射率来进行分析。结构间隙w减小或者b值增大都会使填充因子增大，结构的有效折射率增加，峰值红移。

图4 吸收峰值波长与结构中六棱柱参数之间的关系曲线

2.4 入射角度影响

图5 结构在不同入射角度下的反射谱

图5给出了结构在TM偏振以及TE偏振下入射角度变化时的反射谱。可以看出，吸收峰值波长对20°以内的入射角度并不敏感，并且能够保证在峰值波长处全吸收。在TM和TE两种偏振下，结构对不同的入射角度的响应是不同的。在TM偏振下入射角度对吸收峰值波长的影响要比TE偏振大，这是由于TM偏振作为横磁模，可以强烈的激发磁场共振或者表面等离激元，而作为横电模的TE偏振却不具有这一特性。结构对20°内的入射角度不敏感使其在折射率传感器的应用上增加了实用性，即使探测时光与器件有小角度偏差，计算结果仍然能够能够保证相对准确。

2.5 传感特性分析

本文的结构除上述这些特性以外，其共振波长也可以由所处介质的折射率确定。为此对这个结构对于不同折射率下的传感特性做了研究。图6（a）展示了在不同葡萄糖浓度时结构所对应的不同折射率下的反射谱。通常情况下，RI传感器的灵敏度可以定义为波长变化与折射率变化的比率。当RI范围从1.312到1.352，步长为0.01时，可以得到不同的波长，分别为1.056μm，1.064μm，1.071μm，1.079μm ，1.086μm。也就是步长为0.02时，峰值波长变化0.016μm，对比周文超等人的研究结果，有了显著提高[10]。

依据Jan Becker等人[7]对FOM*值的定义，通过公式（6）

计算FOM*的值，公式中，ΔI(λ)/I(λ)是强度相对变化，Δn是折射率改变量，λ0为两个折射率强度之差的最大值对应的峰值波长。图6（b）给出了葡萄糖相对于水（n=1.312）的结构的FOM*值的变化，可以看出，FOM*值最大可达到310，与文中提及的传感器结构相比得到了优化。FOM*的峰值波长并未与吸收峰值波长完全对应，这种失谐在J.Becker等人的等离子体传感器实验中得到了论证。