基于光纤声呐传感器混沌锁频方法研究

刘丹，衣文索，杜洋，张叶浩

（长春理工大学 光电工程学院，长春 130022）

随着海洋资源的不断开发与海岛防御工程的技术革新，水下目标的隐蔽性逐渐增强，探测难度加大，因此水下声信号特征识别成为水下通信与探测的热点研究问题之一[1-3]。传统压电陶瓷类声呐传感器体积大、成本高、探测范围小，难以接收水下微弱的目标声信号。光纤声呐作为先进水声探测传感器，具有灵敏度高、抗电磁干扰能力强、动态范围大、损耗小，易于传输等优势，是光纤光学与光电子学及水声学相互融合的新兴技术[4-5]。目前广泛应用的为干涉型光纤声呐传感器，通过对调制相位的解调后进行频率分析提取水下声信号的信息，频率作为识别水声信号的重要特征，一直是众多学者关注的焦点。段海鹏等设计了一种基于迈克尔逊干涉仪的激光光路，可实现对中低频声信号的频率识别[6]。张晓琳等提出了基于Morlet小波对水面散射光与参考光的干涉信号解调方法，可探测1 KHz-15 KHz水下声信号[7]。曹增辉等利用激光相干技术对采集的水面干涉信号进行解调，该方法可实现对水下目标信号的频率和强度特征提取[8]。张烈山等提出基于改进相位生成载波解调的激光相干探测方法，频率探测下限可达 30Hz[9]。

上述方法探测范围多趋向于中频段，不能有效降低环境噪声对微弱目标信号识别的干扰。针对以上问题，文中首先利用干涉型光纤声呐进行高灵敏度的水下低频微弱声信号探测，然后通过光电转换将干涉光信号转换为电信号并送入Duffing振子检测模块，模拟强混响环境下进行低频段扫描锁频，探测范围下限可达10Hz。混沌系统具有较高的检测灵敏度和较好的抗噪声性能，是水下低频微弱声波信号检测不可或缺的技术之一。

1 光纤声呐混沌锁频原理

1.1 声压信号调制原理

干涉型光纤声呐传感器采用Mach-Zehnder干涉仪结构进行声信号探测，结合相位生成载波方法提取声压信号，如图1所示，内调制激光由一端射入，在耦合器C1处等功率分成两束光，两束光分别进入传感臂和参考臂，声压信号作用在传感臂上，并在耦合器C2合束发生干涉效应。则该干涉光含有声压信号的各类特征，干涉后的光信号经由传输光纤到达光电探测器，在光电探测器处实现光信号到电信号的转换，将转换后的信号输入上位机对声压信号的提取。

图1 声压信号调制原理图

通常水下声信号为：

其中，P为声压，a为声压幅值，ωs为声压信号的角频率，t为时间[10-11]。当水下声压以机械振动形式到达光纤声呐传感器，声信号的强弱转换为干涉信号的强弱，干涉后的光强信号经过光电转换器和跨阻放大器将光电流信号转换成电压信号，实现声-光-电的转换。电压信号V表示为：

其中，V1，V2均为与光强信号和光电转换器的响应度成线性比例的常量，acos(ωst)是由声压信号引起的调制相位偏移量，C为由载波信号引入的调制幅度，ωm为载波信号角频率，φ0表示两臂干涉的初始相位[12-13]。φn(t)为由噪声环境引起的随机相位。由（2）式可知调制在余弦函数中声压信号，通过在上位机中将转换后的电信号分别乘以Gcosωmt和Hcos2ωmt后进行低通滤波与微分后交叉相乘再相减，最后积分提取声压信号。可得出声压信号P与输出电压V0的关系表达式如下：

式中，fP为声信号解调后的附加增益，η(t)信号接收及处理过程中的噪声干扰信号[14]。实际工程应用中噪声对微弱水声信号检测造成很大干扰，导致声压频率特征很难识别，需进一步进行声压频率的辨别。

1.2 混沌微弱信号检测原理

混沌理论作为弱信号检测新技术，摒弃了传统的滤波技术或抑制噪声的方法，利用混沌系统对初始条件的敏感性及对噪声的“免疫性”，从强噪声中提取有用信号，具有良好的抗噪声性能。Duffing方程是目前周期信号检测常用的模型之一，其表达式为：

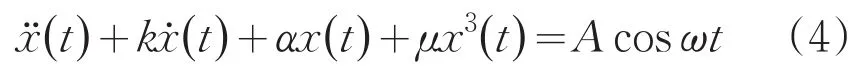
式中，α是线性恢复力系数，k是阻尼比，μ是非线性恢复力系数，Acosωt是周期外力策动力，A，ω分别为周期策动力幅值和策动力角频率[15]。当α=-1，μ=1时，方程为：

将上式进行线性变换得：

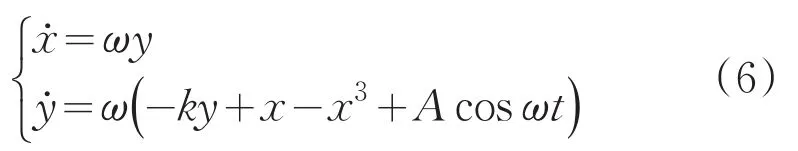
当将系统的周期策动力幅值由零逐渐增加时，系统的相位图将发生规律性变化，遍历了振荡、同宿、分岔、混沌、混沌临界以及大尺度周期轨迹[16]。图2中（a）、（b）为分别当A=0.8264为混沌临界状态，当A=0.8265为大尺度周期态。在Duffing系统处于混沌临界状态下，即使增加很小的幅值，系统(x,y)相位运动轨迹也会向大尺度周期态转变。混沌临界状态可根据Melnikov函数计算系统的相变阈值，其阈值γ表达式：

当k=0.5，ω=10时，A取不同值时其非线性动力学相位图如图2[17-18]。

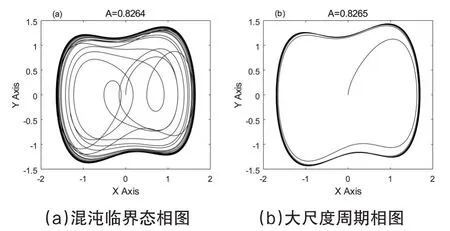
图2 Duffing振子相位轨迹图

2 Duffing混沌系统微弱信号频率检测

Duffing混沌系统为动力学复杂的非线性系统，当检测系统加入待测信号后，根据（4）式可变换新的数学检测模型，得到方程如下：

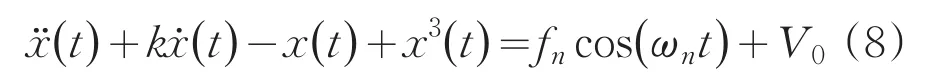
将（3）式代入得：

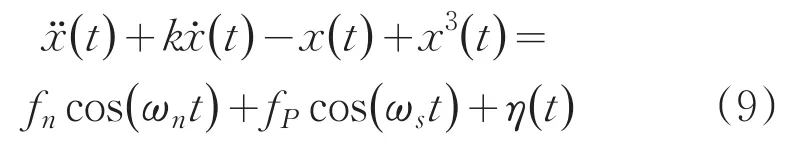
整理后得等价方程为：

式中，k=0.5，fccos(ωnt)为系统的周期策动力信号，fPcos(ωst)为待测信号，η(t)为待测信号中混入的噪声。

图3 Duffing振子锁频原理图

Duffing振子检测原理如图3所示，激励模块为可控信号发生器，即fccos(ωnt) ，由（7）式阈值判据式得不同频率策动力对应阈值不同，根据输入的周期策动力频率调节幅值至混沌临界态，再将待测信号输入混沌锁频模块进行检测，当待测信号中含有与输入信号中同频信号存在时，显示模块（X，Y）相平面Duffing混沌系统动力学轨迹将变换为大尺度周期态，否则仍为混沌临界态。根据（10）式在MATLAB/Simulink环境下建立仿真模型，进行仿真实验，如图4所示。

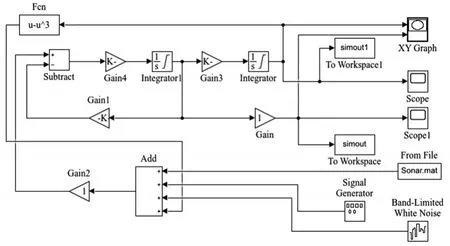
图4 仿真模型图

在此仿真模型中，将待测微弱声信号的数据存放在From File模块中，Signal Generator模块为可调激励信号输入端，其频率与阈值相对改变，Band-Limited White Noise模块用于产生白噪声，时域的输出波形可在示波器Scope中查看，系统相图可通过XY Graph显示。

3 仿真结果

在图4所示的仿真模型中输入模拟的声压信号及存在的噪声，信噪比为-65dB，设置仿真系统频率检测范围为0.8KHz～1.2KHz，检测模型中激励信号的频率以10Hz/s的速度增加，其不同频率时的混沌系统阈值根据计算机计算后也每秒对应变换，且图4中的Gain3和Gain4模块中增益参数与频率速度相同，以10/s增加，以确保激励信号不同时其Duffing系统一直处于混沌临界状态，则系统初始状态如图5所示，图5（a）为XY Graph显示模块中混沌临界状态、图5（b）为Scope模块混沌临界态的时域波形图。设模拟声呐信号是频率为1KHz幅值为0.1的微弱中频信号，图6中分别为（a）待测信号波形图、（b）为信噪比为-65dB的时域波形图，可以看出待测的微弱信号完全淹没在噪声中。将待测微弱信号与噪声信号输入到锁频模块中，当激励模块输入频率增加至1KHz时，显示模块的相位图及时域波形图将发生改变，如图7所示，其XY Graph模块运动轨迹由混沌临界状态转变为大尺度周期态，且时域波形图将成规律性变化，此时停止仿真完成此次微弱信号的频率锁定。

当声压信号为低频微弱信号时，重新设置频率检测范围为10Hz～100Hz，此时可调整扫频步长为1Hz/s，其模型参数调整同上Gain3与Gain4增益参数1/s增长，系统初始状态如图8。若待测信号是幅值为0.1，频率为20Hz的低频微弱信号，信噪比不变，如图9（a）、（b）分别为低频微弱信号的波形图，同理待测信号完全隐藏下噪声中。将待测的低频微弱信号和噪声加入重现调整锁频系统后，当激励信号增加至20Hz时，Duffing混沌系统的相位轨迹及时域波形图发生变化，如图10所示。

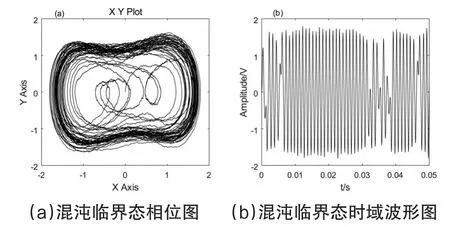
图5 系统初始状态相位图与时域图

图6 微弱中频信号波形图

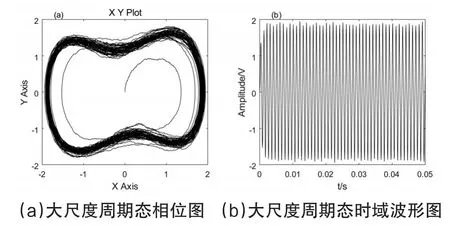
图7 频率锁定相位图及时域波形图

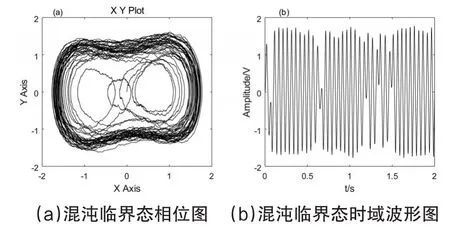
图8 系统初始状态相位图与时域图

图9 微弱低频信号波形图

图10 频率锁定相位图及时域波形图

通过仿真实验可以看出，基于光纤声呐传感器的Duffing混沌锁频系统，无需进行滤波去噪过程，其抗噪性极强，可以直接从噪声中识别微弱的目标信号。并且此系统不但对中频微弱信号敏锐，对低频的微弱信号同样适用。锁频范围可根据待测频率进行调整，频率检测范围宽，精度高，响应时间快，对待测信号的频率特征辨别能力强。

4 结语

基于光纤声呐传感器的混沌锁频方法，将Duffing振子应用于水下弱信号识别之中，把干涉型光纤声呐与Duffing混沌检测的优势有效结合起来，进行水下目标信号低频微弱信号的识别，可以实现在信噪比为-65dB强噪声环境下对频率为20Hz微弱周期信号的辨别。此检测方法灵敏度高，弱信号提取能力强，不受强混响环境限制。