基于不同梁理论的功能梯度悬臂梁自由振动分析

伏培林， 牛国浩， 胡冰晖， 秦明浩， 阚前华

(西南交通大学力学与工程学院， 成都 610031)

引 言

功能梯度材料(Functionally Graded Material，FGM)[1-4]是一种新兴的复合材料，其力学性能随组分材料体积分数的连续变化表现出沿特定方向的梯度分布，可以有效避免由于组分材料界面突变而导致的应力集中现象，从而广泛应用于航空航天等高技术领域[5-10]。由FGM构成的梁便是所谓的功能梯度梁(Functionally Graded Beam, FGB)。

梁的横向振动是一种常见的工程现象。例如：航空发动机的I级压气机叶片的振动实际上可简化为等截面旋转薄壁功能梯度悬臂梁的振动[10]；微悬臂梁的谐振特性可用于高灵敏度的生物传感器, 例如原子力显微镜、表面探测器、生化传感器以及气敏传感器等[11]。当外部激励的频率与梁横向振动的固有频率相等时，梁便会发生共振，其挠度和应力值很容易达到危险水平，进而导致梁构件的破坏[12]。因此，针对梁横向振动问题的研究,长期以来受到了科学家和工程界的广泛关注。伯努利和欧拉在梁振动的理论分析方面做出了开创性的成果，提出了著名的平截面假设，认为梁横截面在振动变形前后始终为垂直于轴线的平面。基于该假设的梁理论便是所谓的欧拉-伯努利梁理论[13]。Sankar[14]基于欧拉-伯努利梁理论进行了功能梯度简支梁的静态分析。瑞利在欧拉-伯努利梁模型的基础上，进一步考虑了梁弯曲对转动惯量的影响，提出了瑞利梁理论。Jockovic等[15]利用等几何方法进行了欧拉-伯努利和瑞利梁的线性自由振动分析，提出了一种基于微分几何与柯西连续梁模型基本关系的新方法，并将其成功应用于空间曲梁单元的刚度及一致质量矩阵的推导；唐安烨等[16]采用积分方程法给出了悬臂瑞利梁固有频率的数值解；Tang等[17]基于Hamilton原理，采用积分方程法进行了旋转锥形悬臂瑞利梁的自由振动分析。铁木辛柯梁理论则是在瑞利梁理论的基础上进一步考虑了剪切变形对振动变形的影响，可用于非细长梁的振动分析[18]。金晶和刑誉峰[19]基于傅里叶变换和边界元法，讨论了具有两个广义位移的剪切梁的自由振动问题。Li等[20]提出了一种功能梯度梁自由振动分析的普适方法，推导出了功能梯度铁木辛柯梁自由振动方程的一般解，讨论了材料性能梯度分布指数对固有频率和模态形状的影响。

本文基于铁木辛柯梁理论，采用分离变量法，给出了FGB固有频率的解析解，比较了在不同跨深比和材料性能梯度分布下欧拉-伯努利、瑞利和铁木辛柯梁理论所给出的前三阶固有频率计算结果，讨论了不同梁理论的适用范围，进而为FGB的设计和应用提供一定参考。

1 FGB振动微分方程及其固有频率

考虑如图1所示的FGB，其中q为横向激振分布载荷，梁的横向弯曲挠度为W(x,t)，L为梁的跨度，b和h分别表示横截面的宽度和高度。材料的密度和模量均沿梁高方向呈梯度分布，记密度为ρ(y)，弹性模量为E(y)，剪切模量为G(y)。

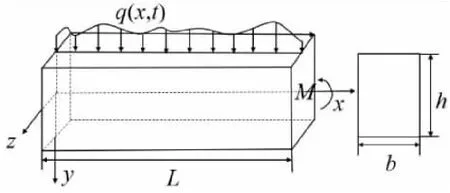
图1 功能梯度悬臂梁模型图

相应的平衡方程为[21]：

(1)

式中，w和θ分别表示梁的弯曲挠度和转角；Q和M分别表示剪力和弯矩；m和Ψ分别为纵向单位长度上的质量和转动惯量，

(2)

(3)

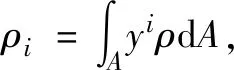
Ψ=ρ2+δ2ρ0-2δρ1

(4)

同时，由质心的定义很容易推导出

(5)

将式(5)代入式(4)中，可得

(6)

为了将内力(Q和M)与梁的振动变形(w和θ)联系起来，还需要引入材料的物理方程

(7)

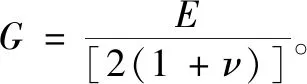
(8)

纵向位移u的表达式满足梁的平截面假设，即

u=u0-yθ

(9)

u0为横截面形心处的纵向位移。将式(8)和式(9)代入式(7)中，即可得到

(10)

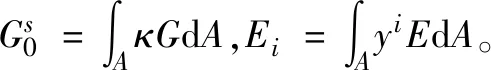
(11)

将式(8)和式(9)代入式(11)中，可得

(12)

从而剪力Q和弯矩M可重新写成如下形式

(13)

将式(2)、式(6)和式(13)代入平衡方程(1)中，便可获得与文献[20]相同的功能梯度铁木辛柯梁振动方程

(14)

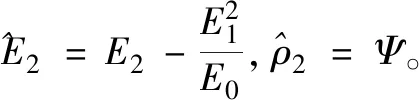
为了便于后续的分析，有必要将同时存在w和θ这两个未知量的方程转化成仅含有单个未知量的方程。因此，引入辅助函数F[20,22]，且

(15)

方程可以转化为

(16)

当梁发生自由振动时，载荷q等于0，自由振动方程(1)可写为：

(17)

令F(x,t)=f(x)exp(iωt)，ω为梁振动固有频率。代入其自由振动方程式，可得：

(18)

显然，二阶常系数齐次微分方程的通解可以写为：

f(x)=Acos(αx)+Bsin(αx)+

Ccosh(βx)+Dsinh(βx)

(19)

其中，A、B、C和D是由梁的左右两端边界条件所决定的积分常数，且

(20)

(21)

悬臂梁的边界条件为：F(x=0)=θ(x=0)=0；Q(x=L)=M(x=L)=0

将边界条件代入F(x,t)得：

F(x=0)=A+C=0

(22)

F′(x=0)=αB+βD=0

(23)

Q(x=L)=(μ1-1)αAsin(αL)-

(μ1-1)αBcos(αL)-(μ2-1)βCcosh(βL)-

(μ2-1)βDsinh(βL)=0

(24)

M(x=L)=-α2Acos(αL)-α2Bsin(αL)+

β2Ccosh(βL)+β2Dsinh(βL)=0

(25)

其中：

进一步整理成线性方程组形式如下：

D(A,B,C,D)T=0

(26)

其中，

显然，积分常数不可能全为零，线性方程组(26)存在非零解，因此系数矩阵D的行列式为零，即

det(D)=0

(27)

求解式(27)即可获得功能梯度悬臂梁的固有频率。

2 结果和讨论

根据式(17)不难发现：跨深比的数值会直接影响梁的固有频率。因此，本节将基于上述的铁木辛柯梁理论，讨论不同跨深比和材料性能分布梯度指数对固有频率的影响。

使用有限元分析软件ABAQUS建立实体梁模型：横截面高h=0.2 m，宽b=0.2 m，通过改变长度L来改变跨深比。由于ABAQUS无法直接设置材料性能的连续梯度分布，因此在有限元模拟中可采用层合梁模型来近似代替真实的FGB。根据材料性能梯度分布函数，计算出每一层梁中间位置的弹性模量、剪切模量和密度，并将其赋予该梁层。在层合梁层数的优化过程中发现，层数为32时的有限元计算结果与理论计算结果符合得较好，因此将在后续的有限元模拟中均将真实的FGB用32层层合梁近似代替。对该模型一端施加完全固定约束，模型整体限制沿z轴移动与绕x、y轴转动的自由度；采用C3D8R单元，单元数目共25 000个。

FGB的材料性能分布可表达如下[16]：

(28)

(29)

其中，ρl和El分别为y=-0.1 m处材料密度和弹性模量，ρu和Eu分别为y=0.1 m处材料的密度和弹性模量，如表1所示；k为材料性能梯度分布指数，如此可反映材料性质的梯度分布情况，如图2所示。

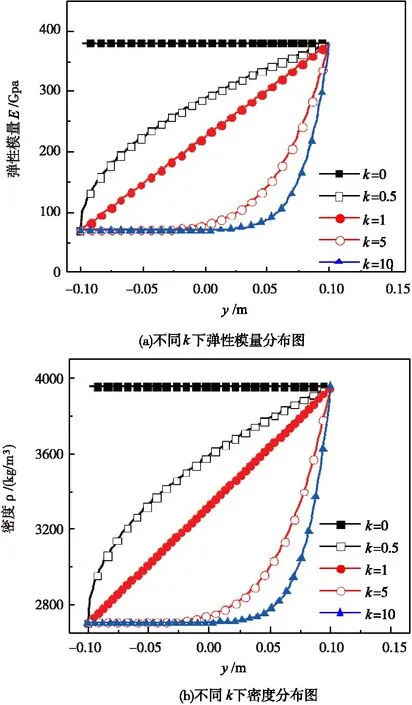
图2 不同性能梯度分布指数k下的弹性模量与密度分布曲线

表1 功能梯度材料属性

从特征方程根的表达式(15)和(16)可以看出，梁的宽度不会影响固有频率，因此梁的几何形状对固有频率的影响仅由跨深比来反映。为了便于后续的讨论，可对固有频率进行如下的无量纲处理：

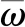
2.1 梯度分布指数对固有频率的影响

分别采用欧拉、瑞利和铁木辛柯梁理论，计算跨深比L/h=10的功能梯度悬臂梁的前三阶固有频率，计算结果如图3所示。从中可以看出，固有频率随着梯度分布指数k的增加而降低，k大于5之后，固有频率趋于稳定，这是由于k大于5时的材料性能分布形式相近(见图2)造成的。在工程上可以采用改变材料性能梯度分布指数的方法调控固有频率来避免目标阶次的共振问题。整体来说，当跨深比为10时，与欧拉-伯努利梁和瑞利梁理论相比，铁木辛柯梁理论所给出的计算结果与有限元结果更为相近，误差均小于5%，处于工程应用接受范围内，表明该理论在此条件下计算低阶固有频率时是可靠的。

图3 梯度分布指数改变时三种梁理论下悬臂梁的固有频率计算结果

2.2 跨深比对固有频率的影响

当梯度分布指数为0.5时，采用三种梁理论，计算不同跨深比时功能梯度悬臂梁的固有频率的结果如图4所示。由图4可以看出，梁的固有频率随着跨深比的增加而增加，且阶数越高，对应固有频率的增加幅度越大，但与有限元解之间的误差也随之增加。此外，当跨深比小于10时，采用欧拉梁和瑞利梁理论求出的各阶频率，尤其是高阶频率，与有限元计算结果之间的误差较大，而采用铁木辛柯梁理论计算出的频率依然吻合良好，误差均在5%以内。

图4 跨深比改变时三种梁理论下悬臂梁的固有频率计算结果

2.3 不同梁理论之间的对比

图5展示了梯度指数k=0.5在不同阶数时，不同梁理论所给出的固有频率计算结果。由图5可以看出，对于短粗梁(跨高比<20)，欧拉梁所给出的固有频率预测结果最大，瑞利梁次之，铁木辛柯梁最小，表明同时考虑横截面剪切变形和转动惯量对弯曲振动的影响可以有效避免对短粗梁固有频率的过分高估，且后者对固有频率的影响明显低于前者，因此铁木辛柯梁理论更适用于短粗梁的振动分析。同时，当跨高比大于20时，梁变得非常细长，此时横截面剪切变形和转动惯量对弯曲振动的影响甚微，从而三种梁理论所给出的预测结果非常接近。

图5 不同跨深比下不同梁理论计算的固有频率计算结果

3 结 论

(1)对于功能梯度悬臂梁而言，计算固有频率时应当根据梁的尺寸来选用合适的理论。对于短粗梁，由于欧拉梁和瑞利梁理论忽略了剪切变形对梁弯曲振动的影响，从而在一定程度上过高估计了梁的固有频率，相应的适用性明显低于铁木辛柯梁；当梁非常细长时(跨深比超过20)，横截面剪切变形和转动惯量对弯曲振动的影响甚微，从而三种梁理论所给出的预测结果非常接近。

(2)梯度分布指数k在0～5之间变化时，材料性能参数分布形式的变化非常显著，进而导致相应梁的固有频率发生较大变化，可通过改变材料性质的梯度分布来调节固有频率，从而避免目标阶的共振问题。