新型五轴龙门式混联机床的运动学分析∗∗

覃才友 黄 娟 李小汝

(①四川省高温合金切削工艺技术工程实验室，四川德阳618000；②四川工程职业技术学院，四川德阳618000)

混联机床概念的提出，源于上世纪90年代，因其 整合了串、并联机构、传统机床和机器人技术，使得混联机床具备了传统机床以及串联机构的大工作空间、灵活传动等特性，也兼并了并联机构刚度/质量比大、加工自由度易耦合等特性；与此同时还有效地避免了两者诸多缺点[1-2]，且混联机床在实际应用于航空航天领域中的异形曲面、汽车轮廓面等复杂型面的加工中，优点尤为突出。现广泛受到各国的青睐。混联机床也是今后制造领域的重要发展方向[3]。

截至目前，国内外制造业中已有一大批混联机床，并已成功量产化。其中国外最具代表性的:Tricept机床[4-5]，由Neumann提出并由瑞典 Neos Robotic公司将其量产化，该混联机床可完成3T2R运动共五轴联动，其中并联模块可完成2R1T运动；Huang等[6]提出一种五轴联动的Bicept机床，该机床优势在于装配了可移动滑台，增大了加工范围，适用于大型飞机零部件的加工；Adept Technology公司开发的五轴联动Adept Quattro混联机床[7]，也具备输出2R3T运动的加工能力，主要优势在于复杂曲面的制造和加工。国内研究中，具有代表性的为齐齐哈尔第二机床厂和清华大学共同研制的NXZ24龙门式五轴联动混联机床[8]；GAO等[9]提出并设计出一种有三自由度并联机构结合二自由度串联机构组合而成的五轴联动混联机床，该机床性能与结构与NXZ24类似。

本文基于Huang等提出的Bicept混联机床的构型，结合并联机构设计中的较为常用的方位特征集(POC)[10]方法和支链构造法[11]，并参考黄真[12]对3-RPS构型的并联机构的研究成果，提出一种五轴联动龙门式混联机床，主要优势在于能适应大尺寸复杂型面的加工。首先，对该机床加工运动的实现和原理进行了详细说明，结合串、并联模块实现功能将机床自由度解耦，为运动学分析奠定基础；其次，主要对并联模块中的3-RPS机构进行运动学分析，并结合支链的杆长条件，以及串、并模块自由度解耦结果建立机床运动学模型。并假设待加工工件曲面方程，通过自由度解耦的方法，求得刀具加工点的自由度驱动情况，并结合机床运动学模型求解得到最终驱动端所需的位移、速度输入量，实现加工过程的仿真。最后，结合Matlab，绘制待加工曲面以及驱动端位移、速度驱动量变化曲线；总结出该机床具有良好的运动学特性以及良好的加工自由度解耦性，为后续进一步开发和研究该类型机床具有一定的指导意义。

1 机床结构介绍

混联机床集串、并机构、传统机床、机器人技术于一体，具有诸多优点；最终加工过程在于完成刀尖点多自由度的耦合输出；考虑到机床加工过程中，串联机构比较善于完成工件的直线位移切削，故设计过程中，考虑让并联机构使刀具完成转动切削，最终将二者结合完成对工件的直线、转动耦合的切削加工过程。

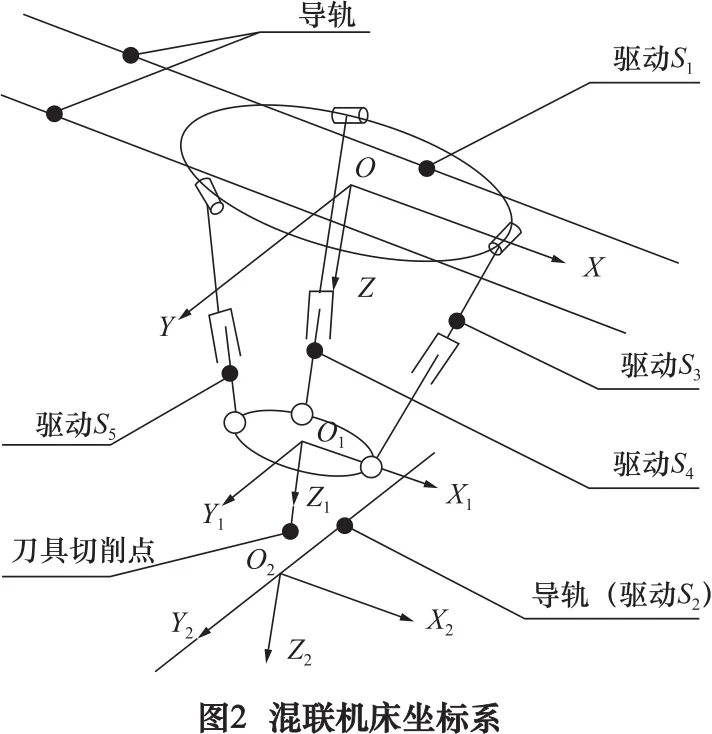
本文提出的新型龙门式五轴联动混联机床如图1所示，其中主要由两大部分组成，分别为串联模块和并联模块。具体原理及加工的实现如下:

串联模块:包括部件1、5；部件1可实现整体并联模块的X方向平移，即可完成工件X方向平移切削；部件5为滑台，可使工件完成沿Y轴平移运动，即可完成工件Y方向平移切削。

并联模块:包含部件 2、3、6。该模块主要为3-PRS并联机构，且在动平台上安装主轴电动机，完成整体构型。该模块主要负责完成刀具Z轴直线、绕X、Y轴转动，最终完成对工件的切削运动。

综合分析，该龙门式混联机床具体可实现工件X、Y、Z直线切削以及绕X、Y轴转动切削运动。

2 混联机床运动学分析

考虑工件的加工过程，首先通过由计算机读取待加工模型的数学信息，完成及规划工件加工过程中的走刀路径，最终将数学模型通过计算机输入控制端，通过算法，转化为最终驱动端的进给量，完成整个加工过程。

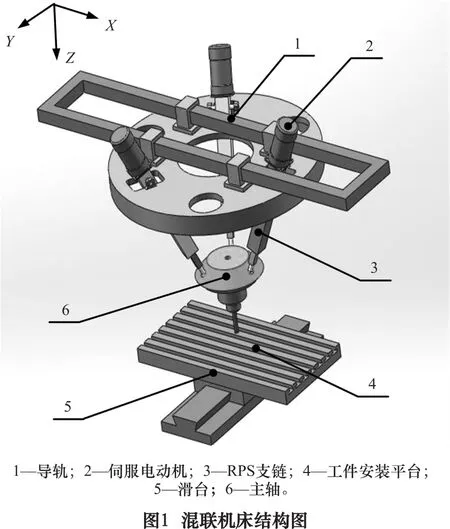
为便于对机床的加工过程中的运动学进行分析，对机床整体结构进行简化，并建立动、静坐标系。机床坐标系如图2所示。

图2中:O-XYZ为基座坐标系，后续加工信息完全参考于该坐标系；O1-X1Y1Z1为主轴质心坐标系；O2-X2Y2Z2为滑台坐标系；初始状态下三组坐标系Z方向完全重合。

为便于计算，现对机床中运动副在各自坐标系中坐标进行赋值，如:

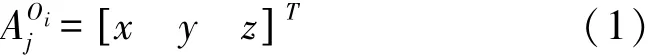
式中:A为运动副类型，本文为 S(球面副)、P(移动副)、R(转动副)；Oi为对应坐标系下的原点符号；j为第j个A副，当运动副相同时，代表驱动Si所对应的那个运动副。

图2中驱动Si对应第i个驱动自由度的输入。转动副所处坐标O-XYZ中，规定3个转动副处同一个大圆上，半径为r0。同理，球面副所处坐标系O1-X1Y1Z1中，设定所处半径为r1。现对各个运动副坐标赋值如下:

转动副坐标(O-XYZ坐标系中):

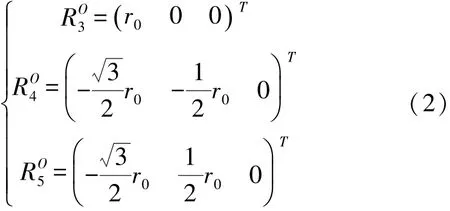
球面副坐标(O1-X1Y1Z1坐标系中):

本文首先通过构建机床运动学模型，并设定待加工曲面信息情况下，提取刀具走刀路径，最终求得5个驱动端驱动信息，最后结合Matlab进行仿真，并对机床加工中的运动学性能进行评估。本文主要研究技术路线如图3所示。

2.1 机床走刀路径提取及自由度解耦

考虑到机床加工过程中，规划好走刀路线后，选取路径中型值点，并通过插值点构建完整加工路线。选取路径中任意一点进行自由度解耦，如图4所示。

图4中，具体涉及初调和精调以达到加工位置。此过程并不代表为加工中的走刀线路，仅为便于自由度解耦而设定的数学求解方法。

图4a为待加工曲面，并提取走刀路线，图4b为刀尖点解耦情况分析。加工过程中经过点A坐标为(x0y0z0)。现将初始坐标解耦到平移切削量上的驱动1、2中，即为初调下该时刻驱动1、2位移驱动量(该时刻完成后，刀具轴线垂直于基座平面):

当刀具到达指定点后，需要调节刀具角度。此过程将进行一个Z轴平移和两个绕X、Y轴转动，最终使刀具轴线完全垂直于该点法平面，完成切削。此过程将再次对驱动端的驱动量产生累加。

具体累加计算如图4b所示；图中O1-X1Y1Z1为初调后主轴坐标系，O′1-X′1Y′1Z′1为该点最终加工位姿下主轴坐标系，且L1为刀尖点至主轴坐标系原点距离。

设定刀尖点路径在坐标系O-XYZ中的函数为:

且已知3个坐标信息构成待加工曲面，故一定满足函数关系:

那么微调过程各个自由度累加量结合式(5)、(6)可表示为:

则刀尖点从初始位置到达加工点A且到达加工位姿状态，机床所需总位移驱动为:

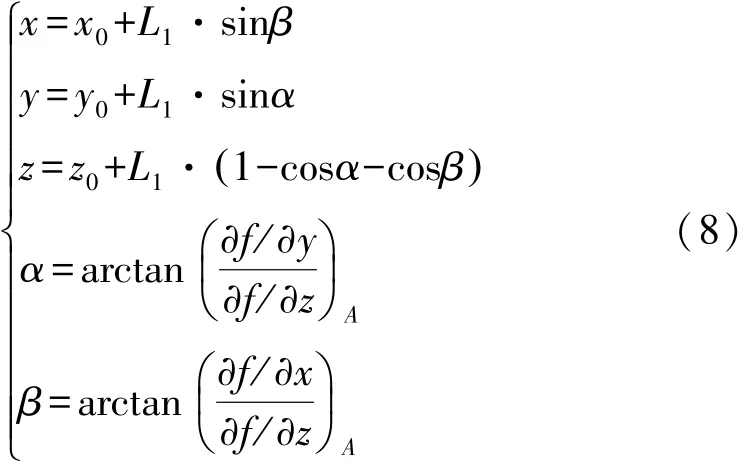
式中:α、β分别为主轴绕坐标系O1-X1Y1Z1的X、Y轴转动角度。

2.2 并联模块运动解耦

由于式(8)仅仅表示机床并、串模块在加工过程中所需完成的自由度分配情况，需要完全求解驱动端Si的具体直线驱动，还需对并联模块中提供的加工参数z、α、β()进一步求解；其中串联模块较为简单，且为直线驱动，则联立式(4)、(8)有:

进一步对参数(z、α、β)到参数(S3、S4、S5)做如下代换计算。

已知并联机构做运动学分析过程中的坐标变换矩阵为

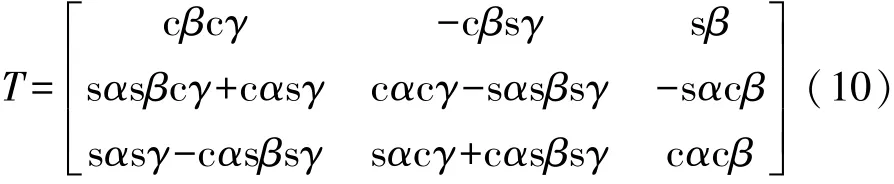
式中:sα 为 sinα；cα 为 cosα，依此类推 sβ、cβ、sγ、cγ 为β、γ的正弦、余弦；γ为绕Z轴转动角度。由于并联模块不具γ转动自由度，故计算中γ将始终作为常数0处理即可。

联立坐标系O-XYZ和O1-X1Y1Z1以及各运动副坐标(式(2)、(3))，任意时刻下并联模块3条驱动支链的杆长矢量可表示为:

式中:li为第i根支链杆长矢量(转动副到球面副位置矢量)，i＝3、4、5。

进一步对式(11)进行矢量求模运算，求解得到最终驱动位移 (S3、S4、S5)为:

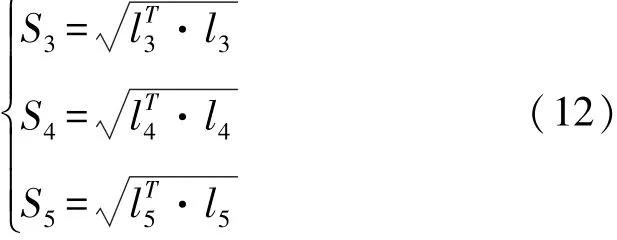
最终联立式(2)～(12)，求得，在已知曲面加工参数情况下，为完成加工过程，五个驱动端的位移输入情况为式(13)所示:

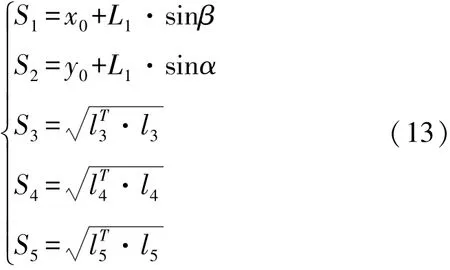
3 数值计算及仿真

3.1 加工型面设定

为演示加工过程中，已知走刀线路情况下，驱动位移的响应情况，现随意设定待加工型面(如图5所示)方程为:

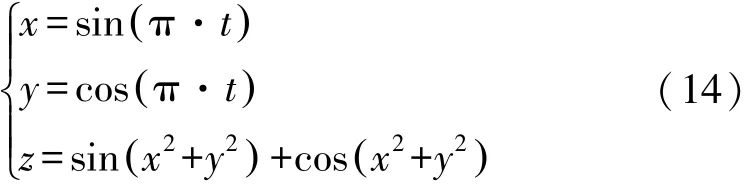
对待加工型面进行拟合，并选取图中任意一条路线作为走刀路径，为准确预测及观察驱动端运动情况，设定两条走刀路径，分别选取x＝0.5和x＝0.2时，所截得的曲线为加工路径，具体如图5所示。

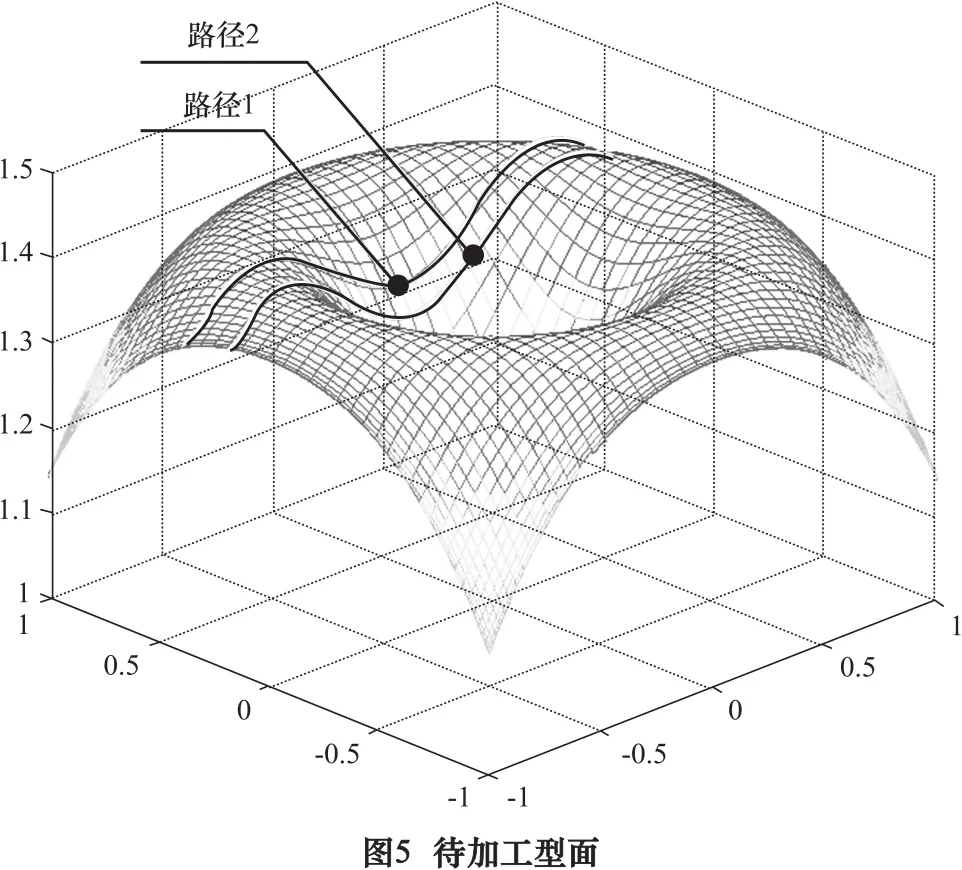
结合式(8)和(14)，可求解得到机床在图5中的两条走刀路径，任意时刻的切削自由度分配如式(15)、(16)所示。其中式(15)为x＝0.5时(路径1)加工参数，式(16)为x＝0.2时(路径2)加工参数。

式中:t为加工路径所需走刀时间。

式(15)、(16)表示为:在已知机床加工走刀路径的情况下，刀具及刀尖点所需完成的位姿参数，且为五维参数，分别为三维直线切削参数和两维转动切削参数，最终通过式(12)以及式(13)求解得到每个驱动Si的位移驱动值，完成机床加工过程的驱动端数值模拟。

3.2 机床结构参数及数值计算结果

已知机构学分析中，等比例缩放机构尺寸，机构整体的运动学性能不变，故在机床参数设计过程中；且参考现有类似机床尺寸，对本文混联机床进行尺寸等比例缩小后具体如表1。

表1 机床主要尺寸参数表 m

最后将表1中设定参数代入推导过程，并结合待加工曲面信息及走刀路径，对机床走刀过程中驱动端位移输入进行数值计算，其具体计算结果如图6所示。

对比两组仿真结果，首先分析串联模块端(驱动S1、S2)可以看出:

虽然走刀路线沿Y轴平移，但由于复杂型面切平面法线方向会对整体刀具的位姿X方向平移产生累加，基本可以看出t＝0.5 s和t＝1.5 s时刻，累积值最大，该时刻下位移主要由于刀具轴线绕 Y轴转动产生。

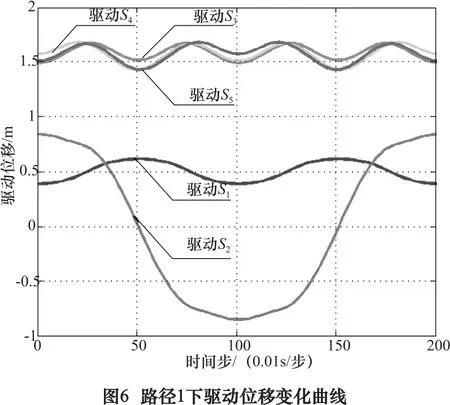
驱动S2曲线可以看出，时间t＝1.0 s达到极值。分析此时已经完成加工路径的走刀，故产生极值。注意到t＝0.5 s时刻，曲线变化速率较快，即为此时刻附近驱动端转速输入要求较高。

并联模块端(驱动 S3、S4、S5)可以看出:

对比两种情况分析，并联模块3个驱动支链杆长均值在1.5左右，由于整体采用对称结构，故输入位移驱动几乎相同或者稍有相位的延迟，极值几乎相等，且极值相互交替出现，极值差距范围不大，路径1下极值差距约为0.25，路径2下极值差距约为0.5左右；可以知道随着异形曲面的切线斜率的增加，加工完成所需的驱动范围加大。

综合理论推导结果、假定的曲面信息以及数值仿真结果，可总结该龙门式混联机床具有以下特点:

(1)由于篇幅关系，只对混联机床进行了一个曲面下两条走刀路径的仿真，其结果表明:完成走刀过程中，主要直线驱动位移由串联模块承担，也发挥了串联机构在完成平移运动中相对于并联机构的优势；且观察到并联模块驱动位移整体波动值较小，在控制过程以及算法的实现容易做到更精确；表明该机床整合了串联机构(运动范围大)、并联机构(控制精确)的优点。

(2)分析该机床，整体属于龙门式构型，其中串联模块作为基座，及其传统机床基座稳定性高的优势，配置高精度导轨，可完成机床高精度加工；并联模块采用对称3-RPS构型，保证了整体的刚度值，增加了一定的结构稳定性，为重载加工的实现奠定基础；且分析该模块位移驱动曲线较为平缓，无突变等情况，进一步发挥了并联机构运动平稳性的优点。

(3)该混联机床相对于其他混联机床，结构改变在于将串联模块完全解开，其中一个串联模块自由度直接配置于并联模块上，优点在于可使整个并联模块按照解耦自由运动，减少了大质量工件在加工运动过程中对刀具切削点的刚性冲击，增加刀具的使用寿命。

4 结语

(1)本文通过参考Bicept混联机床的构型，以及对3-RPS构型的并联机构的研究，提出一种五轴联动龙门式混联机床，并分析了该机床实现加工过程的原理以及该过程的自由度解耦等情况。其中机床主要由串、并联模块组成，串联模块完成待加工工件的Y轴平移以及并联模块整体的X轴方向平移；并联模块完成对刀具的Z轴平移以及绕X、Y轴的转动，最终实现五轴联动加工过程。

(2)对加工过程中的自由度解耦进行了详细分析，首先通过设定加工型面，然后提取走刀路径，并通过坐标变换等，将路径解耦为刀具以及基座5个独立的自由度驱动，最终结合串、并联机构性质，求解每个驱动端完成该路径所需的位移驱动情况，并进行数值仿真；对机床整体运动性能进行了评估。

(3)设定两条走刀路径下进行Matlab数值仿真结果表明，该机床良好地集齐了串、并联机构的优势，将各机构擅长的运动方式完全用于机床加工的驱动中，物尽其用，各自发挥了各自的优点。

(4)综合分析，该混联机床具有良好的驱动端位移分配性能，使大范围平移由串联模块提供，小范围、高精度由并联模块提供，证明整体的结构设计的合理性，从仿真结果依旧可以看出整体运动的平稳性。为此，该混联机床为今后机床领域的研究和开发提供了新的构型以及一定理论基础。