基于散布误差分析的改进射击成绩评定模型∗

王 蕾 刘 洋 周德超

（海军工程大学兵器工程学院 武汉 430033）

1 引言

舰炮射击检靶误差，直接影响着部队射击训练成绩的评定。如何保证射击成绩正确评估，提高射击成绩对检靶误差的容错率，是一个值得研究的课题。

文献［1］研究了弹着点均匀散布对圆目标毁伤概率的计算，提供了弹着均匀散布的模型构建方法。文献［2］研究了弹着点离散化方法，文献［3～4］研究了弹着点的椭圆散布，丰富了弹着散布的模型集。文献［5～7］针对各种具体情况下的落点散布，给出了各种武器的弹着散布模型。进一步，文献［8～9］根据落点散布计算了导弹抓取和攻击正确目标的概率。文献［10］则设计了基于声定位的自动检靶系统，在实验中国检验了系统检靶精度。以上资料对弹着散布和检靶误差进行了研究，但是并没有从射击成绩评定的角度，研究弹着散布和检靶误差的影响。本文从分析弹着散布圆的角度入手，建立一个新的射击成绩评定模型。梯度设置检靶误差，利用统计模拟法［11～16］模拟多个弹着场景进行成绩评定，进而分析各种情况下检靶误差对射击成绩评定的影响。

2 典型成绩评定模型

2.1 弹着散布分析

为了研究弹着散布，选择平面直角坐标系xOz，如图1所示。xOz在水平面内，原点O与散布中心重合，x轴与射击方向一致，z轴与射击方向相垂直的横向方向一致。射击诸元不变，在相同条件下连续发射若干发弹丸，各发射弹丸的弹道各不相同，形成一个弹道束，这种现象称为弹道散布。θ0是射角，是弹道的初角。

图1 弹着散布

在弹道束中，有一条未受任何散布影响的弹道，称之为中央弹道或平均弹道，它是与火炮射击诸元相对应的，与中央弹道对应的弹着点称为散布中心。把弹着点相对散布中心的偏差量称为弹道散布误差，它在水平面x轴、z轴上的投影Δx0和Δz0分别称为弹着距离散布误差和弹着方向散布误差，见图1。

海上射击训练时，一般对拖靶进行射击，关键是判定每一发弹的弹着是否算作有效弹着。图2描述的是拖靶的投影矩形，其中θ是弹道落角。

图2 拖靶矩形投影

绿色矩形代表拖靶，高度为H，宽度为W，红色部分是拖靶沿着弹道落角的投影，H1是投影区域的长度。

由上模型可知，弹着点围绕散布中心无序分布，因此在舰炮和拖靶连线方向上近端和远端均有弹着点。在判定射击成绩时，近端的弹着点视为无效弹着点，远端的弹着点视为有效弹着点。当当次射击共发射N0发炮弹，而通过检靶共得到N发有效弹着点，那么本次射击的有效率为

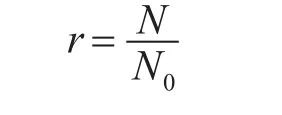
设置判定阈值r1＞r2＞r3＞0，当次射击成绩判定规则如下：

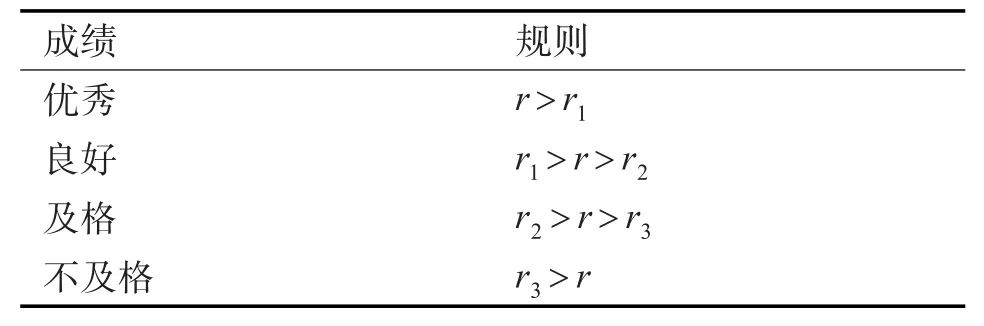
2.2 合理性和不足分析

典型成绩评定模型将弹着分为远弹弹着和近弹弹着，其中将落入拖靶投影矩形内的远弹弹着视为有限弹着，并用于计算当次射击成绩。由于确定有效弹着的方法较为简单，同时充分考虑距离散布，该模型在评估射击成绩方面是合理的。

同时，由于确定有效弹着的方法较为简单，未充分考虑弹着点距离散布和方向散布，与概率散布误差之间的关系，较大的检靶误差会导致真实有效弹着的确定存在不确定性，并最终导致射击成绩的误判。

3 基于散布误差分析的改进射击成绩评定模型

设Ex0为弹着距离散布误差Δx的概率误差，Ez0为弹着方向散布误差Δz的概率误差，ρ为正态常数。弹着散布误差的二维正态分布密度函数φ(x，z)的函数表达式为

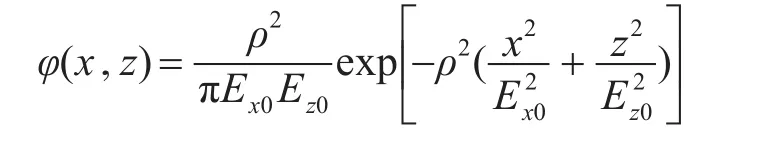
典型成绩评定模型的炮弹落点有效判定区域为投影矩形，假设散布中心与投影矩形中心重合，其单发命中概率为P0为

由于二维正态分布密度函数φ(x，z)的分布密度相等的点的轨迹应满足椭圆：

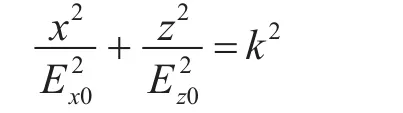
其中k为常数，当k=1时为单位散步椭圆，即此时概率密度函数φ(x，z)对椭圆面积区域积分所得的概率为1/2。设概率密度函数φ(x，z)对椭圆面积区域积分的积分值为 P1，寻找k的值，使得φ(x，z)对椭圆区域内积分的概率值与P0相等。

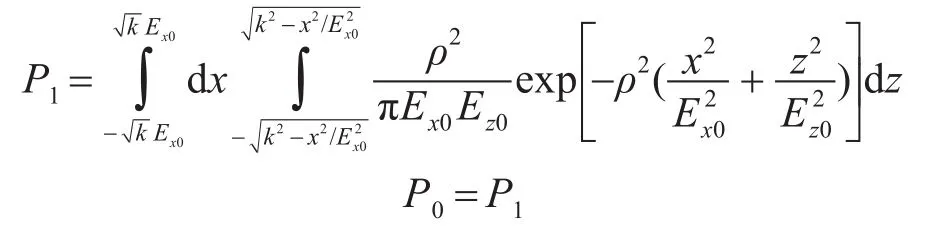
4 统计模拟法的应用

4.1 统计模拟法基本原理

统计模拟法又称统计试验法，它是一种运用数理统计理论，近似求解各种实际问题的方法。其主要思想是为了求解某个问题，首先建立一个概率模型，使它的概率特征等于问题的数值解；然后对模型进行最忌抽样试验，经过统计计算，以符合精度要求的统计估计值作为问题的近似解。简言之，统计模拟法的基本思想是通过随机抽样与统计计算来确定包含各种复杂因素的概率特征。

应用统计模拟法求解某一问题，其计算是比较简单的，其模拟过程也比较灵活，统计模拟法适用于解决用解析法难以解决，甚至是不可能解决的一些问题，如本文中估计检靶误差对射击成绩评定的影响。

4.2 统计模拟法迭代次数的确定

统计模拟法的精确度是一个很重要的问题，因为精确度实际上决定了统计模拟发的适用程度。由于统计模拟法是以统计估计值近似所求实际问题数值解的，因此，统计模拟精确度适合随机抽样的试验次数密切相关的。即精确度要求越高，需要的抽样次数就越多；但是抽样次数无限增加会增加计算时间，甚至导致对统计模拟法的拒绝使用。

精确度ε和统计模拟法的试验次数n有着直接的关系，其表达式如下：

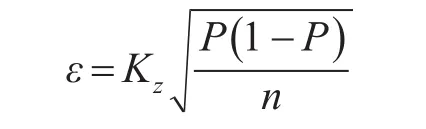
变换以上形式，则得精确度为ε时需要的模拟次数n，即

其中，Kz是置信系数。通常情况下，若给定置信系数为2.0，此时的对应的置信概率已经达到95.4%，可以认为以统计估计值Pˉ近似代替事件概率P的可靠程度相当高。此时上式可以简化为

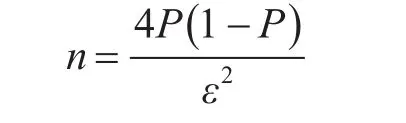
5 仿真实验和分析

5.1 弹着散布场景生成

根据靶标大小，建立坐标系如下，靶幅为图中实线部分：

图3 弹着散布效果图

假设射弹散布中心与靶标中心重合，根据平均射距可以得到一倍概率误差。依据正态分布概率，在)区间的面积为99.73%。即模拟弹着在距离靶标中心三倍概率误差范围之外是没有意义的。因此，在距离偏差和方向偏差上，20枚弹着均落在距离靶标中心三倍概率误差范围内。

5.2 检靶误差影响仿真实验

假设某型舰炮射击靶标高度15m，宽度20m，查阅射表得到在指定射击距离时，弹丸落角为15°，标准距离散布35m，标准方向散布5m。假设人工检靶误差的均方差分别为3m、6m、9m。判定阈值r1=0.4，r2=0.3，r3=0.2，令仿真射击时，弹丸散布误差的分布中心为靶标中心。定义κ为射击散布系数，射击时弹着距离散布误差Δx的概率误差为κEx0，弹着距离散布误差Δz的概率误差为κEz0。

分别取κ为1.5、2.5、3.5，使用统计模拟法计算引入检靶误差后，两种方法计算成绩时评分发生改变的概率，图标中黑色表示传统方法，灰色表示改

拟定20枚弹的真实弹着，分为试射近弹4发、试射远弹4发、效力射12发。考虑模型主要检验射击成绩评定结果对检靶散布误差的敏感性，因此在评估成绩时不再将试射弹着与效力射弹着进行区分。进后的方法。

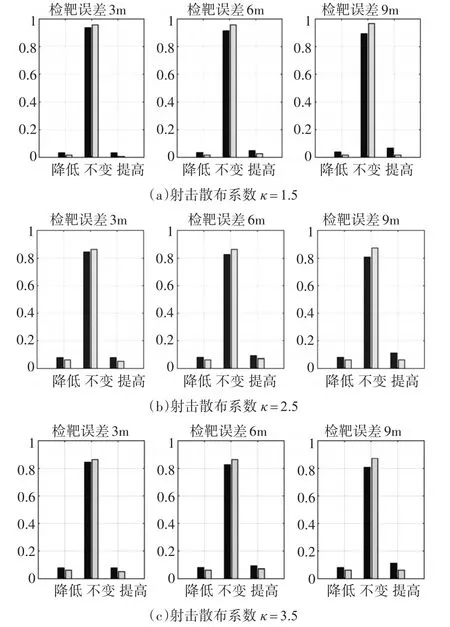
图4 不同射击散布，不同检靶误差下检靶成绩

分析上图，可以得到如下现象：

1）从图4（a）中可以得到在检靶误差小于10m时，模型改进前后正确评估射击成绩的概率均在90以上，仿真中验证了射击成绩评定模型设计的合理性。同时改进模型提高了正确评估射击成绩的概率，说明改进后的算法在实际应用中更加有效。

2）纵向对比，图4（b）和图4（c）正确输出射击成绩的概率明显低于图4（a），说明射击散布系数增大，会导致射击成绩评估不准确。

3）从各图评分变化时的情况看，当射击成绩评估不正确时，评分提高的概率普遍低于评分降低的概率，反映在实际训练中是射击成绩优秀率降低。

进一步分析可知：

假设在角分辨率误差不变，射击散布大意味着弹着点距离散布中心较远，导致距离误差大，因此增大了检靶误差，并最终影响了射击成绩的判断。

改进的模型提高了正确输出射击成绩的概率，关键在于原模型未充分考虑概率散布误差，而改进后的模型使用了椭圆散布概率误差来判断有效弹着，在探索弹着散布规律方面更加符合实际情况。

由于使用了概率圆的概念，假设可能的检靶点分布在真实落点的周围，检靶点可能落在散布中心的近端，也可能落在散布中心的远端。但是最大的检靶误差是相同的，三维正态分布投影在二维平面时显然均值中心附近更加密集，因此相同的检靶误差，在散布中心近端跨越的层级更多。当跨越了设定的阈值时，成绩将提高一个层次。因此评分提高的概率更大。

6 结语

本文针对经典射击成绩评定迷行存在的误判概率较高的问题，采用等概率转换的方法，引入了椭圆散布概率模型。实验结果显示，改进后的模型在正确评估射击成绩方面表现更优。