Buck变换器级联系统直流母线电压稳定控制策略研究∗

马佳睿 穆 琳

（1.91404部队 秦皇岛 066000）（2.92956部队 大连 116041）

1 引言

直流母线稳定性问题是级联系统无法回避的一个问题。独立运行时都能保持稳定的子系统级联后可能会导致整个系统的不稳定［1～4］，可以通过增加滤波电容改善输入电压波形。但是这种硬件改进方法降低了功率密度增加了系统成本。根据电源的输出阻抗和变换器闭环输入阻抗比，即最小环路增益，基于文献［5］提出的ESAC准则，只要使最小环路增益不进入禁止区域就能够使系统稳定。文章提出输入电压前馈制策略及其控制器的设计方法，显著改善了母线电压的动态性能，有利于提高系统功率密度，降低成本，增加系统灵活性。

2 Buck型级联系统建模与分析

2.1 Buck型级联系统数学模型

图1所示为所研究的Buck级联系统电路图。电源为非理想电源具有内阻ZS，前级变换器输入输出阻抗分别为Zin和Zout，后级变换器闭环输入阻抗为ZL。

对于图1所示前级Buck电路，当IGBT导通时有：

对式（1）、（2）、（3）、（4）取开关周期平均算子得：

式中“^”表示扰动量，IL、Vg、Uo、D、Io表示直流分量。将式（7）、（8）、（9）、（10）、（11）带入式（5）、（6）、（7）、（8），并略去二次交流量可以得到由占空比到输出的开环传递函数：

同理可以得到Buck电路的全部开环传递函。表1给出了单个Buck电路的全部开环传递函数。图2为根据Buck型级联电路系统得出的控制系统框图。其中ZL为后级变换器的闭环输入阻抗。

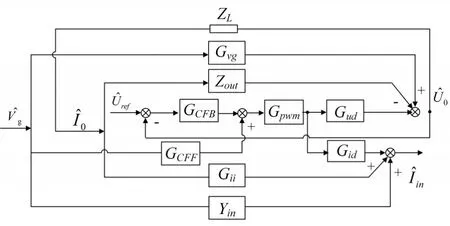
图2 Buck型级联系统控制框图

根据图2容易得到在无前馈控制器时前级Buck变换器输入导纳为

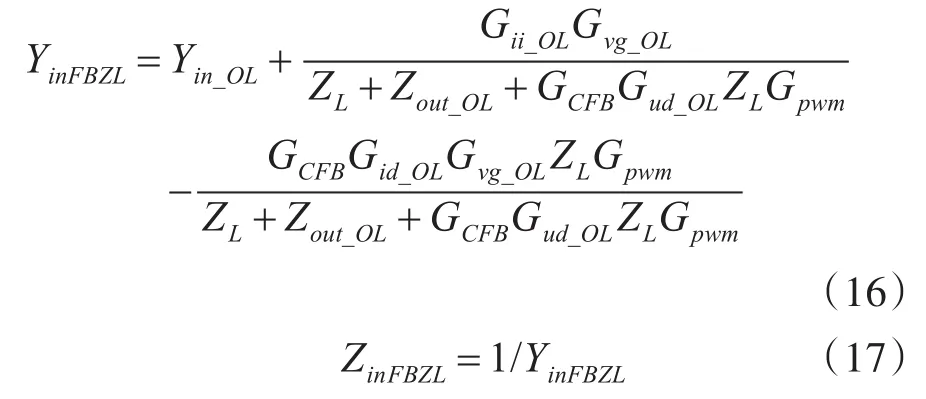
有前馈控制器时前级Buck变换器输入导纳为

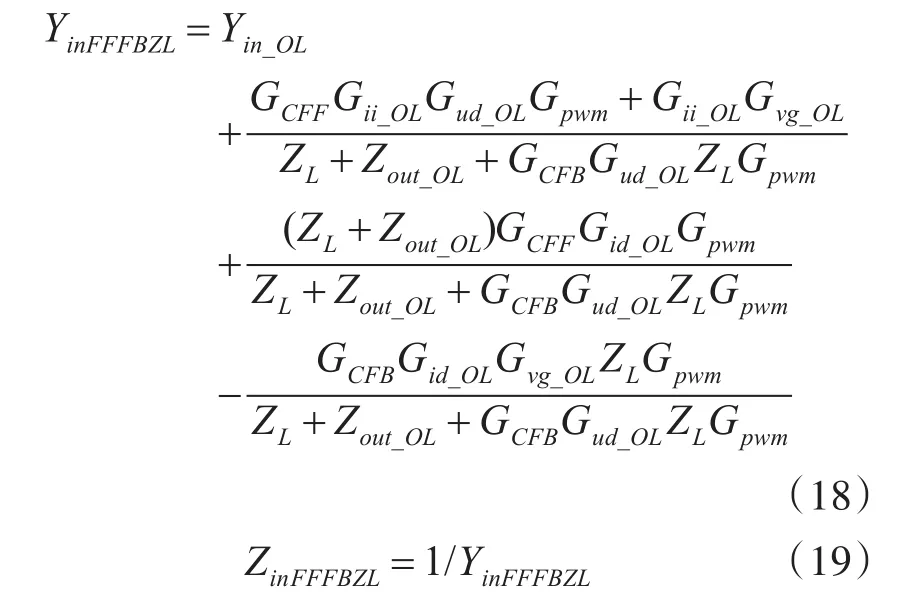
其中：

根据Thévenin定理，可以得到电源输出阻抗为

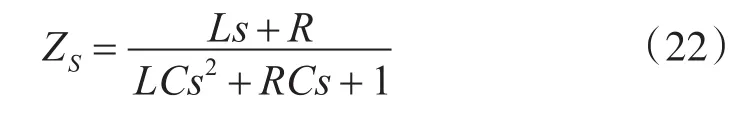
2.2 Buck型级联系统仿真与分析

系统各部分电路参数如下：

R0=0.05Ω、L0=0.1mH、C0=2000μF、R1=4Ω、L1=1mH、C1=1000μF、R2=4、L2=1mH、C2=1000μF、Vg=300V。给出前级和后级变换器的反馈控制器分别为

则前级和后级Buck变换器的开环传递函数分别为

图3为校正后前级Buck变换器和后级Buck变换器的开环传递函数Bode图，可以看出用式（23）和式（24）校正后系统具有约60°的相位裕度和较大的幅值裕度。系统带宽约为1kHz，具有较快响应速度。

图3 校正后系统开环传递函数Bode图

图4 、图5所示为无前馈时电源输出阻抗、变换器输入阻抗Bode图和ZS/Zin的Nyquist图。通过图4可以看出在356Hz频率点附近，电源输出阻抗和变换器输入阻抗幅值比较接近，电源输出阻抗和变换器输入阻抗会相互影响，降低系统稳定性。从图5可以看出在356Hz频率点附近系统的最小环路增益产生较大的相位滞后，幅值为-4dB，接近（-1，j0）点，系统稳定性较差，系统输入电压将产生频率约为356Hz的周期性振荡。图6、图7为无前馈控制时级联Buck系统输出电流仿真波形和电压仿真波形。

图4 引入前馈控制前电源和级联Buck变换器输入阻抗Bode图

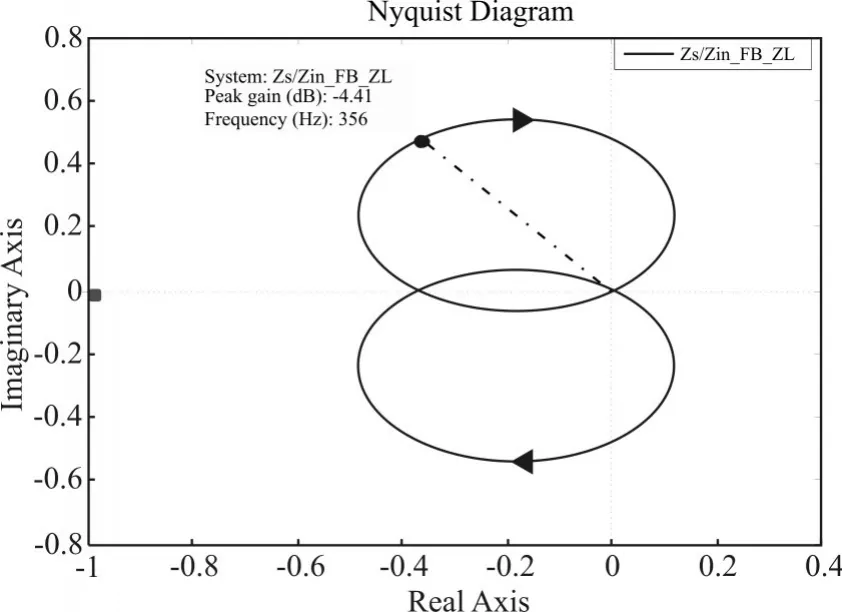
图5 无前馈时级联Buck系统最小环路增益Nyquist图

图6 后级Buck输出电流仿真波形

如图7、图8所示，无前馈控制器时，系统输入电压存在波动，0.2s时刻后级Buck负载电流由25A阶跃至125A时，系统输入电压波动幅度明显增大，前级Buck输出电压也出现波动。图8级联Buck系统电压仿真波形局部放大图，由图可知输入电压波动频率约为356Hz，与前面分析一致。

为了减弱电源输出阻抗ZS与级联系统输入阻抗Zin的相互影响，增加系统稳定性，引入前馈控制器。根据图4与图5，引入前馈控制基于三个出发点：

1）提高系统最小环路增益ZS/Zin在356Hz频率点附近的相位裕度。

2）提高系统最小环路增益ZS/Zin在356Hz频率点附近的幅值裕度。

3）同时提高系统最小环路增益ZS/Zin在356Hz频率点附近的相位裕度和幅值裕度。

在此给出系统所用前馈控制器：

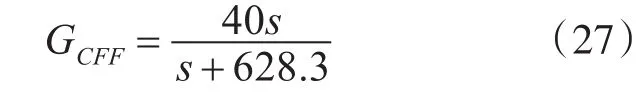
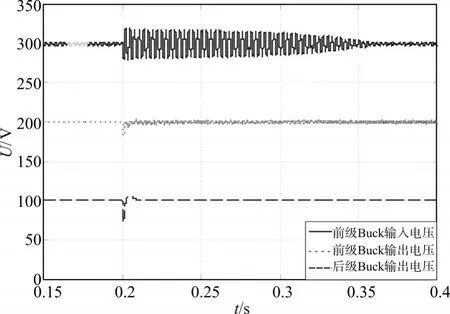
图7 级联Buck系统输出电压仿真波形

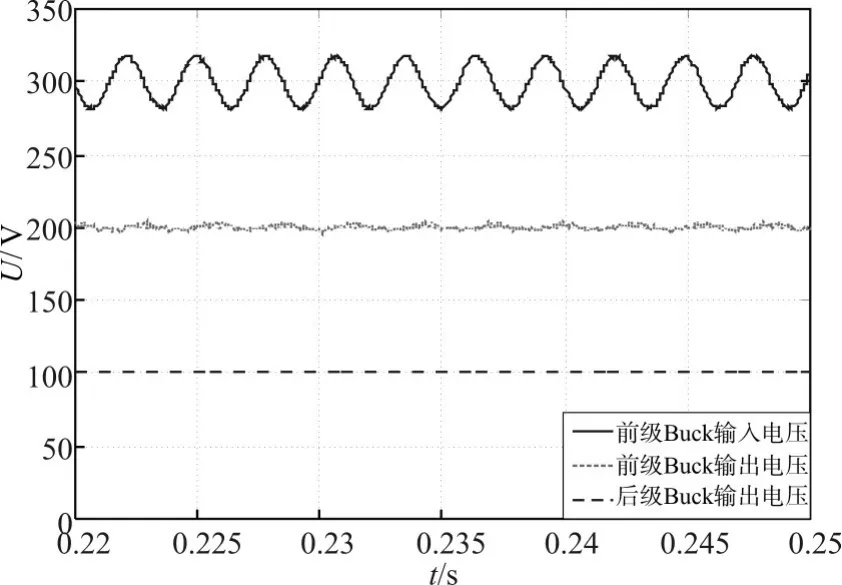
图8 级联Buck系统电压仿真波形局部放大图

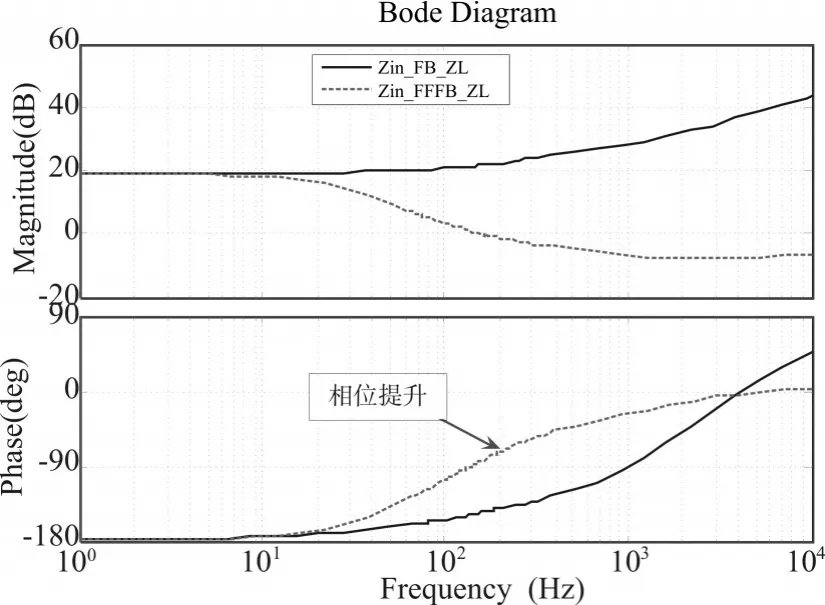
图9 引入前馈控制前后级联Buck变换器输入阻抗Bode图

图9 为引入前馈控制器前后级联Buck变换器输入阻抗Bode图。从图中可以清楚看到引入前馈控制后输入阻抗在356Hz频率点附近的相位裕度有明显提升，从而改善了系统动态性能。

图10 引入前馈控制前后级联Buck变换器最小环路增益抗Bode图

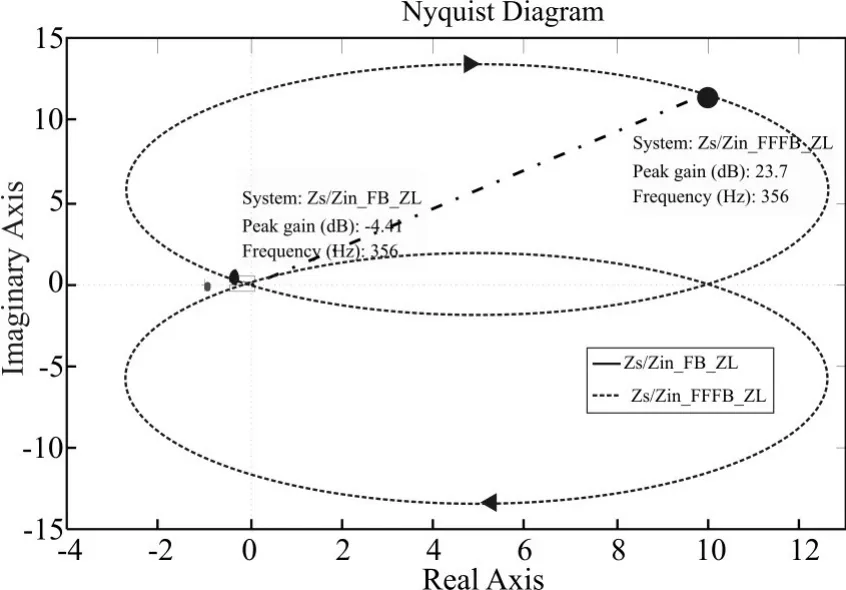
图11 引入前馈控制前后级联Buck变换器最小环路增益Nyquist图

图10 为引入前馈控制器前后级联Buck变换器最小环路增益Bode图。从图中可以清楚看到引入前馈控制后输入阻抗在356Hz频率点附近的相位裕度有明显提。图11为引入前馈控制器前后级联Buck变换器最小环路增益Nyquist特图，引入前馈控制后在356Hz频率点附近系统最小路环路增益位于第一象限，相位裕度和幅值裕度得到明显提升。从而能很好地抑制系统在356Hz频率点附近的周期性振荡。

图12 引入前馈控制后级联Buck变换器电压仿真波形

图12 为引入前馈控制后系统输出电压仿真波形。从图中可以看出引入前馈控制后当负载电流从25A阶跃至125A时系统动态特性有很大提高，振荡时间缩短，呈收敛振荡，增强了系统稳定性。

3 结语

本文采用小信号建模的方法，对级联型Buck电路建立了准确的数学模型，从理论上分析了系统产生周期性波动的原因在于电源输出阻抗和变换器输入阻抗在356Hz频率点附近幅值十分接近，系统最小环路增益幅值裕度和相位裕度很小，相互作用很强。通过Matlab进行时域仿真验证了理论分析的正确性。

为了抑制系统振荡，改善系统的动态特性提高系统稳定性，文章设计了前馈控制器，在理论上分析了前馈控制器的作用在于提高了变换器输入阻抗的相位裕度，从而使得系统最小环路增益在356Hz频率点附近的相位裕度和幅值裕度都得到了提升。需要说明的是前馈控制器的设计应注意两点：

1）前馈控制器的通带应该覆盖系统固有振荡频率点。

2）前馈控制器一般设计为高通滤波器，能为系统带来相位提升。

最后通过Matlab进行时域仿真，各输出波形较无前馈控制时都得到了明显改善，系统稳定性得到提高，验证了所设计的前馈控制器的有效性和理论分析的正确性。