匀变速直线运动的位移与时间的关系

文 凯

(天津市滨海新区大港油田第一中学 300450)

“匀变速直线运动的位移与时间的关系”这一知识点的学习十分重要，是高中物理学习的关键所在，这节课的重点内容是研究物体怎样进行匀变速直线运动的，在研究该内容的时候高中生一定要注意将物体的运动进行理想化和简单化，将摩擦力和阻力忽略不计，这样才能将这种运动研究的更加透彻.身为学生在解题的过程中一定要学会观察运动的变化图，同时还要记住匀变速直线运动的相关推导公式，最后通过列一元一次方程组的方式解决问题，这是这类问题的大体解决过程.

一、匀变速直线运动概述

匀变速直线运动的特征为加速度方向与初速度方向相同或相反，且固定不变.因此在匀加速直线运动中，速度为时间的一元一次函数，即速度v等于加速度a乘以时间t加上初速度v0，如下图.

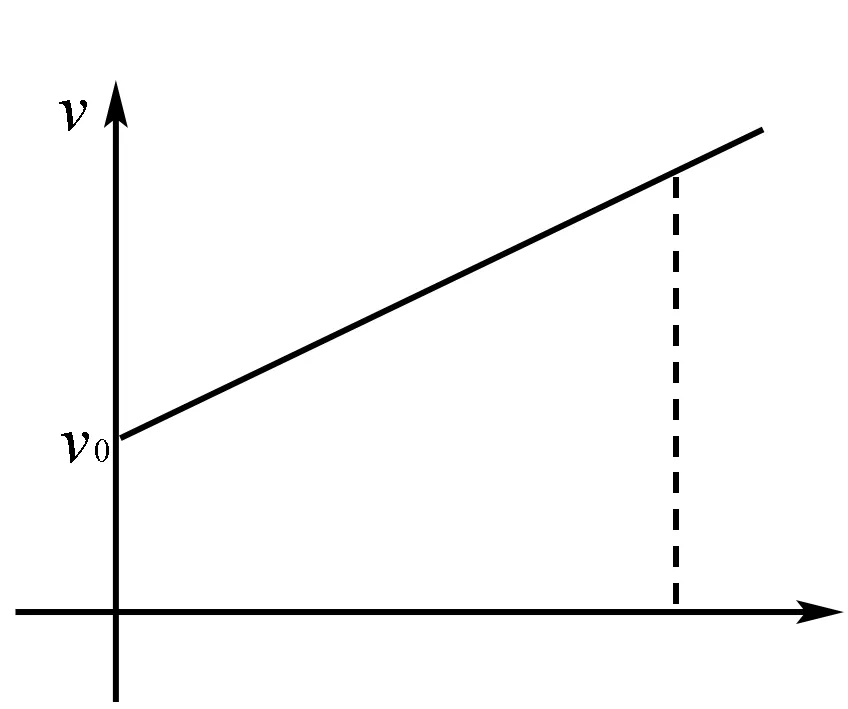
直线运动位移为速度v与时间t的乘积，因速度v随时间匀速变化，匀变速直线运动的位移为上图阴影部分面积，即为匀变速运动平均速度与时间的乘积，位移x=[(at+v0)+v0]/2×t=at2/2+v0t.过程中需要注意的是物体在进行匀变速直线运动的时候，必须要满足以下两个条件：

1.物体所受合外力不能为零，同时要保持不变.

2.物体运动中的初速度与其所受的合外力必须要保持在同一条直线上，同时运动方向始终保持不变.随着时间的增加，物体的速度逐渐提高，则表示物体在做匀加速直线运动，反之，物体在做匀减速直线运动.匀变速直线运动的位移公式为x=v0t+at2.

二、匀变速直线运动的位移与时间的关系

1.图像为一条直线

如果图像上显示出一条直线，且这条直线与t(时间)轴平行，从0-t的时间内，该条直线与t轴所形成的图形为矩形，随即可以算出它的面积为vt，此时物体所形成的面积就是物体移动的距离，我们可以通过图像清楚看到物体在做匀速直线运动，若将矩形面积记作x，则此时x=vt.在速度不变的情况下，矩形的面积会随着时间的增加发生增长，这个就是一个最简单的匀速运动方式.

2.图像为一条倾斜直线

如果x-t图像显示为倾斜的直线，则可以表明此时的物体正在做匀变速运动，这一时间内物体的移动速度和移动方向可以利用直线的斜度表示.对此，可以将物体的每一段运动看作匀速运动，过程中产斜线与时间轴形成的小矩形则为各段匀速直线运动的位移.如果根据图像的实际走向以及形成的矩形面积进行计算，可以发现矩形面积之和要小于匀变速直线运动在此时间中的实际位移.当物体在各个时间段不断减少时，通过两个图像的对比可以发现匀速直线运动位移与匀变速直线运动位移的差值会越来越小，最后图像会呈现出一个梯形，此时的梯形面积就是位移.匀变速直线运动公式为x=v0t+at2.

3.图像为一条抛物线

如果x-t图像显示为抛物线，此时物体的速度可以由该条抛物线上任意一点的切线斜率来表示，速度的实际方向由斜率的正负来表示，当物体从图像上t=0离开时，此时的抛物线体现的就是物体初速度位移与时间的变化规律，物体在运动一段时间后会逐渐开始进行此匀变速运动，在这样一个环境下，学生要注重对于物体初速度以及加速度的研究力度.

4.匀变速直线运动的特例

最为常见的匀变速直线运动特例，就是物体的自由落体运动，这是一种性质比较特殊的没有初速度的匀变速直线运动.

例如：果树上的水果成熟后就会自己掉落就属于自由落体运动，其初速度为0，加速度为g.在探讨自由落体运动时一定要忽略空气阻力的影响，因为只有在理想化条件下物体才能做自由落体运动，这时物体才能做匀加速直线运动，它的运动方向向下，加速度等于重力恒定不变为g，理想状态下g=9.8 m/s2

5.生活实例

学生要想将匀变速直线运动的位移与时间的关系了解的更加透彻，就需要寻找一些位移公式作为载体来了解相关理论知识，学生要将此知识与生活当中的物体运动联系在一起进行分析.

例如：赛车在静止的跑道上加速、火车移动等现象，通过与生活相结合能够促使学生对知识的理解和记忆.因此学生要学会从生活中找出例子，并将所学知识与生活进行联系，同时在结合图像的变化，学生就能对所学知识有更好的理解和认识.

综上所述，匀变速直线运动对于高中物理学习来说具有重要意义，在学习这一课时学生一定要将图像与生活进行有效的结合，这样有利于学生更好的掌握位移与时间的关系，从根本上扎实的掌握匀变速直线运动的相关知识，并能够将其灵活运用到实际学习和生活中.