全国卷解析几何专题考点分析及学生存在问题揭示

吴 攀

(福建省漳州市第三中学 363000)

数学科考试宗旨主要测试学生数学的“三基、五能、两意识”.其中三基包括：数学基础知识、基本技能和基本思想方法.五能包括：空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力.两意识包括：数学应用意识与创新意识.而解析几何内容突出考查学生的运算求解能力、数形结合思想、和将几何问题代数化的本质.下面我们通过对解析几何专题作简要研究分析，提出高考备考建议.

一、解析几何常考问题类型梳理

1.椭圆、双曲线或抛物线定义应用及特征量问题；2.求曲线或轨迹方程问题；3.最值问题；4.定点或定值问题；5.直线与圆锥曲线关系问题：弦长、中点、面积、对称、平行、垂直、夹角等；6.探索性问题：含参数问题、最值问题、存在性问题等.

二、试题特点

1.题型：题型结构比较稳定，选择题或填空题共2道、1道解答题，共3道题，分值为22分，占全卷约15%；椭圆、双曲线、抛物线三种曲线都有涉及.

2.难度：从近三年试题分析发现，解析几何试题的难度明显降低，18年解析几何大题从20题首次提前到19题，这是近几年首次.

3.试题基本不给坐标系和图形，对数形结合思想考查的要求较高，要求考生具备较强的几何与代数之间互化的能力.

4.在近三年的高考中，理科选择或填空题均考查到双曲线的相关知识，解答题都是以椭圆为背景；文科大题都是以抛物线为背景，小题都有椭圆，另一个小题常以圆为背景；对两个知识点的考查均体现较强的稳定性.

5.解答题中关注弦长、面积、角度、垂直等几何量的“代数”运算，试题常涉及算法的合理选择.

6.全国卷文理科解答题背景资料有时是相近的，甚至是同题(如2018年).

7.试题常渗透平几知识.

三、存在问题

1.缺乏科学严谨的作图习惯，充分用图能力弱

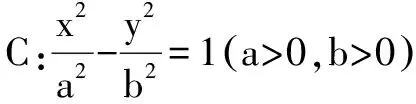
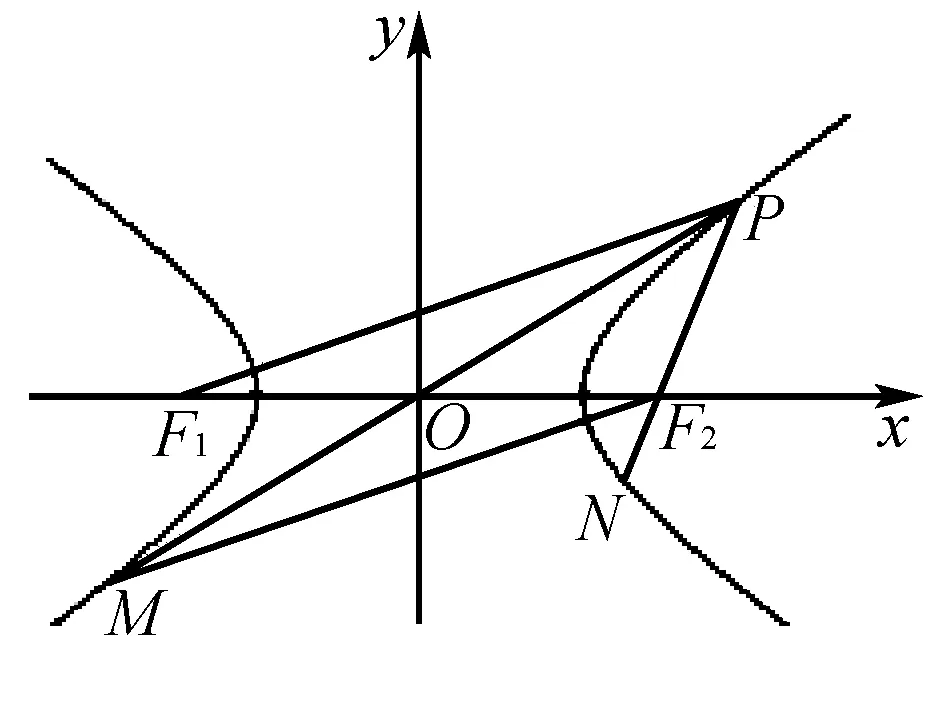
评析如图所示，如果没有科学规范的作图，又没有结合图形的对称性，学生将较难发现∠F1PF2=∠MF2N=60°，导致解题无法进行.

建议：1.教师在讲课时注意使用尺规规范作图，起到良好的示范作用.2.要求学生作图练习(包括立几中的锥体柱体).学生练习不给图形，要求学生自己作图.

2.缺乏对圆锥曲线定义的深刻理解，应用定义意识有待加强

例2 (2016全国Ⅰ卷理20)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1，0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E．(1)证明|EA|+|EB|为定值，并写出点E的轨迹方程．

评析学生未能从定义出发，研究题目中动点满足的不变几何关系，实现用简便方法将几何问题代数化.

建议：1.理清求轨迹问题的方法；2.通过方法的优劣比较，引导学生合理选择方法，优化解题方法；3.适当强调几何性质，加强课堂教学的严密性和条理性．

3.缺乏对几何问题代数化策略的深入研究

评析学生缺乏对几何问题代数化策略的深入研究，导致无从下手.其实，法一：可设A(x1,y1),B(x2,y2)，由于直线是过x轴上的定点，把直线投影到y轴后，可得线段AF与线段FB的投影也存在y1=-3y2这一关系，从而将几何关系坐标化，达到简化运算的目的.法二：也可通过椭圆的第二定义，将线段AF与线段FB的长度分别转化为A、B两点到准线的距离，再通过几何关系求解.

建议：训练学生规范作图，加强几何问题代数化研究，结合曲线的几何特征，尽量以简洁的代数形式呈现，从而实现问题的简化．

4.计算能力弱，即算法的合理选择意识弱，简化运算的意识待加强

例4 (2015全国Ⅱ卷理20)已知椭圆C:9x2+y2=m2(m>0)，直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．

(1)证明：直线OM的斜率与l的斜率的乘积为定值；

5.其他问题

从学生方面看，学生计算能力弱，即算法的合理选择意识弱；学生存在畏难怕繁情绪，缺少克服困难的信心和耐力.从教师方面看，课时紧张，教师不舍得花课时讲透题目；缺少归纳和学生弱点的针对性训练；缺少系统性总结反思和给学生积极的心理暗示.

只有找出问题才能更好地解决问题．我们在平时教学过程中，要善于引导学生充分利用图形，挖掘图形特征，利用图形转化几何关系．平时教学中应引导学生关注平面几何知识，特别是三角形的中位线、相似等条件的应用，常常能减少运算量．同时，在计算过程中，注意培养学生的整体代换思想，通过设而不求等方法简化运算．总之，解析几何专题学习既要注重基础和通性通法的掌握，又要注重培养学生理性思维和锲而不舍的学习品质，在教学中我们需要详略得当，扎实引导，层层突破.