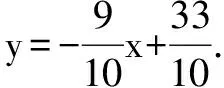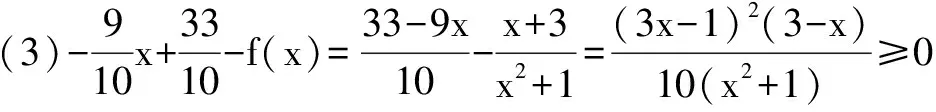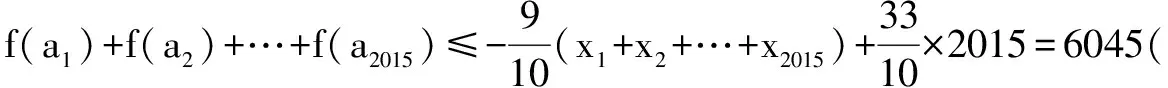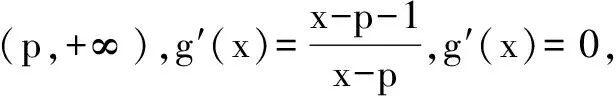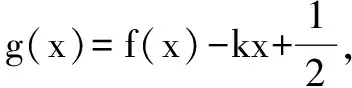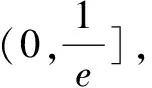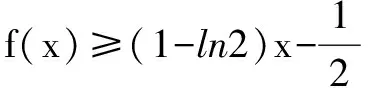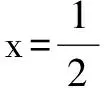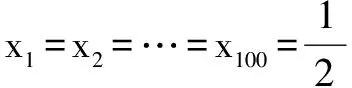解压轴题：轮换对称 化曲为直

许银伙 杨苍洲

(1.福建省泉州外国语中学 362000；2.福建省泉州第五中学 362000)

压轴题中有一类是条件不等式问题，其条件与结论都是关于某几个变量的轮换对称式，而且这几个变量的和为定量，结论是这几个变量的某个函数值和的形式.针对这类问题，本篇介绍的解决方法是：构造函数，求出函数图象在变量均值处切线方程，证明函数图象在指定范围内恒在切线上方或下方，把所求函数值的和放缩为切线函数值的和，从而解决问题.

例题1 (2009年金考卷猜题卷(一))设函数f(x)=-x3-2mx2-m2x+1-m(其中m>-2)的图象在x=2处的切线与直线y=12-5x平行.

(1)求m的值和该切线的方程；

(2)若对∀x1,x2∈[0,1]，|f(x1)-f(x2)|≤M恒成立，求M的最小值；

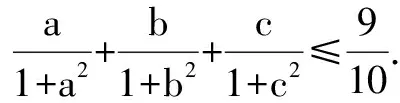
分析与解(1)切线的方程为： 5x+y-10=0.

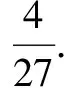
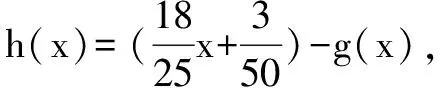
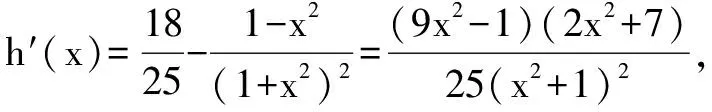
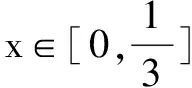
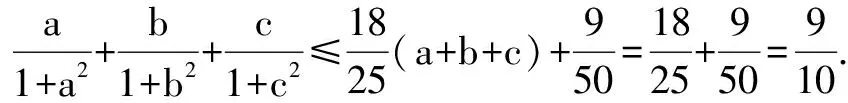
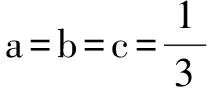
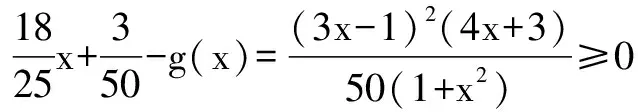
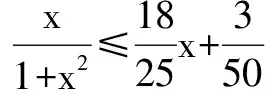
方法三(配套参考解答)

f(x)=(1+x2)(2-x)，由(Ⅱ)得：当x∈[0,1]时，

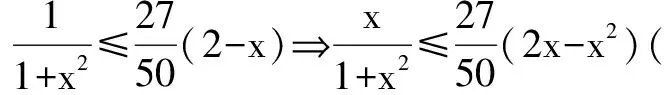
由已知得

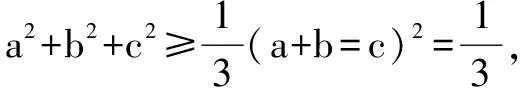
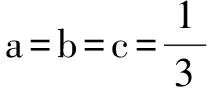
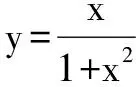
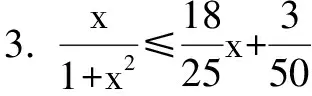
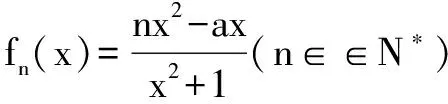
(1)求a的值及f1(x)的单调区间；

(2)是否存在实数k，使得射线y=kx(x≥-3)与曲线y=f1(x)有三个公共点？若存在，求出k的取值范围；若不存在，说明理由；

(3)设x1,x2,…,xn为正实数，且x1+x2+…+xn=1，证明：

fn(x1)+fn(x2)+fn(x3)+…+fn(xn)≥0.

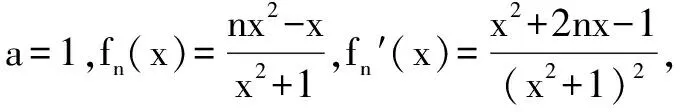
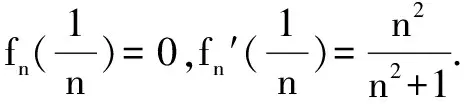
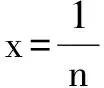
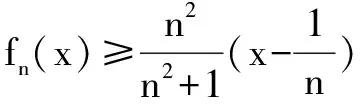
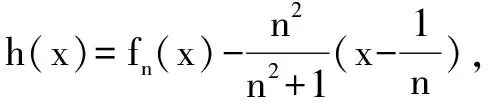
∵n∈N*且x∈(0,1)时，2n2+1-nx-nx3-x2=n(2n-x-x3)+(1-x2)>0，

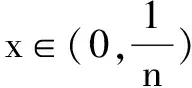
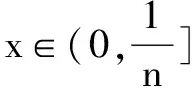
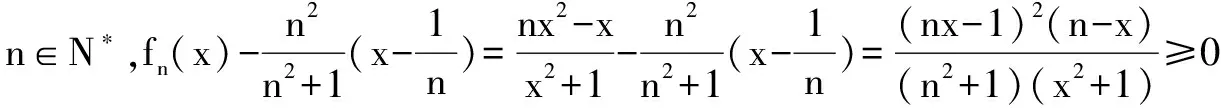
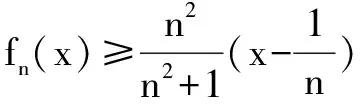
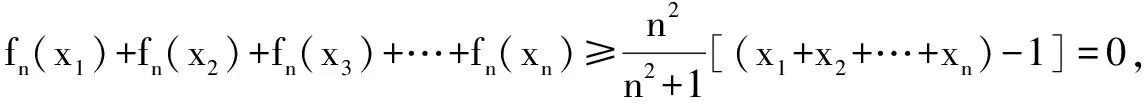
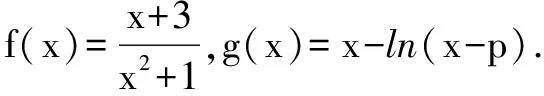
(2)判断函数g(x)的零点个数，并说明理由；

(3)已知数列{an}满足：0

若不等式f(a1)+f(a2)+…+f(a2015)≤g(x)在x∈(p,+∞)时恒成立，求实数p的最小值.

(2)g(x)零点个数：当p<-1时，有2个；当p=-1时，有1个；当p>-1时，没有. 理由略.

当x∈(p,p+1)时，g′(x)<0；当x∈(p+1,+∞)时，g′(x)>0.

∴g(x)在区间(p,p+1]单调递减，在区间(p+1,+∞)单调递增，g(x)min=g(p+1)=p+1，则p≥6044.

∴所求实数p的最小值为6044.

例题4 已知函数f(x)=xlnx.

(1)讨论f(x)的单调性；

(3)已知x1,x2,…,x100∈(0,1)，且x1+x2+…+x100=50，求f(x1)+f(x2)+…+f(x100)的最小值.

(2)当k>1-ln2时，g(x)有2个零点；

当k=1-ln2时，g(x)有1个零点；

当k<1-ln2时，g(x)没有零点.理由略.

则f(x1)+f(x2)+…+f(x100)≥(1-ln2)(x1+x2+…+x100)-50=-50ln2，

则所求f(x1)+f(x2)+…+f(x100)最小值为-50ln2.