对高中数学几种解题思想方法的探析

谢文法

(福建省泉州市安溪梧桐中学 362402)

高中数学各种题型较为复杂，解题问题过程中数学教师要引导学生运用数学思想方法来解答问题，比如分类讨论思想、换元思想、转化思想、化归思想、数形结合思想等，这样都能够帮助学生简化解题步骤，拥有较为清晰的解题思路，提高解题效率与正确率，减轻学生的数学解题压力.

一、运用分类讨论思想来实现科学分类

在高中数学解题过程中经常会用到分类讨论的数学思想方法，但是高中学生往往在运用分类讨论思想过程中出现问题，这都是由于学生在解题中分类不完整、讨论有遗漏或者重复的情况发生，导致最终的解题结果不规范、不完整，所以高中数学教师要善于引导学生科学运用分类讨论思想方法来帮助学生提高解题的效率与正确率.在题解过程中教师需要对题目中的条件合理、科学地展开分类，例如，求得函数y=|x+1|+|x-2|-2的值域，针对这个数学问题，学生就需要对x>2、-1≤x≤2、x<-1展开分类讨论，分完类之后通过分段函数中的图象得出最终函数的值域是[1，+∞).分类讨论一种较重要的数学解题思想，能够让高中学生通过题目中的条件去发现问题、分析问题、解决问题，此过程中能够培养高中学生数学思维的灵活性、缜密性、严谨性等.高中学生在运用分类讨论数学思想方法过程中要注重积累，寻找其中的共性与规律，对提高解题效率与正确率有着很大的帮助.

二、运用换元思想来解决难点问题

在解答高中数学问题过程中，学生经常因为缺乏已知条件而出现无从下手的情况，导致解题思维较为混乱，无法求得正确的解题结果，而在解题过程中运用换元思想，能够充分解决难点、重点数学问题，让复杂的数学问题简单化.换元法包含的内容比较多，其中包括化超越式为代数式、化分式为整式、化无理式为有理式、化高次为低次等内容.而换元的方法也有很多，其中包括三角换元、均值换元、局部换元等，这些方法都能够化未知为已知.但是在换元过程中通常需要注重分析自变量中的取值范围.比如，由复合函数g[f(x)]，求g(x)，这时候就可以运用换元法，令t=f(x)，最后把t转换为x，最终得到g(x)的解析式.

三、运用转化思想实现化抽象为直观

数学解题过程中的转化思想就是把问题由一种形式转化到另外一种形式中去，属于一项应用比较广泛的解题技巧，把复杂的高中数学问题简单化，帮助高中学生构建完整的数学知识体系，拥有较为清晰的解题思路.对于一些相对于较为复杂的数学题型，教师可以引导高中学生联系数学基本原理，寻求和数学题目中有关联的数学关系实施转化，最终求得解题结果.比如，在解决高中数学概率问题的时候就可以运用转化数学思想方法，例如：B、C、D三个人进行射击，每一个人射击一次，并且每一个人射中目标的概率是0.6，求最少有一个人击中目标的概率.对于这个问题，就需要展开三种情况来讨论，第一种是1个人击中另外2个人没有击中，第二种是2个人击中，1个人没有击中，第三种是3个人都击中了.这样的解题过程非常繁琐，很容易出现问题.针对这种情况教师就可以转化思考方向，从反面的角度去思考问题，也就是求得对立事件中3个人都没有击中，而只有1种情况，求得3个人中最少有1个人击中的概率是0.936.

四、运用化归思想实现化复杂为简单

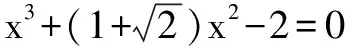
五、运用数形结合思想来实现以形助数

高中数学知识点较为抽象、复杂，很多数学问题如果仅仅是通过笔算的形式很难取得正确结果，高中学生的解题效率往往很低.高中教师可以引导学生运用数形结合思想，把数学问题运用图形的形式展现出来，实现以形助数的教学效果.

通过数学图形能够把难以理解、抽象的、无法表述的数学概念更为具体、形象化地展现出来，比如，把数学问题转变为代数问题，帮助高中学生看清楚数学问题的本质特征，让复杂的高中数学问题简单化.在历年的高考题中关于利用数形结合数学思想解题的题型非常多，所以高中数学教师就要加强对数形结合思想的重视，无论是在教学过程中还是在复习阶段都需要注重渗透数形结合数学思想，帮助高中学生更为透彻地理解所学知识.

总之，在高中数学解题过程中教师引导学生总结解题技巧与方法，必须拥有较为清晰的解题思路，才能够把数学解题思想方法运用到解题过程中，来提高解题效率与质量.