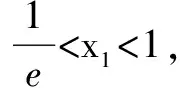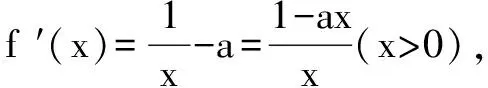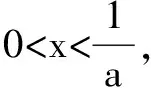函数零点和不等式的分类与证明

李秀元 夏志超

(湖北省武穴市实验高级中学 435400)

导数应用题中，有一类是研究函数的零点问题，往往涉及到证明函数两零点之和的一个不等式.通过试题分析，我们发现，有的不等式带有参数，有的不带参数，带有参数的不等式，一般反映的是函数零点与极值点的关系，即极值点的偏移问题.不带参数的不等式，由于含参函数的极值点可能为常数，因此也是极值点偏移，如果不等式中的常数与函数的极值点无关，我们称之为伪极值点偏移问题.下面通过例题，试图解读这些不等式的分类和证明方法，希望对同学们有所帮助.

类型一：极值点偏移问题

例1 已知函数f(x)=ex-ax(a∈R，e为自然对数的底数).

(1)讨论函数f(x)的单调性；

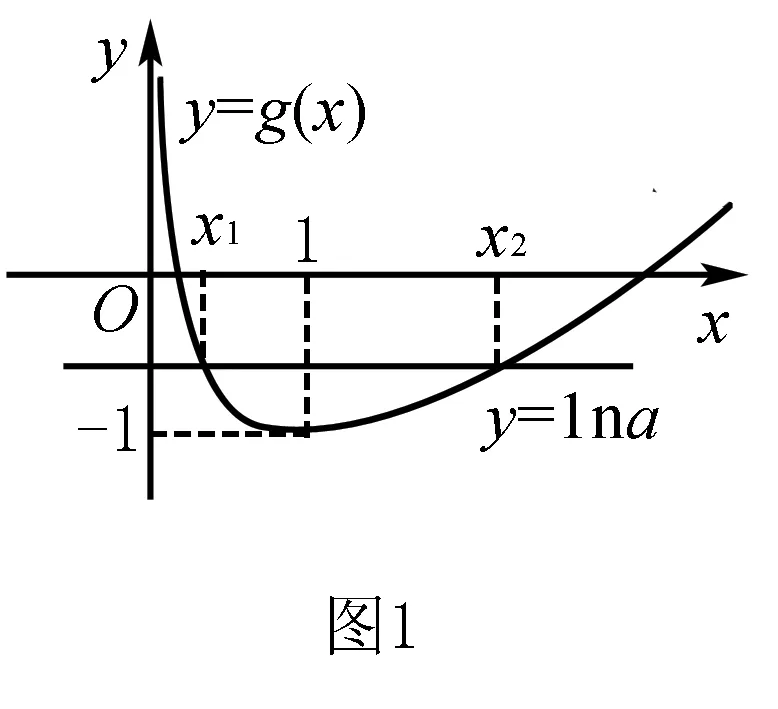
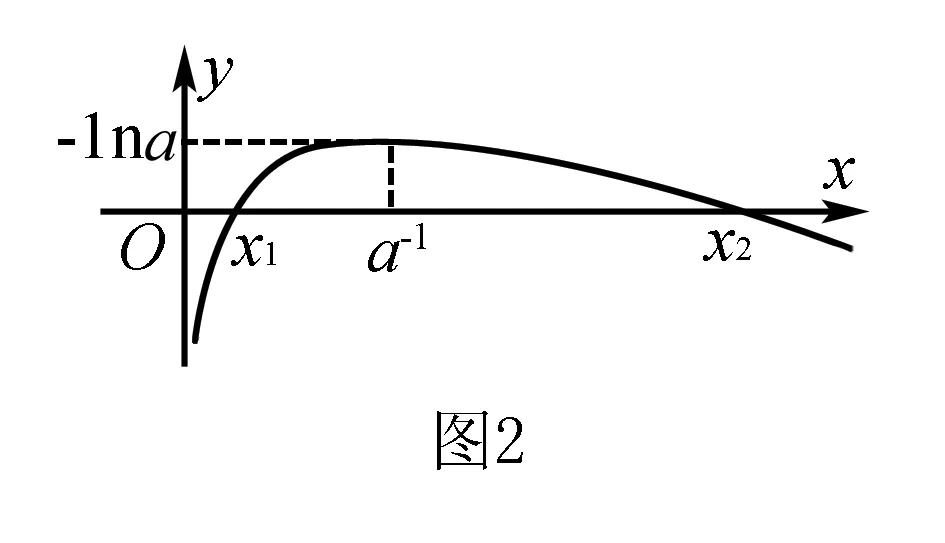
(2)若函数f(x)有两个零点x1，x2，且x1

①求实数a的取值范围；②求证：x1+x2<2lna.

分析依据对函数单调性的讨论，得到函数的极值点为x=lna，因此所证不等式与极值点相关，揭示的是函数极值点偏移.

解(1)当a≤0时，f(x)为R上的增函数；

当a>0时，f(x)为(-∞，lna)内的减函数，(lna，+∞)内的增函数.

(2)①实数a的取值范围是a>e(解题过程略)；

②依据讨论可知，x1

要证x1+x2<2lna，即证x1<2lna-x2.因为x1<2lna-x2f(2lna-x2)，又f(x1)=f(x2)=0，故只需证明f(x2)>f(2lna-x2)对x2>lna成立.

∴g(x)在(lna，+∞)内单调递增.

∴g(x)>g(lna)=0，即f(x)>f(2lna-x)，命题得证.

例2 (2016年全国卷Ⅰ)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1,x2是函数的两个零点，证明：x1+x2<2.

分析求参数a的取值范围，根据零点与方程根的关系，一般采取分离参变量，但在分离过程中，需要讨论x的取值，而且，参变分离之后的新函数式更复杂，在作图时需要界定图形的位置.因此考虑直接对原函数求导，得到函数的极值点为x=1，所以，所证不等式依然反映的是极值点的偏移问题.

解(1)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).

①若a=0，f(x)=(x-2)ex只有一个零点x=2.

③若a<0，当x≤1时，f(x)<0，函数f(x)在(-∞，1]内无零点.下面只需考虑函数f(x)在(1，+∞)内的零点个数.

由f′(x)=0得x=1或x=ln(-2a).

综上，a的取值范围为(0，+∞).

(2)不妨设x1f(2-x2)，即f(2-x2)<0.由于f(2-x2)=-x2e2-x2+a(x2-1)2，而f(x2)=(x2-2)ex2+a(x2-1)2=0，所以

f(2-x2)=-x2e2-x2-(x2-2)ex2.

设g(x)=-xe2-x-(x-2)ex，即证当x>1时，g(x)<0.

∵g′(x)=(x-1)(e2-x-ex),

∴当x>1时，g′(x)<0，g(x)为(1，+∞)内的减函数，而g(1)=0，所以当x>1时，g(x)<0，命题得证.

评析同样是极值点偏移问题，由于两者的极值点不一致，前者与参数有关，后者是常数，因此两题的处理方式似乎不一样.例1通过构造函数g(x)=f(x)-f(2lna-x)，证明g(x)>0对x>lna恒成立，这是极值点偏移问题的通常做法.例2则充分利用了零点的含义，只需证明不含参数的f(2-x2)<0，看似巧妙消参，本质上还是证明f(x)-f(2-x)>0.

类型二：伪极值点偏移

例3 已知a为实数，函数f(x)=ex-2-ax.

(1)讨论函数f(x)的单调性；

(2)若函数f(x)有两个零点x1，x2(x1

①求实数a的取值范围；②证明：x1+x2>2.

∴g(x)为(0,1)内的减函数，(1,+∞)内的增函数.而lna>-1，所以0

要证x1+x2>2，只需证x2>2-x1>1.

因为g(x)为(1,+∞)内的增函数，所以只需要证g(x2)>g(2-x1)，又g(x1)=g(x2)，所以只需证g(x1)>g(2-x1)，即g(x1)-g(2-x1)>0(x1∈(0,1)).

令h(x)=g(x)-g(2-x)(0

∴h(x)为(0，1)内的减函数.

∴h(x)>h(1)=0，从而g(x1)-g(2-x1)>0，命题得证.

评析所谓伪极值点偏移，实质上是借助零点与方程的关系，将原函数对应的方程分离参数之后，形成新函数的极值点偏移，参变分离后，新函数的极值点便与参数无关.

类型三：极值点偏移与不等式放缩

例4 已知a为实常数，函数f(x)=lnx-ax+1.

(1)讨论函数f(x)的单调性；

(2)若函数f(x)有两个不同的零点x1,x2(x1

当a≤0时，f′(x)>0，f(x)为(0，+∞)内的增函数；

在对例3的分析中，我们尝试过将极值点偏移与不等式的放缩相结合，结果不成功.虽然不等式的化简与证明中，不含参数要比含参数简单，但是什么情况下能把两者结合，是值得思考的，如例1中由于a>e，想通过证明x1+x2<2来实现x1+x2<2lna就是一个错误的决策，因为比一个大于2的数小的数不一定就比2小.实际上x1+x2>2，这样我们就在极值点偏移的基础上，得到函数零点和不等式的一个加强：2