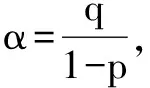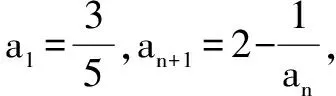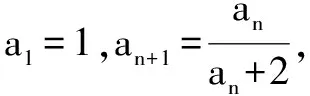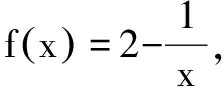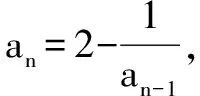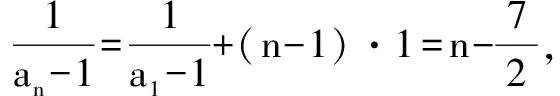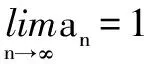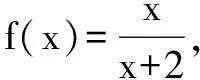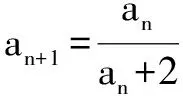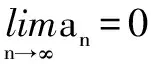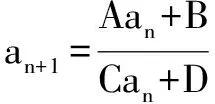迭代与迭代函数
2019-02-26张胜黎
张胜黎
(浙江省杭州市艮山中学 310003)
一、迭代函数的定义
迭代函数是重复的与自身复合的函数,这个过程叫做迭代,每一次对过程的重复称为一次“迭代”,而每一次迭代得到的结果将作为下一次迭代的初始值.
对于函数f(x),令f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),其中n≥2,n∈N*,我们将fn(x)称为函数f(x)的n次迭代.
迭代函数在高中数学中出现的频率很高,难度较大,本文将这类问题收集整理,以飨读者.
二、函数的二次迭代
例1 已知函数f(x)=asinx+bcosx(a,b∈Z),且满足{x|f(x)=0}={x|f(f(x))=0},则a的最大值为( ).
A.2 B.3 C.4 D.5
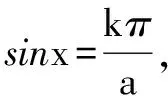
评注在这里,由f(0)=0得到b=0,简化了表达式.
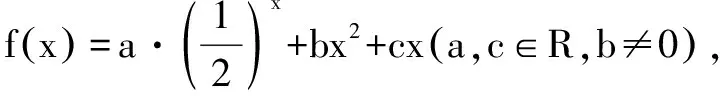
A.0 解由已知,f(0)=0,于是a=0,f(x)=bx2+cx. 当c=0时,{x|f(x)=0}={x|f(f(x))=0}={0},满足题意; 当c≠0时,f(f(x))=f(x)(bf(x)+c)=0等价于f(x)=0或bf(x)+c=0,只需方程bf(x)+c=b2x2+bcx+c=0无解,即Δ=b2c2-4b2c<0,因为b≠0,于是0 综上所述,0≤c<4.选C. 例3 巳知函数f(x)=ax2+bx+c(a>0,b,c∈R).设集合A={x|f(x)=x},B={x|f(f(x))=f(x)},C={x|f(f(x))=0}. (1)当a=2,A={2}时,求集合B; 解(1)由a=2,A={2},得方程f(x)=x有且只有一根2,即f(x)-x=2(x-2)2,于是b=-7,c=8. 又方程f(f(x))=0等价于f(x)=x1或f(x)=x2. 由于x1≠x2,可知方程f(x)=x1与f(x)=x2不会有相同的实根,从而方程f(f(x))=0有4个不相等的实根, 即集合C中的元素有4个. 例4 已知f(x)是一次函数,令f1(x)=f(x),fn(x)=f(fn-1(x)),其中n≥2,n∈N*,若f2018(x)=22018x+3(22018-1),求f(x). 解令f(x)=ax+b(a≠0),则f2(x)=f(ax+b)=a2x+(a+1)b,f3(x)=f(a2x+(a+1)b)=a3x+(a2+a+1)b,一般地,fn(x)=anx+(an-1+…+a+1)b,比较系数可知,a=2,b=3,即f(x)=2x+3. 例5 已知f(x)=x2-2x+c,f1(x)=f(x),fn(x)=f(fn-1(x))(n≥2,n∈N*),若函数y=fn(x)-x不存在零点,则实数c的取值范围是( ). 于是f(f(x))>f(x)>x也成立,重复上述过程,可知fn(x)>x也成立.选C. 例6 (2012年北大保送生考试题)已知f(x)是二次函数,且a,f(a),f(f(a)),f(f(f(a)))构成正项等比数列,求证:f(a)=a. 证明设f(a)=qa(q>0),则f(f(a))=f(qa)=q2a,f(f(f(a)))=f(q2a)=q3a. ②-①得ma2(q2-1)+na(q-1)=a(q2-q), 即(q-1)[ma2(q+1)+na]=qa(q-1).…④ ③-②,约去q后得(q-1)[ma2(q+1)q+na]=qa(q-1).…⑤ 假设q≠1,那么由④、⑤约去q-1后相减得 ma2(q+1)(q-1)=0,得q+1=0,这与q>0矛盾. 综上,q=1,即f(a)=a. 变式:已知f(x)是二次函数,且a,f(a),f(f(a)),f(f(f(a)))构成等差数列,求证:f(a)=a. 证明设f(a)=a+d,则f(f(a))=f(a+d)=a+2d,f(f(f(a)))=f(a+2d)=a+3d. ②-①得d[m(2a+d)+n]=d,…④, ③-②,同理得d[m(2a+3d)+n]=d,…⑤ 假设d≠0,那么由④、⑤约去d后相减得 md=0,这与m≠0,d≠0矛盾. 综上,d=0,即f(a)=a. 推广1 已知f(x)是三次函数,且a,f(a),f(f(a)),f(f(f(a))),f(f(f(f(a))))成正项等比数列,则f(a)=a. 推广2 已知f(x)是一元n(n∈N*)次多项式函数,且a,f(a),f(f(a)),f(f(f(a))),…,f(f(f…(f(a))))(共n+1个f)构成正项等比数列,则f(a)=a. 评注通过迭代,可以发现有向一个单一点收缩和会聚的一个集合,会聚到的这个点叫做吸引不动点. 递推数列an+1=f(an),在本质上就是函数迭代问题.我们记方程f(x)=x的解x0为函数f(x)的不动点. 例7 已知数列{an}中a1=1,an+1=2an+3,求an. 解记f(x)=2x+3,则an+1=f(an). 解方程f(x)=x,得x0=-3为函数f(x)的不动点. 由an+1=2an+3,可得an+1+3=2(an+3),所以数列{an+3}为等比数列,首项为a1+3=4,公比为2,所以an+3=(a1+3)·2n-1,所以an=2n+1-3. 解方程f(x)=x,得x0=1为函数f(x)的不动点. 解方程f(x)=x,得x1=0,x2=-1为函数f(x)的不动点. 递推数列的收敛点就是函数的不动点,函数迭代的重复反馈过程的活动,它的目的常常是为了逼近所需的目标或结果,这是工程物理中经常见到的.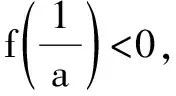
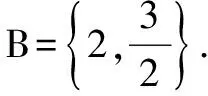
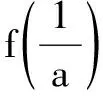
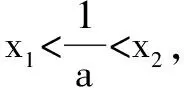
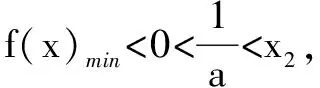
三、函数的n次迭代
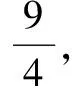
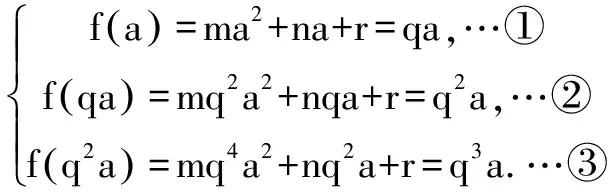
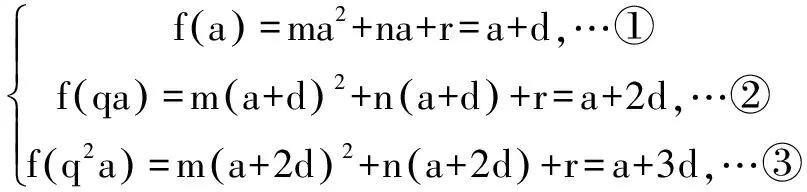
四、函数迭代在递推数列中的应用