浅谈用频率分布直方图估计总体的数字特征

■刘娟娟

在频率分布直方图中，运用样本的数字特征估计总体的数字特征，可以很好地考查同学们的识图能力，也可以很好地考查同学们的数学运算、数据分析和转化推理的核心素养，因此这类试题备受命题者的青睐。下面分别介绍如下，以供同学们参考。

一、利用频率分布直方图估计平均数

在频率分布直方图中，平均数的估计值等于每个小矩形的面积乘以小矩形底边中点的横坐标之和。

例1某校有高三文科学生1000人，统计这些学生高三上学期期中考试的数学成绩后，得到的频率分布直方图如图1所示。

图1

（1）求图中a的值，并估计本次考试成绩低于120分的人数。

（2）假设同组的每个数据可用该组区间的中点值代替，试估计本次考试成绩不低于120分的学生的平均分（结果保留一位小数）。

（1）利用频率之和为1，由图得到（a+0.015+0.0225+0.0175+0.015+0.01+a+0.005）×10=1，解得a=0.0075，所以本次考试成绩低于120分的学生共有1000—1000×10×（0.01+0.0075+0.005）=775（人）。

（2）由图1可知，不低于120分的频率为0.1，0.075，0.05，所以本次考试成绩不低于120分的学生的平均分为

在解答这类问题的过程中，需要弄明白的是频率分布直方图中小矩形的面积表示的是频率，平均数的计算公式为组中值乘以相应的频率作和。该题中需要注意的是当前的总体发生了变化，所以对应的频率已经不是对应的小矩形的面积了，应该重新核算。

跟踪练习1：对某校高三年级学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据这些数据作出了频数与频率的统计表（如表1）和频率分布直方图（如图2）。

表1

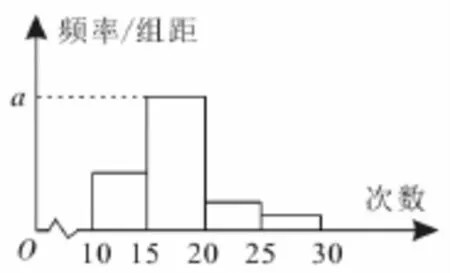
图2

（1）求表中M，p及图中a的值。

（2）若该校高三学生有240人，试估计这些学生参加社区服务的次数在区间［10，15）内的人数。

（3）试估计这些学生参加社区服务次数的平均数。

提示：（1）由题意知，解得M=40。因为频数之和为40，所以10+24+m+2=40，解得m=4，所以因为a是对应分组［15，20）的频率与组距的商，所以

（2）因为该校高三学生有240人，分组［10，15）内的频率是0.25，所以估计这些学生参加社区服务的次数在此区间内的人数为240×0.25=60。

（3）估计这些学生参加社区服务次数的平均数是12.5×0.25+17.5×0.6+22.5×0.1+27.5×0.05=17.25。

二、利用频率分布直方图估计众数

众数就是一组数据中出现次数最多的数据。在频率分布直方图中，用最高的小矩形底边中点的横坐标来估计众数。

例2某校对高二年级的男生进行体检，对他们的体重（单位：k g）数据进行整理后，分成六组，并绘制成频率分布直方图，如图3所示。

已知第三组［60，65）的人数为200。根据一般标准，高二年级的男生体重超过65k g属于偏胖，低于55k g属于偏瘦。

观察图中的信息，回答下列问题：

（1）用分层抽样的方法从偏胖的学生中抽取6人，对高二年级男生的日常生活习惯及体育锻炼情况进行调查，则各组应分别抽取多少人?

（2）根据频率分布直方图估计该校高二年级的男生体重的众数。

（1）设高二年级男生的总人数为n，由，可得n=1000。所以体重超过65k g的总人数为（0.03+0.02+0.01）×5×1000=300，由此可得抽样比为

在［65，70）这一组的人数为0.03×5×1000=150，应抽取的人数为；在［70，75）这一组的人数为0.02×5×1000=100，应抽取的人数为；在［75，80］这一组的人数为0.01×5×1000=50，应抽取的人数为所以在［65，70），［70，75），［75，80］这三组应抽取的人数分别为3，2，1。

（2）由图可知［55，60）这一组对应的小矩形最高，其底边中点的横坐标为57.5，由此可估计该校高二年级男生的体重的众数为57.5k g。

跟踪练习2：某中学举行电脑知识竞赛，将高一参赛学生的成绩进行整理后，分成五组，绘制成如图4所示的频率分布直方图。求高一参赛学生成绩的众数和平均成绩。

图4

提示：由图可知［60，70）这一组对应的小矩形最高，其底边中点的横坐标为65，所以高一参赛学生成绩的众数为65分。

由图可知从左到右的第一、二、三、四、五小组的频率分别为0.3，0.4，0.15，0.1，0.05，所以高一参赛学生的平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67（分）。

三、利用频率分布直方图估计中位数

在频率分布直方图中，中位数左边和右边的直方图的面积应该相等，由此可知，把频率分布直方图划分为左右两个面积相等的垂直于x轴的直线与x轴交点的横坐标可以用来估计中位数的值。

例3为了调查某厂工人生产某种产品的能力，随机抽查了20名工人某天生产该产品的数量，并绘制成如图5所示的频率分布直方图。

图5

（1）求这20名工人中一天生产该产品的数量在［55，75）的人数。

（2）求这20名工人一天生产该产品数量的中位数。

（1）由图可知（0.04×10+0.025×10）×20=13，所以这20名工人中一天生产该产品的数量在［55，75）的人数为13。

（2）由图知0.2+0.4＞0.5，所以中位数应位于第二个小矩形内。设中位数为x，则0.2+（x—55）×0.04=0.5，解得x=62.5，所以这20名工人一天生产该产品数量的中位数为62.5个。

第（1）问根据第i组的频数=第i组的频率×样本容量来计算。第（2）问根据中位数左边的直方图的面积为0.5，列方程求得中位数。

跟踪练习3：某校从高三抽出50名学生参加数学竞赛，由成绩得到如图6所示的频率分布直方图。由于一些数据丢失，试利用频率分布直方图求出这50名学生成绩的众数与中位数。

图6

提示：由众数的概念可知，众数是一组数据中出现次数最多的数。在频率分布直方图中，最高的小矩形的底边中点的横坐标即为众数，所以这50名学生成绩的众数应为75分。

由于中位数是所有数据中的中间值，故在频率分布直方图中体现的是中位数左右两边的小矩形的面积相等。因此在图6中，将所有小矩形的面积一分为二的垂直于x轴的直线与x轴交点的横坐标所对应的成绩即为中位数。因为0.004×10+0.006×10+0.02×10=0.04+0.06+0.2=0.3，所以前三个小矩形的面积的和为0.3，而第四个小矩形的面积为0.03×10=0.3，0.3+0.3＞0.5，所以中位数应位于第四个小矩形内。设第四个小矩形的底边长为x，因为高为0.03，所以有0.03x=0.2，解得x≈6.7。故这50名学生成绩的中位数应约为70+6.7=76.7（分）。