把我特征聚焦“三救”
2019-02-26周乐一
■周乐一
平均数、中位数、众数是用样本估计总体的重要数字特征,它们从不同的侧面对样本和总体进行了描述,从而可帮助我们更全面地把握事物的态势,为正确决策提供定性的支持。现分别介绍如下,希望对同学们掌握这“三数”能有所帮助。
一、对“三数”的理解
1.“三数”的概念。
(1)平均数:一组数据的总和除以数据的个数所得的商就是平均数。
(2)中位数:如果将一组数据按从小到大的顺序依次排列,当数据有奇数个时,处在最中间的一个数就是这组数据的中位数;当数据有偶数个时,处在最中间的两个数的平均数是这组数据的中位数。
(3)众数:在一组数据中,出现次数最多的数就是这组数据的众数。若有两个或多个数据出现的次数最多,且出现的次数一样,则这些数据都是这组数据的众数。若一组数据中,每个数据出现的次数一样多,则认为这组数据没有众数。
2.在频率分布直方图中也可以找到“三数”的有关信息。平均数是频率分布直方图的“重心”,它等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和;在频率分布直方图中,中位数左右两侧的直方图的面积应该相等,因而可以估计中位数的值;众数是频率分布直方图中最高的小矩形的底边的中点。利用频率分布直方图求出的平均数、中位数、众数均为近似值,往往与实际得出的数据不一致,但能粗略地估计平均数、中位数和众数。
3.实际问题中求得的平均数、中位数、众数都应带上单位。
二、“三数”特征的比较
平均数、中位数、众数都是描述数据集中趋势的特征数,它们都有各自的特征。
1.由于平均数与每一个样本数据都有关,所以任何一个样本数据的改变都会引起平均数的改变,这是中位数、众数都不具有的性质。正因如此,与中位数、众数比较起来,平均数可以反映出更多的关于样本数据总体的信息,因而其应用最为广泛,特别是在进行统计推理时有着重要的作用。但它的计算比较烦琐,并且容易受到极端数据的影响。
2.中位数是样本数据所占频率的等分线,它不受少数极端值的影响。但用中位数作为一组数据的代表,可靠性比较差,它对极端值的不敏感有时会成为缺点,因为这些极端值有时是不能忽视的。
3.众数体现了样本数据的最大集中点,它不受极端数据的影响,其求法也比较简便。当一组数据中个别数据变动较大时,适宜选择众数表示这组数据的集中趋势。但用众数作为一组数据的代表,可靠性也比较差,由于它对其他数据信息的忽视,使得其无法客观地反映总体特征。
三、“三数”的应用问题
1.求“三数”。
例1某次体检,6位同学的身高(单位:m)分别为1.72,1.78,1.75,1.8,1.69,1.77,则这组数据的中位数是____m。
将这6位同学的身高(单位:m)按照从低到高排列为1.69,1.72,1.75,1.77,1.78,1.8,这6个数的中位数是1.75与1.77的平均数,即为1.76,故这组数据的中位数是1.76m。
本题主要考查中位数的概念,是一道基础题。从历年的高考题目来看,涉及统计的题目往往不难,主要考查考生的识图、用图能力,以及应用数学知识解决实际问题的能力。
跟踪练习1:某样本中共有5个个体,其值分别为a,0,1,2,3。若样本的众数为1,则样本的中位数为( )。
A.0 B.1
C.2 D.3
提示:因为样本的众数为1,所以a=1,所以样本的中位数为1。故选B。
2.利用“三数”进行估计。
例2某工厂人员及他们的周工资(单位:元)构成如表1所示。
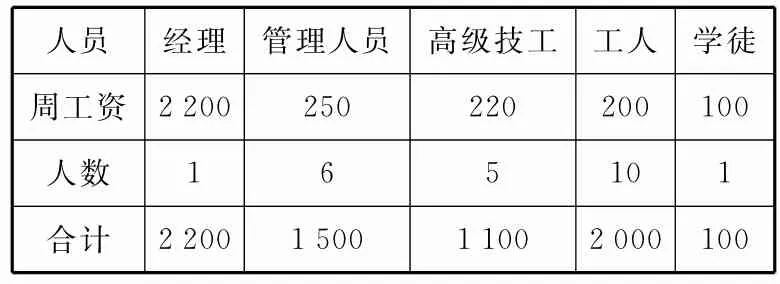
表1
(1)求该工厂人员周工资的众数、中位数、平均数。
(2)这个问题中,平均数能客观地反映该工厂人员的工资水平吗?为什么?
(1)由表1可知,该工厂人员周工资的众数为200元,中位数为220元,平均数为(2200+1500+1100+2000+100)÷23=300(元)。
(2)虽然该工厂人员周工资的平均数为300元,但由表1中所列出的数据可知,只有经理的周工资在平均数以上,其余人员的周工资都在平均数以下,故用平均数不能客观地反映该工厂人员的工资水平。
平均数受数据中极端值的影响较大,妨碍了对总体估计的可靠性,这时平均数反而不如众数、中位数更客观。
跟踪练习2:某校两组学生知识竞赛的成绩统计如表2所示。
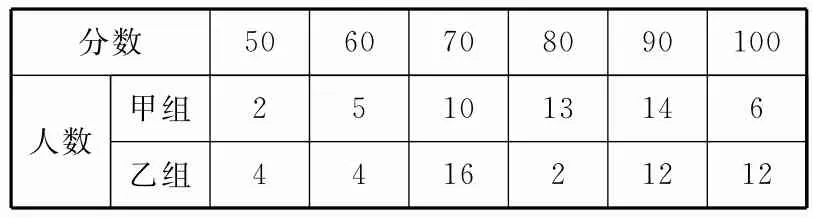
表2
已经算得两组的平均分都是80分,请根据你所学过的统计知识,试从成绩的众数、中位数及平均分以上(包括平均分)的人数等不同角度比较甲、乙两组的成绩。
提示:甲组成绩的众数是90分,乙组成绩的众数是70分;甲组成绩的中位数和乙组成绩的中位数都是80分;甲组平均分以上(包括平均分)的人数是33人,乙组平均分以上(包括平均分)的人数是26人。显然,甲组成绩好于乙组成绩。
3.利用频率分布直方图估计“三数”。
例3一学校举行某次月考后,从所有考生中随机抽取50名,对他们的数学成绩进行统计,得到的频率分布直方图如图1所示,则这次考试成绩的中位数的估计值是( )。
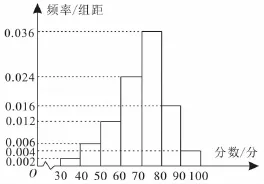
图1

由图1和选项可知,中位数应介于70~80之间,设中位数为70+x,依题意得10×(0.002+0.006+0.012+0.024)+0.036x=0.5,解得所以中位数的估计值为分。故选B。
频率分布直方图是重要的统计图,它从各个小组数据在样本容量中所占比例大小的角度来表示数据分布规律,能够很好地反映数据的变化趋势。利用频率分布直方图,既能计算样本中的频率、频数等有关数据,也可以求众数、中位数、平均数等数字特征的估计值。本题是通过读懂频率分布直方图,设出中位数并列方程进行求解的。
跟踪练习3:我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图2所示的频率分布直方图。
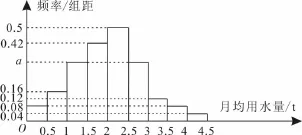
图2
(1)求图中a的值。
(2)估计该市居民月均用水量的中位数。
提示:(1)由频率分布直方图可知,月均用水量在[0,0.5]的频率为0.08×0.5=0.04。同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]几组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02。由1—(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.3。
(2)设中位数为x。因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x≤2.5。由0.5×(x—2)=0.5—0.48,解得x=2.04。所以估计该市居民月均用水量的中位数为2.04 t。
4.分类寻找数据。
例4一组数据共有7个数,记得其中有10,2,5,2,4,2,还有一个数没有记清,但知道这组数的平均数与众数的和是中位数的2倍,则这个数的所有可能值的和为( )。
A.9
B.3
C.6
D.7
设没有记清的这个数为x。由题意知众数是2,平均数是
若x≤2,则中位数为2,此时2×2=2+,解得x=—11;
若2<x<4,则中位数为x,此时2x=,解得x=3;
若x≥4,则中位数为4,此时4×2=2+,解得x=17。
综上可知,没有记清的这个数的所有可能值的和为—11+3+17=9。故选A。
本题在分类讨论的基础上,利用平均数、中位数和众数的关系,去找寻没有记清的数据,既考查了对样本数字特征的进一步理解,又考查了分析问题和解决问题的能力。
跟踪练习4:样本x1,x2,…,xn的平均数为x,样本的平均数为y),若样本的平均数为,且n>m,则实数a的取值范围为____。
提示:由题意知
又因为n>m,所以
故实数a的取值范围为
