直击高考,统计在线
2019-02-26韩文美
■韩文美
统计内容涉及统计的基本概念、抽样方法、总体分布、总体特征数及回归方程等,是每年高考的必考点。主要考点包括抽样方法的选择与计算,总体分布中的统计图表的识别与应用,总体特征数的计算与应用,回归方程的求解与应用,以及统计知识的交汇与综合应用问题等。
1.抽样方法的考查
主要考查抽样方法的概念和运算,以及运用统计知识解决实际问题的能力。主要以分层抽样为主。
例1(2018年全国卷Ⅲ文·14)某公司有大量客户,且不同年龄段的客户对其服务的评价有较大差异。为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样法、分层抽样法和系统抽样法,则最合适的抽样方法是____。
由于不同年龄段的客户对其服务的评价有较大差异,根据抽样方法的性质知最合适的抽样方法是分层抽样法。
简单随机抽样是系统抽样和分层抽样的基础,三种抽样方法都是等可能抽样,体现了它们的客观性和公平性。但各自又有各自的特点,在实际应用中要注意三种抽样方法的区别。
2.总体分布的考查
总体分布的考查主要通过统计图表的形式呈现,包括统计中常用的频率分布表、频率分布直方图、频率分布折线图、总体密度曲线、茎叶图、扇形图等。①图表的比较信息,确定不同数据的结果情况。②图表的数据信息与统计信息,通过识图表、读图表,从图表中获取数据信息并加以统计,从而通过这些统计图表给出相应的统计信息,或通过相应的统计信息得出统计图表。高考考查中主要以频率分布表、频率分布直方图等为主,经常出现在选择题、填空题中,难度不大。
例2(2018年全国卷Ⅰ文、理·3)某地区经过一年的新农村建设,农村的经济收入增加了1倍。为更好地了解该地区农村的经济收入变化情况,统计出该地区新农村建设前后农村的经济收入构成比例,如图1所示,则下面结论中不正确的是( )。

A.新农村建设后,种植收入减少了
B.新农村建设后,其他收入增加了1倍以上
C.新农村建设后,养殖收入增加了1倍
D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
假设建设前的经济收入为100,则建设后的经济收入为200。可得建设前的种植收入为100×60%=60,建设后的种植收入为200×37%=74,A项错误。建设前的其他收入为100×4%=4,建设后的其他收入为200×5%=10,B项正确。建设前的养殖收入为100×30%=30,建设后的养殖收入为200×30%=60,C项正确。建设后,养殖收入与第三产业收入所占比例之和为30%+28%=58%,超过了经济收入所占比例的一半,D项正确。故选A。
通过统计中扇形图的识别与应用、数据信息的处理来考查数据分析的数学核心素养。解决此类统计图表问题,关键是从统计图表中正确读出对应的数据信息,并加以正确转化,从而合理地进行数据分析与数据处理。
3.总体特征数的考查
总体特征数中,众数、中位数和平均数是三种最常用的特征数,为我们提供了关于样本数据的特征信息,从不同的侧面反映数据的分布状态。标准差、方差用来考查样本数据分散程度的大小,标准差、方差越大,数据的离散程度越大,标准差、方差越小,数据的离散程度越小。特别是在样本数据的平均数相同的情况下,经常通过考察标准差或方差来进一步分析数据的分散程度。
例3(2018年江苏卷·3)已知5位裁判给某运动员打出的分数的茎叶图如图2所示,那么这5位裁判打出的分数的平均数为____。
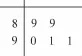
图2
由茎叶图中的数据知,这5位裁判打出的分数分别为89,89,90,91,91,它们的平均数为
本题巧妙地把茎叶图与平均数加以交汇进行考查。平均数和中位数能反映一组数据的集中趋势,而标准差和方差能反映一组数据的稳定程度。
4.回归方程的考查
变量之间的相关关系主要包括两个变量之间关系的确定,以及当两个变量具有线性相关关系时回归方程的求解及其应用等。解答相关问题时,要厘清两个变量之间的函数关系与相关关系的区别与联系,以及准确确定回归直线,根据回归直线的系数公式正确地求出回归方程,从而进一步加强数学应用意识,培养运用所学知识分析问题和解决问题的能力。
例4(2018年全国卷Ⅱ文、理·18)图3是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图。
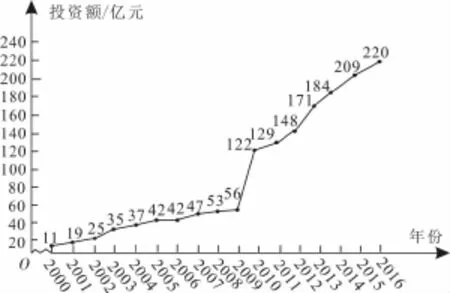
图3
为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型。根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型①:ˆy=—30.4+13.5t。根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②:ˆy=99+17.5t。
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值。
(2)你认为用哪个模型得到的预测值更可靠?并说明理由。
(1)利用模型①,得该地区2018年的环境基础设施投资额的预测值为ˆy=—30.4+13.5×19=226.1(亿元);利用模型②,得该地区2018年的环境基础设施投资额的预测值为ˆy=99+17.5×9=256.5(亿元)。
(2)利用模型②得到的预测值更可靠。理由如下:
从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=—30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述该地区环境基础设施投资额的变化趋势。2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型②,可以较好地描述2010年以后该地区的环境基础设施投资额的变化趋势。因此利用模型②得到的预测值更可靠。
从计算结果来看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值256.5亿元的增幅比较合理,说明利用模型②得到的预测值更可靠。
本题主要考查线性回归方程的特征及其应用,考查对统计数据的分析与处理能力。数据的数学化分析是数学对自然科学的一大重要贡献,如线性回归方程的预测与实际已有数据的比对,统计中线性回归模型必过数据中心点等,是判断模型预测可靠性的重要依据。
5.统计综合问题的考查
在统计中,往往会把抽样方法、总体分布、总体特征数、线性回归方程等几个相关的知识点加以综合进行考查。有时还会把相应的代数、几何、概率等知识加以交汇,综合考查统计知识的应用问题,这类试题是近几年高考中的热点试题之一,希望同学们能多加重视。
例5(2018年全国卷Ⅰ文·19)某家庭记录了未使用节水龙头50天的日用水量(单位:m3)和使用了节水龙头50天的日用水量,得到的频数分布表如表1、2所示。
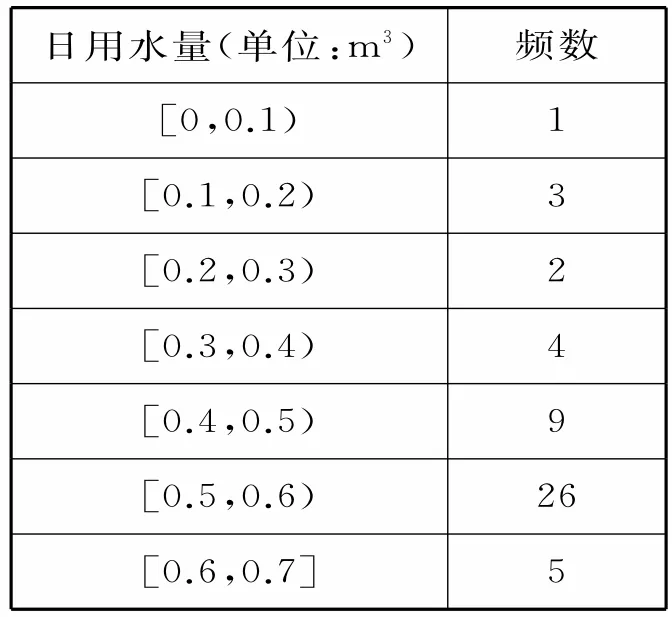
表1
(1)画出该家庭使用节水龙头50天的日用水量的频率分布直方图。
(2)估计该家庭使用节水龙头50天后,日用水量小于0.35m3的概率。
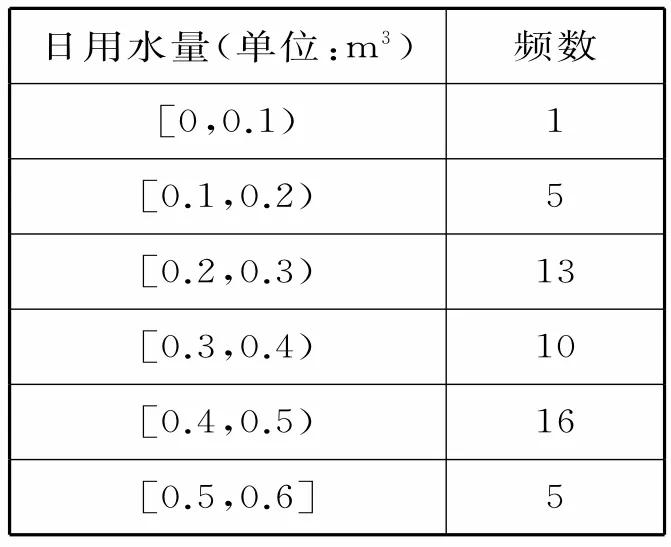
表2
(1)该家庭使用节水龙头50天的日用水量的频率分布直方图如图4所示。
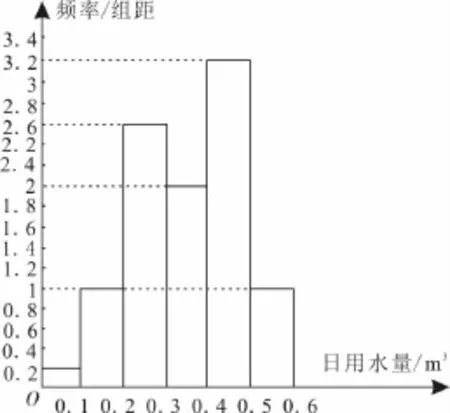
图4
(2)该家庭使用节水龙头50天后,日用水量小于0.35m3的频率为0.2×0.1+1×0.1+2.6×0.1+2×0.05=0.48,因此该家庭使用节水龙头50天后,日用水量小于0.35m3的概率的估计值为0.48。
本题巧妙地把统计中的数据处理、总体分布与总体特征数、频率与概率等概念加以综合,考查统计的数据处理能力、运算求解能力和应用意识等。
