湍流模型对瞬态流固耦合换热数值模拟影响分析

丁文杰，郭海兵，黄洪文，郭斯茂

(中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900)

聚变-裂变混合能源堆(Z-FFR)利用电磁内爆加热并压缩氘氚靶丸发生聚变，产生聚变中子驱动次临界包层实现能量放大。由于聚变中子源的脉冲特性，98.7%的能量在0.01 s 内沉积于次临界包层的燃料中[1]，燃料瞬时温度阶跃最大可达300 K[2]。Z-FFR的瞬态释能特性与传统稳态释能系统存在较大差异，给次临界包层的热工水力设计带来未知和不确定因素。已有部分学者对功率瞬态变化条件下的流动传热问题展开研究。1960年，Sparrow等[3]通过对湍流模型求解近似解获得了圆管湍流流动的瞬态换热响应结果。1967年，Soliman等[4]通过考虑湍流边界层的效应获得了平板温度变化的解析解，但该结果的换热系数高出实验值的50%。1983年，Steward等[5]开展了液氦在受到壁面阶跃热流量时瞬态强制对流换热响应的实验研究。2005年，Bhowmik等[6]对电加热片的瞬态对流换热进行了实验研究，并根据实验数据拟合了计算瞬态换热系数的经验关系式。Liu等[7-9]对氦气及氮气外掠加热平板、水平圆柱时功率指数上升的瞬态强制对流换热进行了理论与实验研究，并根据理论与实验研究的结果拟合了计算瞬态换热系数的经验关系式。

以上研究通过理论或实验的方法获得了瞬态对流传热过程中的响应，但这些文献均未给出不同湍流模型对数值模拟结果的影响。本文基于ANSYS Fluent程序和Liu等[7-9]的实验数据，对瞬态对流换热过程中的湍流模型进行敏感性分析。

1 数值模型

1.1 几何建模

热负载功率指数提升实验平台由日本神户大学Liu等搭建，用于分析高温气冷堆功率瞬变过程中的对流换热影响。该平台实验段为一水平放置、内径20 mm的圆形流道，流道内的流体可采用氦气或氮气，在流道中心位置水平放置加热元件，该加热元件为薄平板状或细圆柱状。以薄平板状加热元件为例(图1)，加热元件为一厚0.1 mm、宽4.0 mm、长50 mm的金属铂片，为防止实验过程中加热元件发生移动，金属铂片两端均采用长为45 mm的铜片固定。

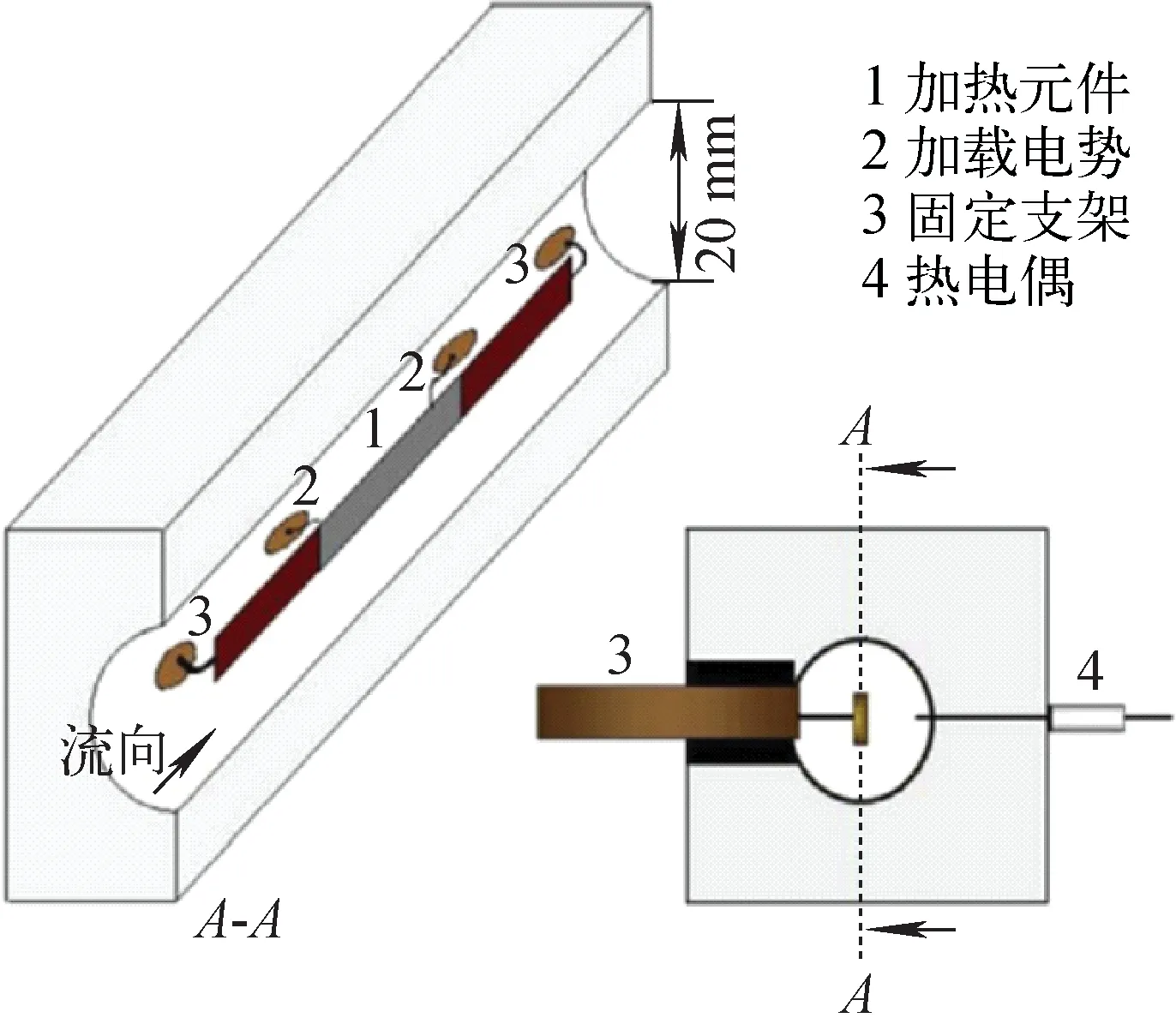
图1 实验段示意图Fig.1 Schematic of test section

根据上述描述，采用GAMBIT软件对该实验段进行建模。当加热元件为细圆柱状时，可直接根据轴对称原则建立二维模型。当加热元件为薄平板状时，固体过薄导致网格划分量大，不利于瞬态计算，为此，分别建立三维模型与简化二维模型计算相同的稳态工况，两种模型计算的壁面平均换热系数相对偏差为2.1%，即加热元件为薄平板状时同样可采用二维模型。薄平板状加热元件的几何模型如图2所示。

图2 薄平板状加热元件的几何模型Fig.2 Geometric model of thin plate heating element

1.2 物性参数选取

1) 流体热物性

实验段出口压力为0.5 MPa，且实验过程中保持不变，故流体热物性参数可看作是仅随温度变化的函数。通过文献[10-14]可获得氮气与氦气在0.5 MPa、300～1 000 K下的热物性参数，进而采用多项式拟合的方法可获得两种气体热物性参数的拟合关系式，供ANSYS Fluent程序分析使用。

氮气热物性拟合关系式如下：

ρN2=-1.479 8e-8T3+3.766 56e-5T2-

0.034 01T+12.801 67

(1)

cp,N2=-3.535 35e-10T3+ 8.679 65e-7T2-

4.642 14e-4T+ 1.120 24

(2)

λN2=-7.857 14e-9T2+

6.724e-5T+6.577 38e-3

(3)

ηN2=-1.333 33e-5T2+

0.050 76T+4.063 1

(4)

式中：ρ为密度，kg/m3；cp为比定压热容，kJ·kg-1·K-1；λ为热导率，W·m-1·K-1；η为动力黏性系数，μPa·s；T为温度，K。

氦气的比定压热容取常数5.19 kJ·kg-1·K-1，其余热物性参数拟合关系式如下：

ρHe=-2.095 96e-9T3+5.343 07e-6T2-

0.004 83T+1.820 48

(5)

λHe=-7.202 38e-8T2+

3.842 3e-4T+0.048 09

(6)

ηHe=-8.333 33e-6T2+

0.048 19T+6.284 52

(7)

2) 固体热物性

在计算过程中，假定固体材料的热物性不随温度发生变化。根据文献[15]可获得金属铂与铜的热物性参数，如表1所列。

表1 固体材料物性参数Table 1 Property parameter of solid material

1.3 湍流模型与网格无关性分析

ANSYS Fluent程序提供了大量的湍流模型，如k-ε模型、k-ω模型等，其中每一大类的湍流模型又包含若干个子类模型。考虑到本文所研究的对象为简单的壁面流动，并不考虑强旋流动和弯曲壁面的影响，故选取4种典型的湍流模型进行分析，包括标准k-ε模型、标准k-ω模型、过渡SST模型以及LRRIP雷诺应力模型(RSM模型)。

壁面函数法是基于所计算问题的壁面附近黏性支层以外区域的无量纲速度与温度分别服从对数律分布的假设而获得的[16]。在功率指数瞬变过程中，靠近加热壁面附近的流体密度将随温度瞬变而改变，引起近壁处的流场发生变化，破坏了无量纲速度与温度的对数律分布假定。为此，通过控制边界层网格y+的大小，确保所有湍流模型的壁面模型均采用强化壁面处理而非壁面函数法。建立5套网格划分方案，采用不同湍流模型进行稳态模拟，结果示于图3，可见，当y+在1左右时，各湍流模型模拟的稳态换热系数几乎保持不变，即具有网格无关解。

图3 不同网格划分方案下的稳态换热系数Fig.3 Steady-state heat transfer coefficient in different grids

2 计算结果与分析

2.1 瞬态过程中的流固耦合换热特性

在功率指数增长实验过程中，加热元件被直流电源加热，采用控制系统对热功率进行控制并测量其两端的电压与电流，进而根据计算的电阻值反推加热元件的体平均温度。加热元件的体功率瞬态变化如下：

Q(t)=Q0exp(t/τ)

(8)

式中：t为瞬态时间；τ为指数增长周期；Q(t)为t时刻加热元件的体功率密度；Q0为初始时刻的体功率密度。

加热元件的等效表面热流密度采用下式计算：

(9)

式中：q(t)为t时刻加热元件的等效表面热流密度；δ为平板加热元件的厚度(当加热元件为圆柱状时为该圆柱的半径)；ρs、cs、Ts分别为加热元件的密度、比热容和体平均温度。

通过式(9)获得加热元件的等效表面热流密度，该等效热流密度的最大不确定度为2.4%[10]。

采用k-ε模型模拟氦气外掠平板流动的功率、温升瞬态变化，结果示于图4。其模拟工况为：流体速度10 m/s、气体入口温度313 K、功率指数增长周期分别为92 ms和735 ms。加热元件的温升与主流流体的温升分别代表加热元件温度、主流流体温度与气体入口温度的差值。从图4可看出，在加热元件的体功率指数增长过程中，其等效表面热流密度、体平均温度以及流体温度也随之呈指数形式增长。根据式(9)可计算出：当指数增长周期为92 ms时，加载到金属铂上的热量约有20%将会被冷却流体以对流的形式带走，而剩下的近80%的热量仍留在固体内，使固体域的温度升高；当指数增长周期为735 ms时，约有60%的热量被流体带走，而仅有约40%的热量留在固体内。不难发现，瞬态加热过程与稳态时热量全部传递到流体的过程存在明显的不同：在加热功率指数增长的过程中，加热功率一部分被流体以对流形式带走，而另一部分继续留在固体内，使固体升温。流体对流换热带走的热量占加热功率的比值与加热功率的提升速率有关，即提升速率越快，对流换热带走的热量占比越低。

当模拟工况中采用氦气工质，且流体速度为10 m/s、气体入口温度为313 K、功率指数增长周期为92 ms时，不同瞬态时刻沿金属铂中心位置法线方向的流体速度分布与温度分布示于图5(y为网格中心点距金属铂中线位置的距离)。从图5a可看出，流体速度沿法线方向的分布随时间而变化，这与采用定热物性假设而获得的速度分布不变有明显的差异。此外，随着时间的增加，靠近加热壁面流体的流速不断减小，而远离加热壁面流体的流速不断增加，这是由于壁面温度不断升高进而使靠近壁面的流体热膨胀，且流体黏性增大所导致的。从图5b可看出，在靠近加热壁面1 mm处的流体温度沿法向方向剧烈变化，而远离加热壁面的流体温度仍保持入口温度。

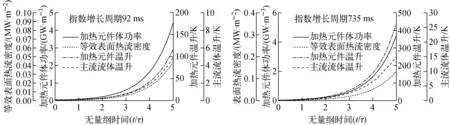
图4 不同指数增长周期下的传热特性Fig.4 Heat transfer characteristic in different periods

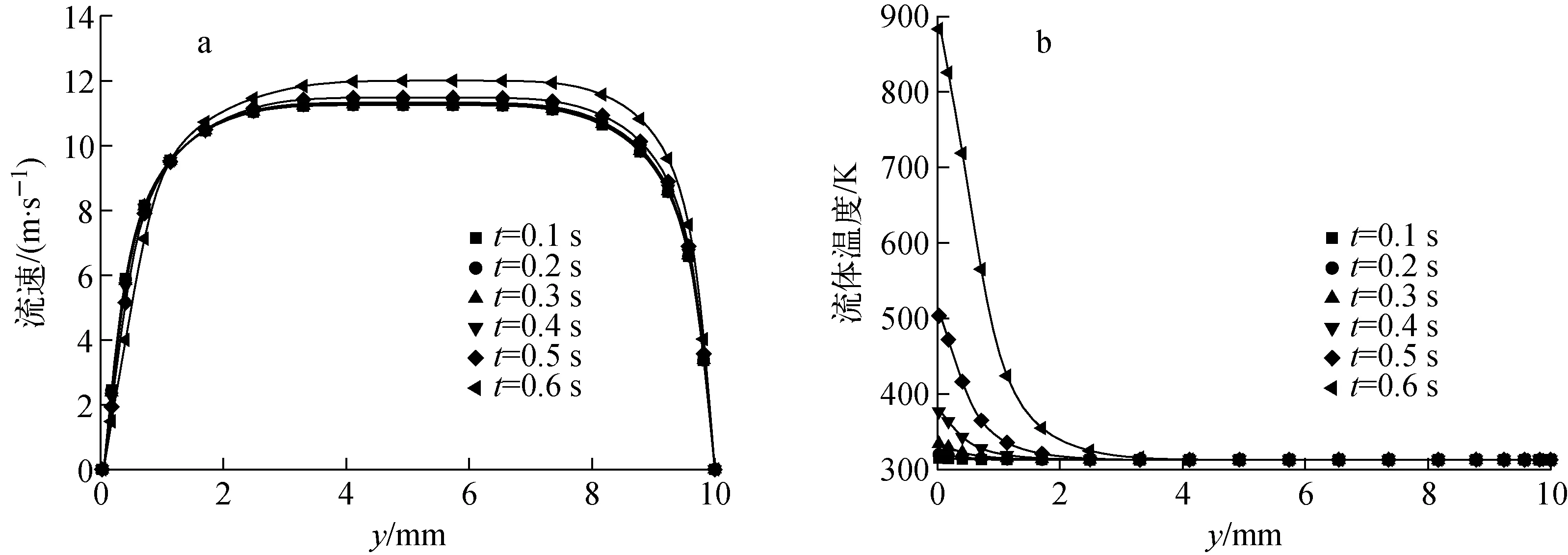
图5 不同时刻的流体速度与温度分布Fig.5 Velocity and temperature distribution at different time

2.2 湍流模型对瞬态流固耦合换热的影响

1) 氮气外掠平板流动实验

使用不同湍流模型对氮气外掠平板流动实验(实验工况为：流体速度4 m/s、气体入口温度313 K、功率指数增长周期174 ms)进行模拟，将模拟的固体域温度以及根据式(9)计算的等效表面热流密度与实验结果进行对比，以分析不同湍流模型对流固耦合换热的影响，结果示于图6。从图6a可看出，采用SST模型模拟的加热元件体温度略高于其他3种模型的模拟结果，且4种模型的模拟结果整体上均与实验数据相吻合。从图6b可看出，不同湍流模型模拟的等效表面热流密度变化趋势一致，但4种模型的模拟结果均低于实验值，其中k-ε模型与实验数据最接近，而SST模型与实验数据相差最大。

图6 氮气外掠平板流动的模拟结果与实验数据的对比Fig.6 Comparison between numerical results and experimental data for nitrogen gas flowing over plate

为整体考虑湍流模型的性能，需进一步比较各模型的均方根偏差E。定义E为：

(10)

式中：qCAL为根据数值模拟结果获得的等效表面热流密度；qEXP为根据实验数据获得的等效表面热流密度；n为实验数据点个数。

根据式(10)计算各模型的均方根偏差，结果示于图7。从图7可看出，SST模型的均方根偏差最大，接近28.3%。本次模拟结果中，均方根偏差最小的为k-ε模型，RSM模型次之，SST模型最大。

2) 氦气外掠平板实验

使用4种湍流模型对氦气外掠平板流动实验(实验工况为：流体速度10 m/s、气体入口温度313 K、功率指数增长周期92 ms)进行模拟，并与实验结果进行对比，结果示于图8。从图8可看出，4种湍流模型计算的等效表面热流密度均低于实验值，其中k-ε模型与RSM模型与实验值较为接近，而k-ω模型及SST模型与实验值偏差较大。

图7 各模型模拟氮气外掠平板流动的均方根偏差Fig.7 Root mean square deviation of different turbulence models for nitrogen gas flowing over plate

各模型的均方根偏差示于图9。从图9可看出，采用4种湍流模型获得的等效表面热流密度均与实验值有较大偏差，均方根偏差均超过20%。但相比于其他3种湍流模型，k-ε模型仍是均方根偏差最小的模型。

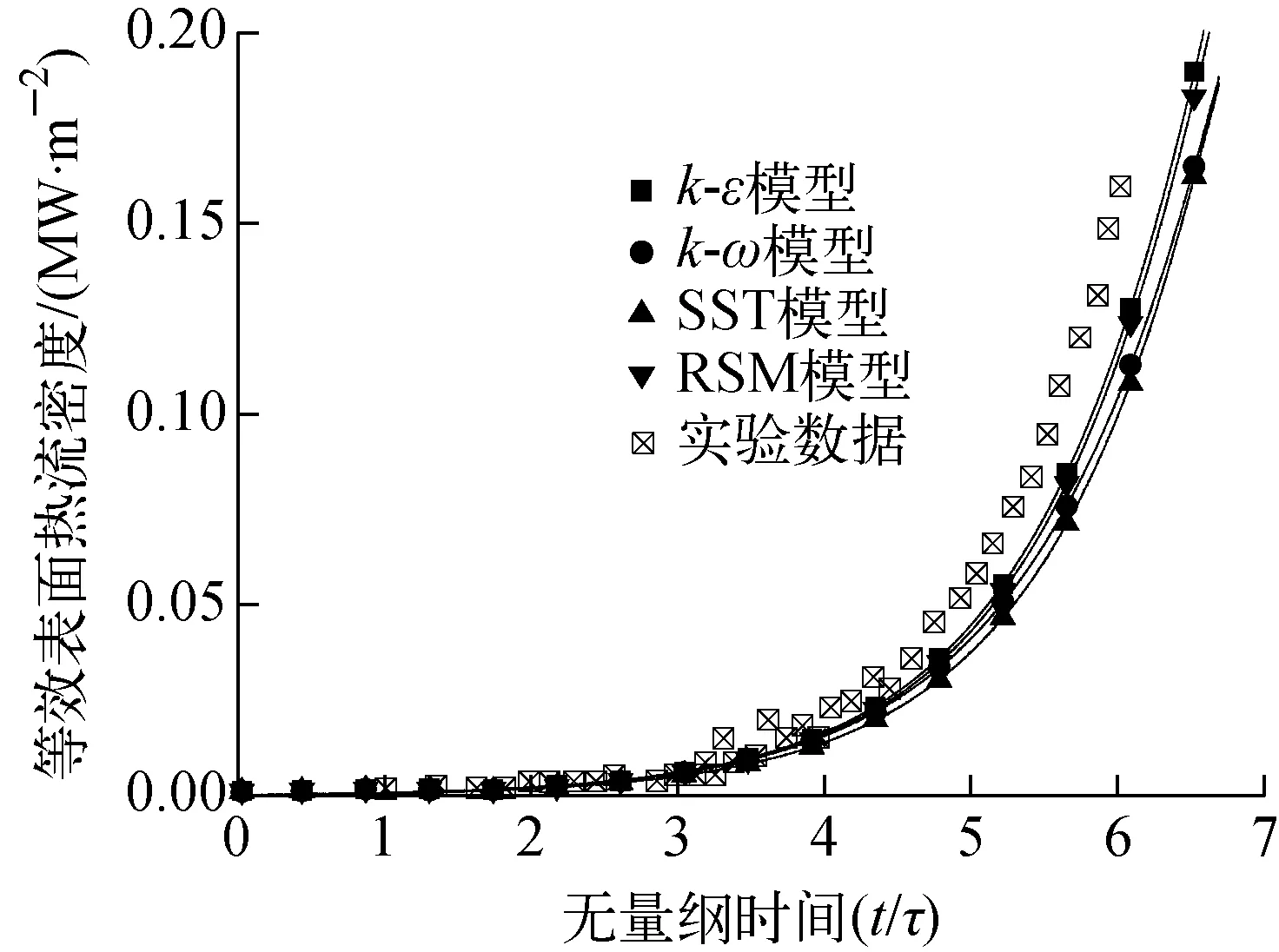
图8 氦气外掠平板流动的模拟结果与实验值的对比Fig.8 Comparison between numerical results and experimental data for helium gas flowing over plate

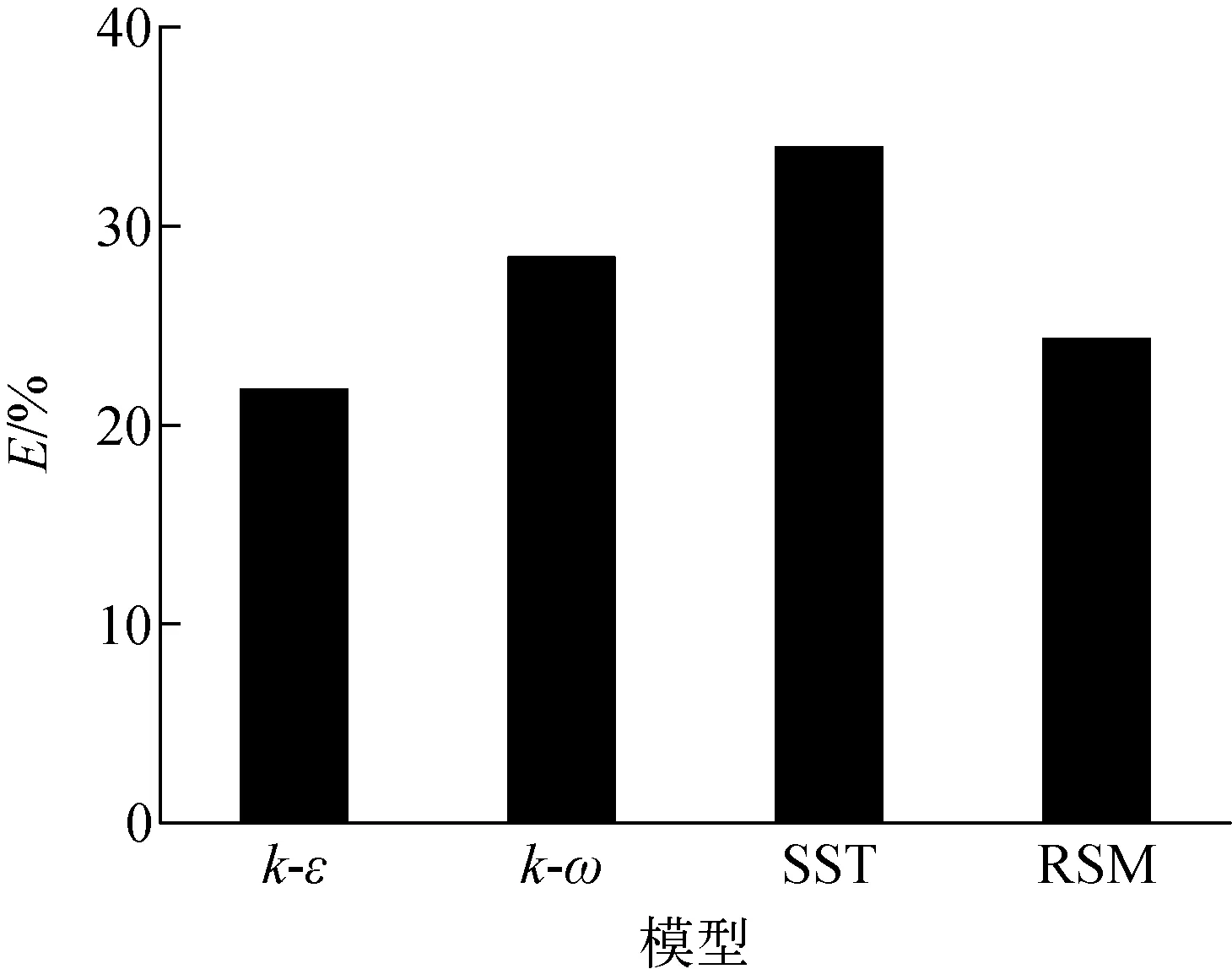
图9 各模型模拟氦气外掠平板流动的均方根偏差Fig.9 Root mean square deviation of different turbulence models for helium gas flowing over plate

3) 氦气外掠圆柱实验

使用4种湍流模型对氦气外掠圆柱流动实验(实验工况为：流体速度10 m/s、气体入口温度313 K、功率指数增长周期1.5 s)进行模拟，并与实验结果进行对比，结果示于图10。从图10可看出，4种湍流模型计算的等效表面热流密度相互间差异较小，且均与实验值相吻合。

各模型的均方根偏差示于图11。从图11可看出，采用4种湍流模型获得的等效表面热流密度与实验值的均方根偏差均低于16%。其中，k-ε模型与RSM模型的均方根偏差较小，SST模型次之，k-ω模型最大。

4) 数值模拟与实验值的对比分析

本研究选取的4种湍流模型，根据求解变量的差异又可分为ε类湍流模型与ω类湍流模型。其中，标准k-ε模型与RSM模型属于ε类湍流模型，而标准k-ω模型与过渡SST模型则属于ω类湍流模型。

图10 氦气外掠圆柱流动的模拟结果与实验数据对比Fig.10 Comparison between numerical results and experimental data for helium gas flowing over cylinder

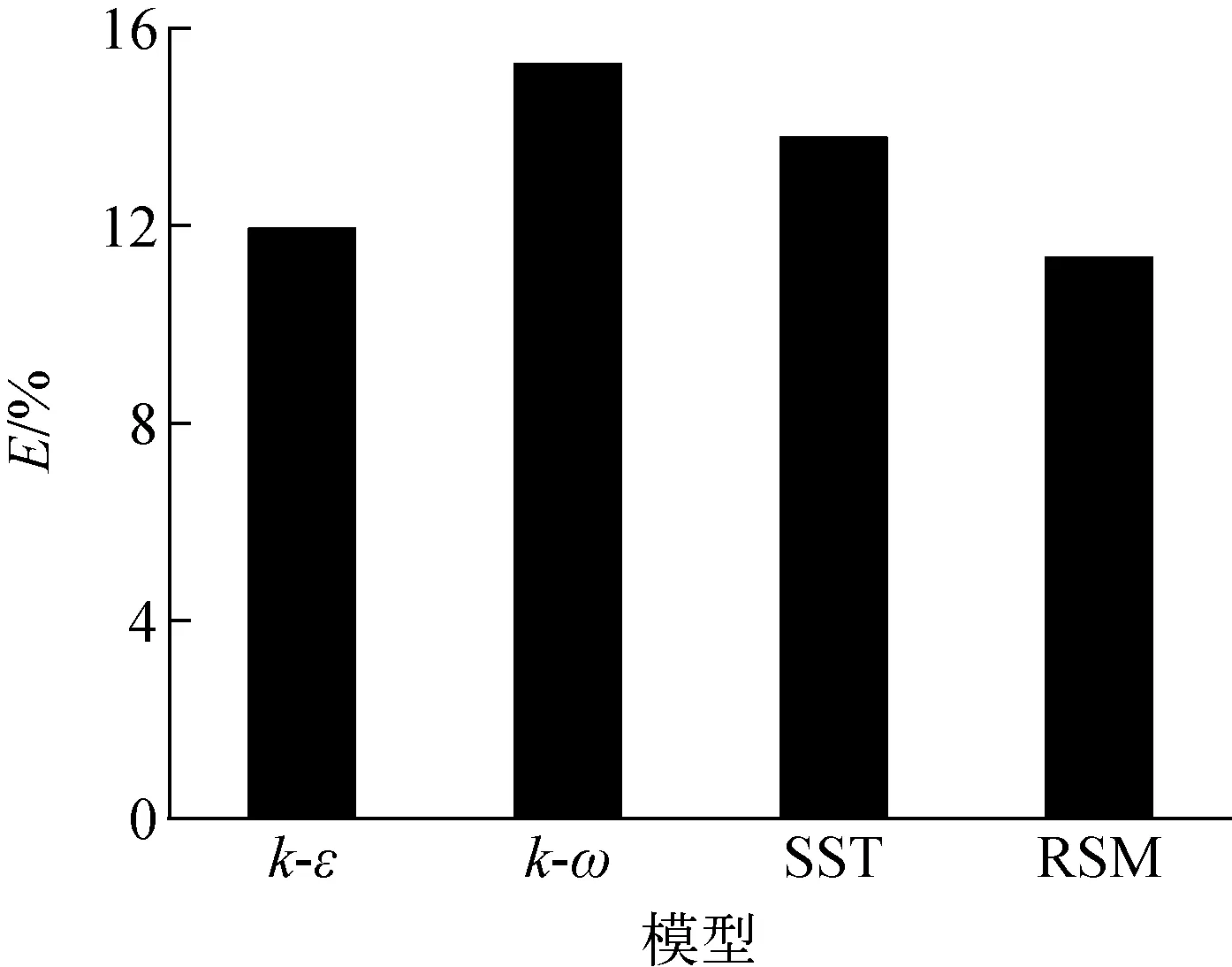
图11 各模型模拟氦气外掠圆柱流动的均方根偏差Fig.11 Root mean square deviation of different turbulence models for helium gas flowing over cylinder

在ANSYS Fluent程序求解湍流流动的能量守恒方程时，一般认为速度场和温度场可比拟，并通过引入湍流普朗特数Prt计算湍流导热系数，即：

(11)

式中：μt为湍流黏性系数；λt为湍流导热系数。

研究过程中Prt取ANSYS Fluent程序的默认值0.85。根据式(11)可知，湍流模型计算的湍流黏性系数越高，湍流导热系数越大，则湍流换热越强，等效表面热流密度越大。故而不同湍流模型计算的等效表面热流密度差异直接取决于湍流模型计算的湍流黏性系数。

3组实验数据与数值模拟结果的对比结果(图6b、8、10)表明：采用不同湍流模型计算的等效表面热流密度均低于实验值，这可能是由于瞬态加热过程中壁面附近流体发生扰动强化了湍流换热，而该强化作用在数值模拟中并未考虑。均方根偏差计算表明，ε类湍流模型与实验值吻合度更高，明显优于ω类湍流模型，这是由于两类湍流模型求解的湍流黏性系数不同所致。

3 夹持铜片对实验结果的影响

由于实验过程中金属铂的壁面热流密度无法直接测量，Liu等[7-9]通过加热功率与金属铂的温度进行计算，间接获得其值。然而实验过程中金属铂不仅对流体进行加热，同时与两侧的夹持铜片发生热传导，若直接采用数值模拟所获得的表面热流密度与实验值进行对比，将会因为忽略与铜片的导热而产生较大误差。为此，在上述数值模拟与实验结果的对比过程中，表面热流密度均采用等效表面热流密度，即通过式(9)计算获得。根据氦气外掠平板流动实验(实验工况为：流体速度10 m/s，气体入口温度313 K，功率指数增长周期92 ms)的数值模拟结果，金属铂真实表面热流密度与等效热流密度的对比示于图12。可看出，两者存在约20%的相对偏差。即当前的热负载功率指数提升实验平台可通过间接比较等效热流密度的方法对瞬态条件下对流传热特性进行一定程度的验证，但等效热流密度计算方法无法剔除夹持铜片导热引入的误差。为更好地验证瞬态条件下的对流传热特性，有必要对该实验平台进行一定的改进。

图12 金属铂的真实表面热流密度与等效表面热流密度对比Fig.12 Comparison between actual surface heat flux and equivalent surface heat flux of platinum

4 结论

通过ANSYS Fluent程序，针对功率指数提升实验平台建立分析模型，选取标准k-ε模型、标准k-ω模型、过渡SST模型及RSM模型4种湍流模型，通过控制y+<1确保所有模型均采用强化壁面处理，对瞬态过程中的流固耦合换热进行了分析，得到以下结论。

1) 热负载指数提升过程中，热功率一部分用于对流换热而另一部分仍留在固体内，且对流换热占热功率的比值与热功率的提升速率有关，热功率提升速率越高，对流换热的占比越低。

2) 瞬态加热过程中，加热壁面附近流体由于温度的瞬变进而引起密度与黏性的变化，其流体速度与温度分布将不断发生变化，即定热物性假设与壁面函数法不适用于流体热物性随温度显著变化的瞬态对流传热特性的分析。

3) 采用4种湍流模型模拟的等效表面热流密度均低于实验值。均方根偏差计算表明，ε类湍流模型的模拟结果与实验值吻合度较高，且明显优于ω类湍流模型。

4) 当前的热负载功率指数提升实验平台可通过间接比较等效热流密度的方法对瞬态条件下的对流传热特性进行一定程度的验证，但等效热流密度计算方法无法剔除夹持铜片导热引入的误差。为更好地验证瞬态条件下的对流传热特性，有必要对该实验平台进行一定的改进。