石墨慢化通道式熔盐堆的稳态热工水力计算模型

何 龙，余呈刚,，郭 威,*，戴 叶,，王海玲,，蔡翔舟,*

(1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院 先进核能创新研究院，上海 201800；3.中国科学院大学，北京 100049)

熔盐堆的一种典型设计是堆内含有石墨慢化材料[1-2]，堆芯由截面为六边形或四边形的石墨组件规则排布构成。燃料盐在各组件的熔盐通道内流动并发生裂变反应。石墨慢化通道式熔盐堆与传统反应堆在传热上有很大不同。首先，体现在堆芯裂变功率主要沉积在液态熔盐中，并由熔盐自身的流动带出堆芯。其次，由于中子和伽马射线的辐照，堆芯固体区域(石墨慢化材料和结构材料)仅沉积了少量能量。最后，燃料盐在组件的熔盐通道内沿轴向流动，不同组件内熔盐没有通过横向流动产生的质量、能量和动量的交换，组件间热量传递依赖于石墨慢化材料的热传导实现。

对于石墨慢化通道式熔盐堆，现有稳态分析模型[3-4]及瞬态分析程序(如DYN3D-MSR[5]和TANG-MSR[6]程序)通常采用并联多通道模型。该模型将堆芯内不同区域的组件等效为独立的空心圆柱，采用一维流体模型和一维热传导方程描述熔盐和圆柱壁面的传热。模型仅考虑圆柱壁径向的热传导，未能考虑组件间的传热。由于并联多通道模型在物理模型上进行了大量简化，这导致该模型无法计算熔盐堆内反射层的温度分布，同时也无法考虑组件间的热耦合。

为克服并联多通道模型面临的限制，本文针对石墨慢化通道式熔盐堆将建立一种新型稳态热工水力学模型(STHM-MSR, steady-state thermal-hydraulic model for molten salt reactor)。STHM-MSR耦合固体区域的三维热传导方程和一维流体模型，可考虑组件间由于热传导产生的热交换，并能计算反射层的温度分布。为验证STHM-MSR对温度和流量分配计算的正确性，本文将对比RELAP5程序的计算结果。基于2 MWt液态燃料熔盐堆的一种概念设计，本文将计算在额定功率下堆内的稳态温度分布和流量分配。

1 物理模型

STHM-MSR采用三维热传导方程计算堆芯内石墨组件和反射层等固体区域的温度分布，计算方程如下：

(1)

式中：λg、Tg和Qg分别为固体材料的热导率、温度和沉积的热源。固体区域的外表面采用绝热边界条件，熔盐通道壁面采用对流换热边界条件。通道内熔盐采用一维单相流体模型，求解质量守恒方程、动量守恒方程和能量方程：

(2)

(3)

(4)

式中：ρ、ν、Tf和cf分别为熔盐的密度、速度、温度和比热容；pf为通道内的摩擦压降；A为通道的流体面积；Qf为熔盐的内热源；Qh为熔盐与通道壁面产生的换热量。一维单相流体模型采用指定入口温度和入口质量流量边界条件。

堆芯固体区域的三维温度场通过壁面的对流换热边界条件与熔盐温度建立了热耦合，通道壁面的热流密度计算公式为：

(5)

式中：λf和De分别为熔盐的热导率和通道的水力学直径；Nu为努塞尔数。Nu的计算关系式采用熔盐在光滑圆管内强迫对流换热的实验结果[7](表1)。表1中，Re为雷诺数，Pr为普朗特数，L为通道的长度，μf和μs分别为基于熔盐温度和壁面温度计算得到的熔盐黏度。对q(x,y,z)沿通道换热湿周积分可得式(4)中的Qh：

(6)

图1为固体区域温度和一维流体温度建立热耦合的示意图，计算模型中每个壁面与通道内熔盐将建立映射关系，并通过式(5)和式(6)计算固体和流体在壁面的热交换。

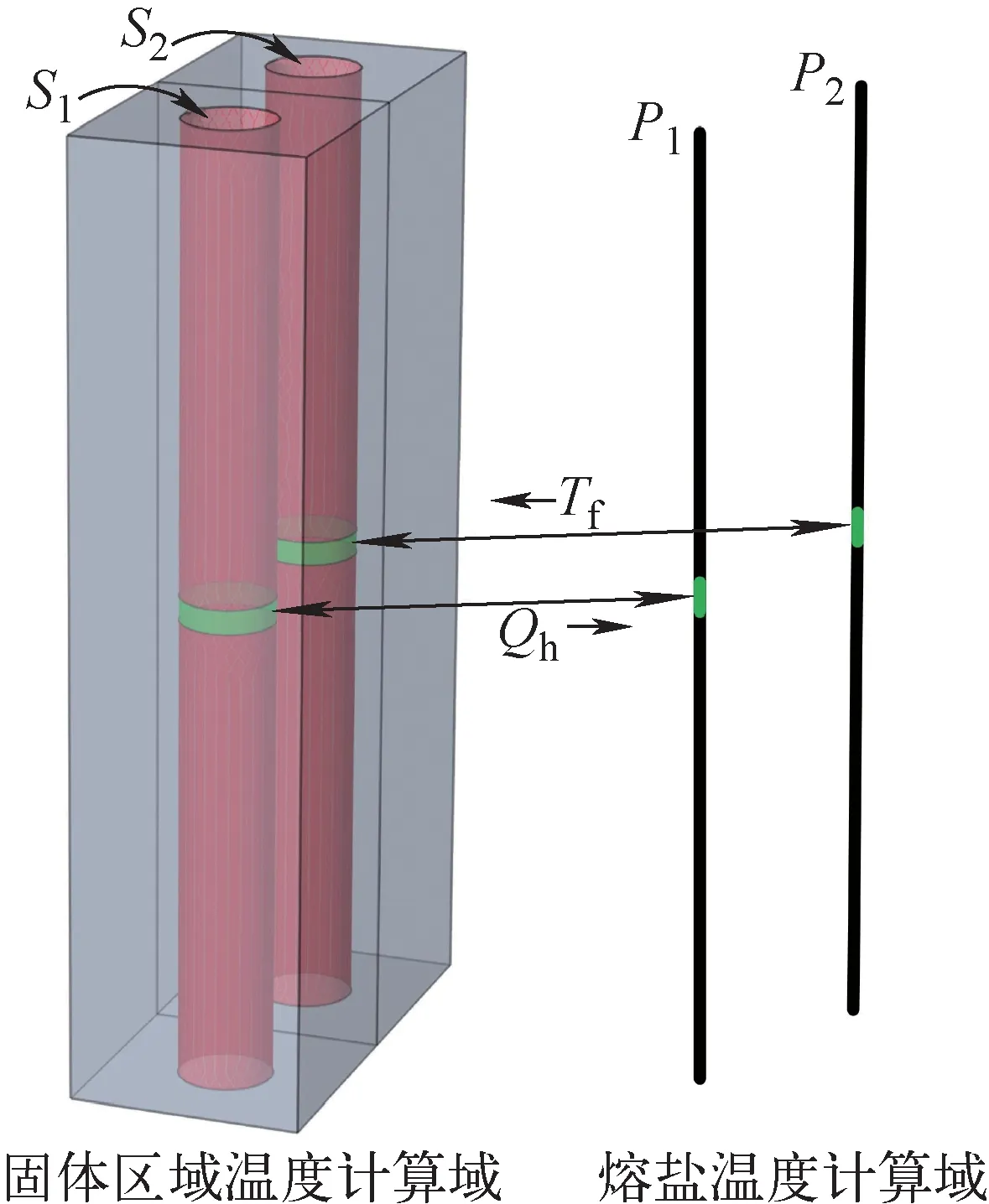
图1 固体区域温度与一维熔盐温度耦合示意图Fig.1 Schematic diagram of coupling between solid temperature and molten salt temperature

对动量方程沿通道轴向进行积分，可得到通道内的压降方程：

Δpa,i=Δpi-Δpf,i-Δpg,i-Δpk,i

(7)

式中：Δpa,i、Δpi、Δpf,i、Δpg,i和Δpk,i分别为通道i的加速压降、总压降、摩擦压降、提升压降和局部压降(上下腔室的形阻)，计算公式如下：

(8)

(9)

(10)

(11)

式中：mi为通道i中的质量流量；f和k分别为摩擦系数和形阻系数，计算中每个通道需输入各自的k。式(8)～(11)中质量流量、密度及速度均为给定入口温度和流量边界下计算得到的已知量。在计算出各种压降后，根据式(7)可得通道i的总压降Δpi。由于各通道的进口和出口分别与相同的腔室相连接，根据平行通道压力损失相等的原则，合理的质量流量分配将使各通道的总压降Δpi相同。以通道流通面积为权重的堆芯平均压降Δpav可表示为：

(12)

图2 STHM-MSR计算流程Fig.2 Calculation flow of STHM-MSR

流量分配计算步骤[8]如下：1) 假定各通道的初始质量流量mi；2) 在给定mi情况下计算固体区域的温度分布和各通道内熔盐轴向的温度、速度和密度分布，并以此计算各通道的Δpi和Δpav；3) 根据各通道的Δpi和Δpav的偏差重新调节各通道的mi(调节过程需保证堆芯的总质量流量守恒)；4) 重复步骤2，直到满足|Δpi-Δpav|/Δpav<ε条件。图2示出了STHM-MSR计算流程。

STHM-MSR包含了固体区域三维热传导计算、一维流体换热计算及各燃料通道间流量分配计算。其中三维热传导和一维流体模型由COMSOL Multiphysics程序[9]进行求解，而固体区域温度和流体温度的耦合以及通道间流量分配计算则基于编写的MATLAB脚本实现。STHM-MSR实现了固体区域三维温度场与一维流体的耦合，解决了并联多通道模型不能考虑组件间传热等方面的不足。该模型适用于在流体处于液相情况下，通道式结构堆芯的稳态热工水力学分析。

2 热工水力学模型验证

考虑到目前没有商用程序采用与STHM-MSR完全相同的物理模型，本文采用RELAP5程序[10]对STHM-MSR进行验证。

固体区域温度和流体温度计算结果采用单个空心圆管进行验证。空心圆管长为50 cm，内径为2 cm，管壁厚度为1 cm，管壁热导率为25 W/(m·K)。圆管总共沉积了59 650.0 W热量，其中4%均匀分布在管壁，剩余部分沉积在冷却剂内。圆管由FLiBe熔盐冷却，质量流量为0.5 kg/s，入口温度为873.15 K。由于圆管管壁较薄且由冷却剂强迫对流冷却，管壁轴向的热传导并不显著，因此圆管管壁的三维热传导问题可近似为一维径向热传导问题。RELAP5程序对于固体区域采用一维热传导模型，对于该验证模型，RELAP5程序对管壁温度的计算结果可很好地验证三维热传导模型。验证计算过程中，STHM-MSR采用RELAP5程序内置的FLiBe物性及相同的换热关系式。

图3a对比了圆管底部(z=2.5 cm)、中间(z=25.0 cm)及顶部(z=47.5 cm)位置处管壁径向温度分布。由于管壁轴向热传导效应不明显，STHM-MSR计算结果与RELAP5程序计算结果基本一致。FLiBe熔盐沿轴向的温度分布如图3b所示，STHM-MSR和RELAP5程序的计算结果一致。图3c示出了STHM-MSR计算得到的管壁的三维温度分布和熔盐的轴向温度分布。

为验证流量分配及流量分配对温度的影响，采用3个相同尺寸的竖直圆管(圆管的尺寸与温度验证的圆管相同)作为计算模型。各圆管沉积的不同热源值列于表2，总的入口质量流量为0.075 kg/s，入口温度为873.15 K。为保证各圆管的总压降相同，合理的流量分配将使各管道内的重力压降加上其他形式压降的总和相同。从表2可看出，RELAP5和STHM-MSR计算得到的各圆管内的流量分配和出口熔盐温度符合很好。

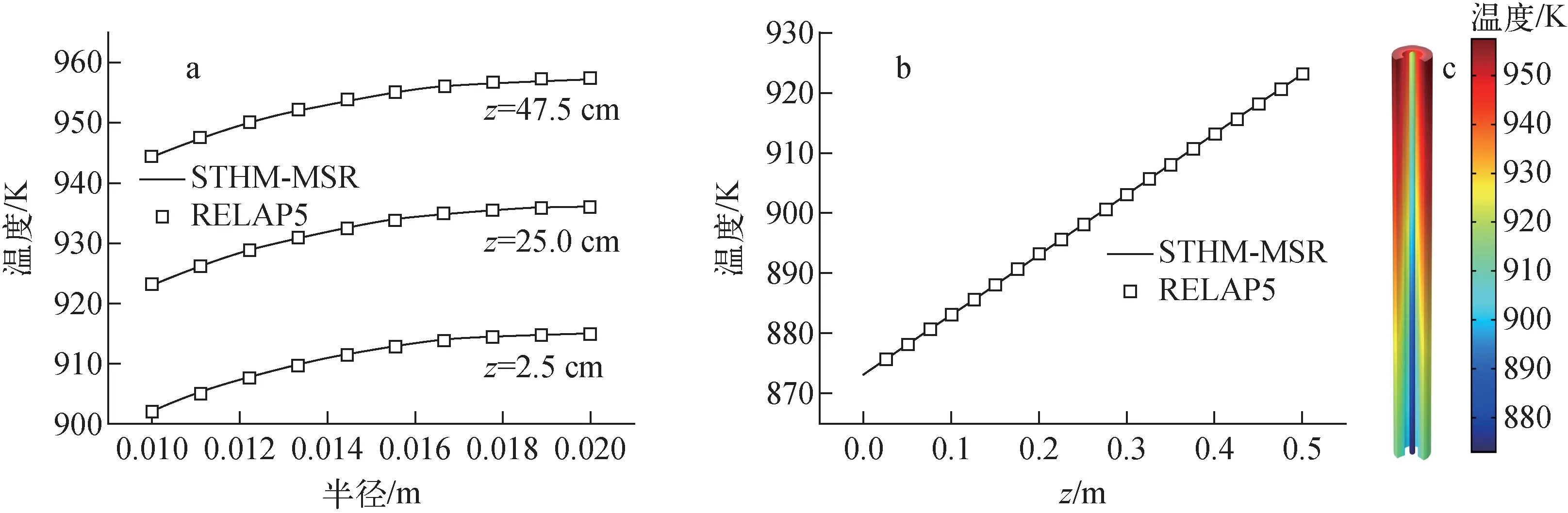
图3 圆管内温度分布Fig.3 Temperature distribution in circular tube

圆管编号功率/W102质量流量/(kg·s-1)出口熔盐温度/KRELAP5STHM-MSRRELAP5STHM-MSR12 982.52.509 832.510 16922.953 8922.947 123 579.02.891 462.892 17925.026 6925.013 732 386.02.098 702.097 67920.798 2920.821 3

3 2 MWt液态燃料熔盐堆堆芯稳态热工水力分析

3.1 计算模型

2 MWt液态燃料熔盐堆[11]是由中国科学院上海应用物理研究所提出的小型熔盐实验堆(简称实验堆)。图4a和b为实验堆的纵向和横向剖面图，堆芯由85个横截面为六边形的石墨组件组成，组件的尺寸如图4c所示。实验堆热功率为2 MW，进出口温度分别为600 ℃和620 ℃。堆芯额定流量为59.25 kg/s，其中大部分熔盐流经堆芯活性区，少量熔盐流经外围熔盐层。

图4 实验堆和计算模型的示意图Fig.4 Schematic diagrams of experimental reactor and calculation model

堆芯内功率分布由SCALE程序计算[12]得到，表3为实验堆不同区域内沉积的总功率份额。熔盐堆中缓发中子先驱核及衰变热会随燃料流动发生迁移，这对堆芯内功率分布会有轻微影响，目前SCALE计算结果未能考虑燃料盐流动对功率的影响。

表3 功率分布Table 3 Power distribution

注：1) 外围熔盐层顶部、径向和底部区域功率份额分别为0.99%、2.39%和1.03%

由于实验堆堆芯具有1/12对称性，计算模型采用1/12堆芯。计算模型的横截面如图4d所示，图中根据各组件的径向位置对其进行了编号。计算模型包含活性区、径向反射层、径向部分的外围熔盐层和反应堆容器。各通道及外围熔盐层均等效为一维流体，并给定入口温度和质量流量边界条件。外围熔盐层中质量流量的设计值为5%的堆芯额定流量，计算过程中外围熔盐层入口流量采用该值，流量分配计算只针对带有编号的组件。各通道的入口温度计算公式为：

T=Q/Mcf+Tin

(13)

式中：Q为下腔室及熔盐通道和下反射层内沉积的总功率；M为熔盐的质量；Tin为堆芯的入口温度。实验堆的上下腔室对优化流量分配起重要作用。由于缺乏流量分配的水力学实验，目前无法获得各通道的形阻系数k，计算中忽略了由于上下腔室造成的局部压降。

3.2 计算结果与讨论

图5为堆芯内固体区域及各通道内熔盐的温度分布。由于石墨内沉积的功率由通道内熔盐带走，石墨的温度会高于通道内熔盐的温度。反射层内沉积的热量依赖外围熔盐层和堆芯边缘处的熔盐通道冷却，这导致反射层两侧的温度更低。实验堆内温度峰值出现在反射层，高达642.3 ℃。由于固体区域内沉积的功率份额较少，熔盐和石墨的温差并不显著。

图6a示出了z=0.2，0.55和0.9 m处平面上的温度分布，图6b示出了这3个平面上的等温线分布。对于堆芯中心区域的组件，等温线呈现以熔盐通道为中心的同心圆分布，这说明组件之间的传热并不显著。边缘处的组件(编号9～11，图4d)对反射层起冷却作用，这导致这些组件内的等温线明显偏离同心圆分布。

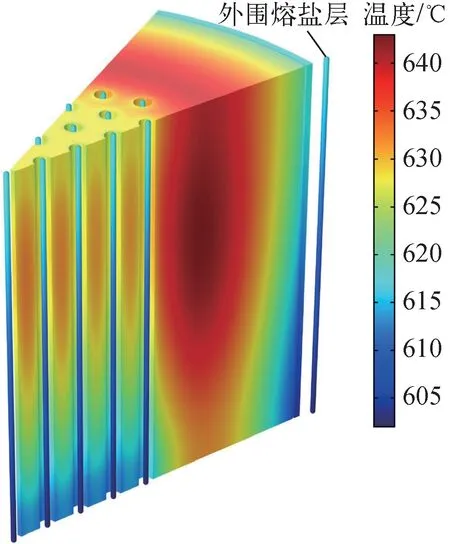
图5 堆芯温度分布Fig.5 Temperature field of reactor core

表4列出了功率、流量和出口温度统计。由表4可知，各组件的出口温度偏差较小，组件间流量分配较为平均。ΔE为通道内熔盐带走的功率(基于熔盐进出口的温差)与对应组件内沉积功率的差值，体现了某组件通过热传导带走邻近组件热量的能力。对于中心区域的组件，由于沉积的功率较大，会通过邻近组件带走部分功率，这体现在ΔE为负值。对于组件1～8，ΔE的绝对值仅为几十W，这说明这些组件间的热传递不显著。对于边缘组件9～11，ΔE显著大于0，这是由于这些组件会带走少部分反射层内沉积的功率。由表4还可知，外围熔盐层的ΔE高达1 847.4 W，这表明外围熔盐层带走了反射层和反应堆容器内沉积的大部分功率。对各通道内熔盐带走的功率乘以权重因子并求和，可得到在1/12堆芯模型中熔盐带走的总功率。熔盐带走的总功率(121 550.8 W)与1/12堆芯计算域内沉积功率(121 550.9 W)仅偏差0.1 W，这表明STHM-MSR的计算结果满足能量守恒。

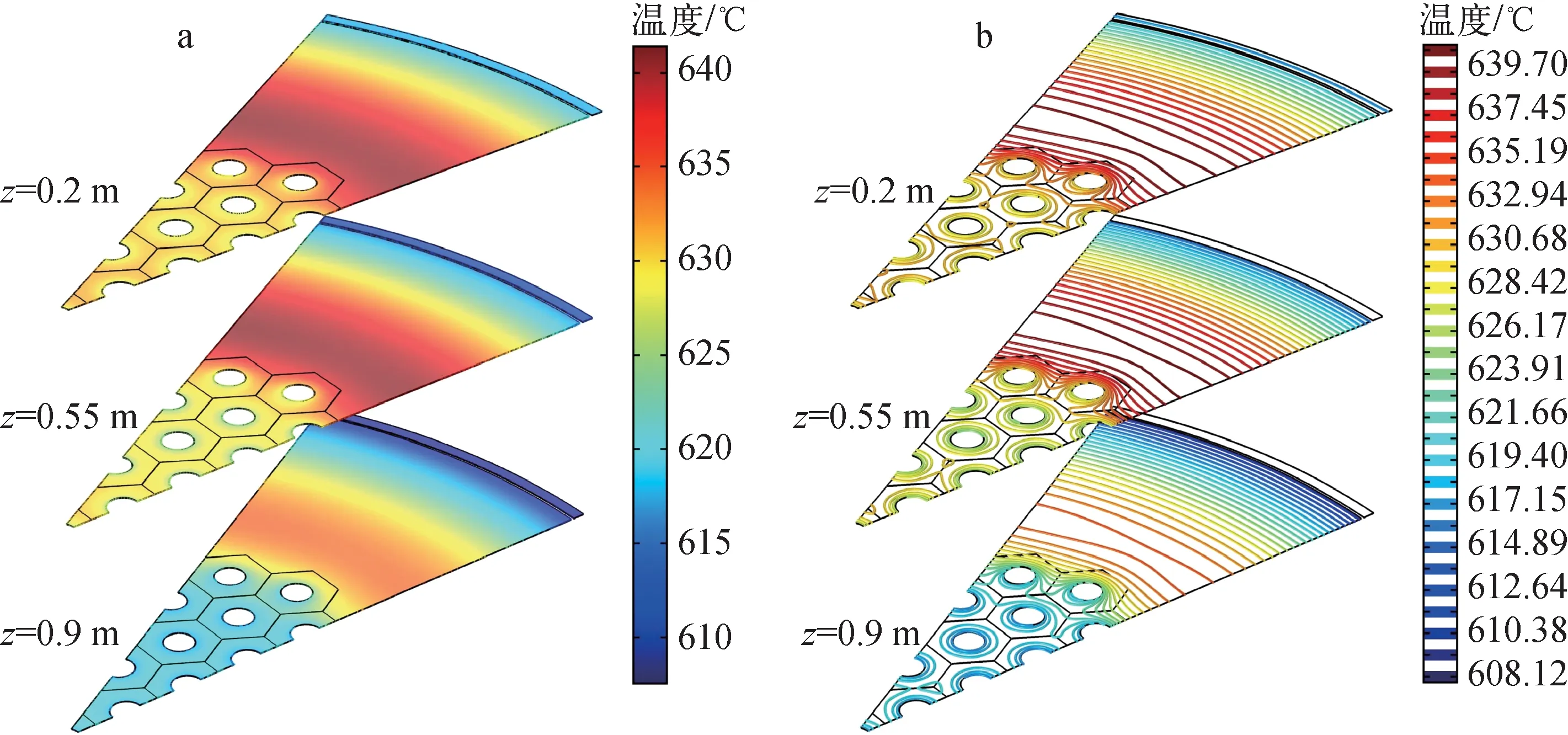
图6 z=0.2, 0.55和0.9 m处平面上的温度及等温线分布Fig.6 Cross-sectional view of temperature field and isotherms at cut planes of z=0.2, 0.55 and 0.9 m

组件编号权重因子沉积功率1)/W流量/(kg·s-1)出口温度/℃ΔE/W11/1218 031.6 0.712 2617.572-16.5 21/217 777.8 0.703 4617.545-17.6 31/216 984.7 0.680 8617.362-5.3 41/216 984.7 0.680 6617.360-12.1 5115 878.9 0.649 1617.09517.9 61/215 878.9 0.649 2617.09520.3 71/215 318.5 0.633 8616.96663.3

续表4

注：1) 组件沉积功率包含石墨和熔盐内功率的总和，外围熔盐层沉积功率仅表示熔盐内的功率

4 结论

针对并联多通道模型的不足，本文针对通道式熔盐堆建立了一种新型堆芯稳态热工水力学模型STHM-MSR。STHM-MSR耦合了固体区域的三维热传导模型及一维单相流体模型，可计算组件间的传热和反射层内的温度分布。通过对比STHM-MSR和RELAP5程序计算得到的温度和流量分配结果，验证了STHM-MSR的正确性。

应用STHM-MSR，分析了2 MWt液态燃料熔盐堆堆芯内的温度分布和流量分配。计算结果表明：1) 实验堆内各组件的出口熔盐温度和流量分配较为均匀；2) 堆芯中心区域组件间的热耦合并不显著，这些组件间基于热传导传递的热量小于100 W；3) 外围熔盐层带走了反射层内大部分的热量，对反射层的冷却起至关重要的作用。