基于虚拟信号注入的MTPA控制稳态误差分析
2019-02-25王建民
张 鹏,王建民
(山东大学,济南 250061)
0 引 言
内置式永磁同步电机(以下简称IPMSM)具有体积小、效率高、功率因数高等优良特性,近年来得到广泛的应用[1]。为了实现对IPMSM的高效控制,常采用最大转矩电流比(以下简称MTPA)控制策略。
理论上,根据电机参数可以直接计算出MTPA工作点,从而进行MTPA控制[2],该方法在电机参数恒定时是比较准确的,然而在电机实际运行过程中,受到磁饱和、温度等因素影响,参数会发生变化。为了解决此问题,许多学者将查表法和参数辨识法应用在MTPA控制中[3-4]。前者需要进行离线测试等预先准备工作,其准确度仍然会受温度、材料属性、制造工艺等因素的影响,并且需要占用额外的存储资源。后者不需要预先了解电机参数,但该算法需要进行较繁杂的运算,使系统变得更复杂,动态性能相对较差。为了减小电机参数变化带来的影响,还有学者提出了电流矢量角自校正法[5]。该方法避免了控制系统对电机参数的严重依赖性,但在变负载情况下控制系统的动态性和稳定性很难保证。
近年来,出现了一种基于高频电流信号注入的MTPA新方法[6-7]。通过向电机的定子绕组中注入高频小电流信号,依据在MTPA工作点处电磁转矩对电流角的变化率为零的原理(如图1所示),实时追踪MTPA工作点。由于在实际应用中很难直接测量电机的转矩,有学者提出通过测量转速来代替转矩[6],然而这种算法对速度传感器的精度有很高的要求。在文献[7]中,通过计算输入功率来代替计算或测量转矩。此类方法注入了实际的高频电流,无法避免由此产生的转矩脉动、高频噪声、附加损耗等问题。针对实际高频信号注入MTPA控制策略中存在的问题,文献[8]提出了虚拟信号注入法。该方法不需实际注入高频电流信号,有效地避免了转矩脉动、附加损耗等问题。然而在最终算法中,电磁转矩的计算仍包含定子电阻、d轴电感,当这些参数与电机的实际值不一致时,便会产生MTPA控制误差。
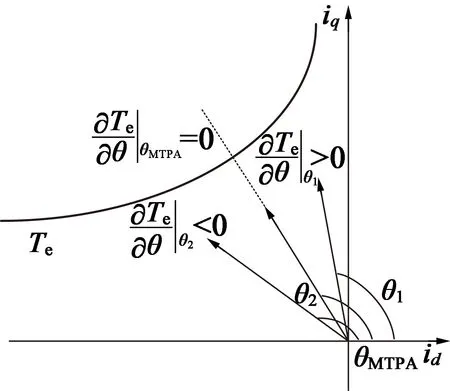
图1 恒转矩曲线和MTPA工作点
本文对虚拟信号注入法MTPA控制的稳态性能进行了研究。推导了由参数偏差引起的MTPA误差角表达式,在此基础上对定子电阻和d轴电感偏差引起的MTPA误差角进行了一系列的理论分析和仿真研究,为今后采取措施提高虚拟高频注入法的控制精度,提供了理论依据。
1 基于虚拟信号注入的MTPA控制原理
1.1 IPMSM的MTPA控制
在转子参考坐标系dq中,IPMSM的动态电压方程:
(1)
式中:ud和uq分别为d,q轴电压;id和iq为d,q轴电流;Ld和Lq分别为d,q轴电感;ωr为转子的电角速度;Rs为定子电阻;λf为永磁体磁链。
相应的电磁转矩方程为:
(2)
式中:p为极对数。IPMSM的电磁转矩可以分为永磁转矩和磁阻转矩两部分。前者与q轴电流成正比,后者与d轴电流和q轴电流的乘积成正比。若定子电流矢量的幅值为Is,空间位置角为θ,则式(2)可表达:
(3)
由图1的恒转矩曲线可知,对于特定的转矩总会存在一个最优电流角使电流幅值最小,这一工作点即为MTPA工作点。MTPA工作点为恒转矩曲线的切点,也是恒转矩曲线上距离坐标原点最近的点。根据极值原理可得,在MTPA工作点处∂Te/∂θ等于零,即:
(4)
由式(4)可求出与MTPA工作点对应的最优电流角θMTPA:
(5)
1.2 高频信号注入法MTPA控制原理
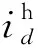
式中:idf和idh分别为d轴电流中的基波分量和高频分量;iqf和iqh分别为q轴电流中的基波分量和高频分量。
注入高频电流后的电磁转矩表达式:
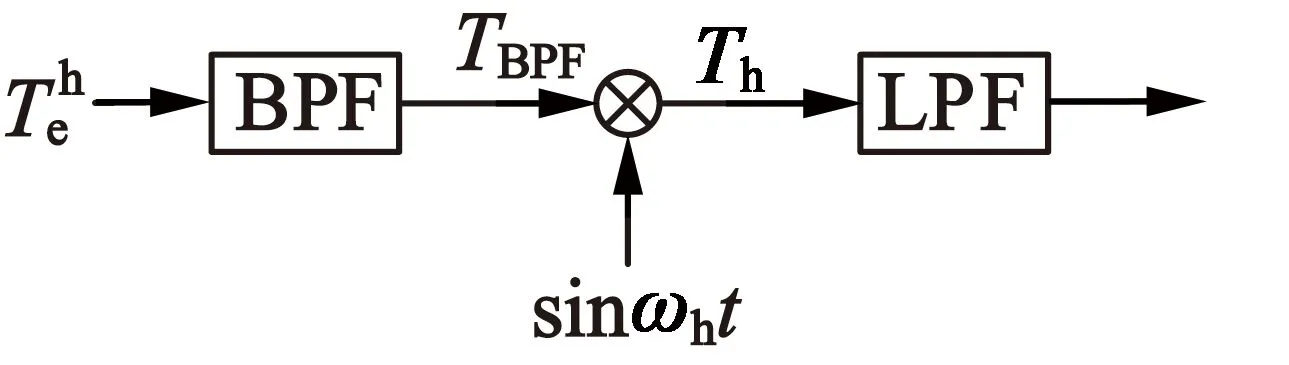
图2 MTPA判据的提取
分量。剩余量TBPF乘上sin(ωht)后,再通过低通滤波器,最终得到的MTPA判据,To表达式如下。
(9)
通过MTPA控制器,对To进行积分,其输出作为电流矢量角给定值θ*。稳态时应有To=0,此时控制器的输出就是最优电流角(MTPA电流角)。
1.3 虚拟信号注入法MTPA控制原理
在虚拟信号注入法中,并不需要在电机定子绕组中实际注入高频电流。而是利用d,q轴电压和电流的稳态值,根据电机稳态电压方程,获得λf和Lq参数,进而计算假如有高频电流注入所产生的电磁转矩,并从中提取MTPA控制信号。
考虑到稳态时电流变化率为零,由式(1)可得:
(10)
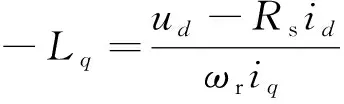
将式(10)和式(11)代入式(8),可以计算出有高频电流注入时的电磁转矩为:
(12)

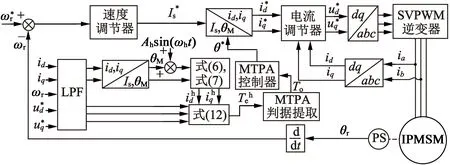
图3 虚拟信号注入法MTPA控制系统
2 虚拟信号注入法MTPA控制的稳态误差分析
2.1 稳态误差公式
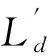
根据电机d,q轴稳态电压方程,式(13)可进而表示:
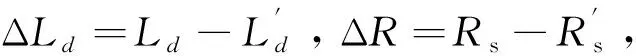
(15)
其中:
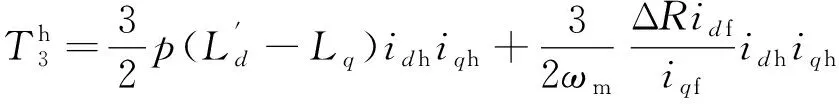
①设置相似度阈值T,记录关键帧的数组为keyFrame[n],其中n为动态行为关键帧数。初始化循环变量i=0,将起始帧作为关键帧保存到keyFrame[0],并将第2帧记为当前帧;
稳态时To应为零,因此有:
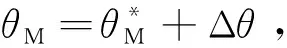
(22)
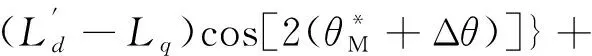
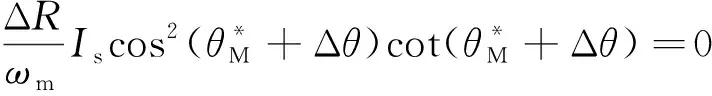
考虑到Δθ很小,所以cos Δθ≈cos(2Δθ)≈1,sin Δθ≈Δθ,sin(2Δθ)≈2Δθ,由式(23)可求出误差角公式:
(24)
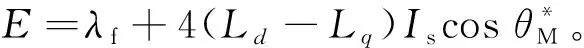
根据式(24),若ΔR,ΔLd均为零,则理论上误差角Δθ应为零。这是因为若算法中的Rs和Ld与实际值一致,由式(10)、式(11)估算得到的λf和Lq参数为准确值,则由它们计算出的电磁转矩也是准确的,在此理想条件下该方法能够实现精确的MTPA控制。反之,若算法中的Rs和Ld与电机的实际值出现偏差,由它们估算出的λf和Lq参数就会出现偏差,进而产生MTPA控制角误差。
2.2 仿真结果与分析
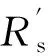

表1 电机参数
2.2.1 由ΔR引起的稳态误差
假定ΔLd=0,仅考虑由ΔR引起的误差,此时式(24)变为:
(25)
图4给出了不同转速下由ΔR引起的误差角的仿真和计算结果。由图4可见,式(23)和式(24)的计算结果重合,误差角公式计算结果与仿真结果基本一致。当ΔLd=0时,由ΔR单独引起的误差角随着ΔR绝对值的增大而增大。由于式(25)的分母中ωrE项随转速降低而减小,因此转速越低,误差角就越大。但总体来看,由电阻偏差引起的角度误差很小。
(a) 转速1 000 r/min时由ΔR引起的误差角
图4不同转速下由ΔR引起的误差角
2.2.2 由ΔLd引起的稳态误差
假定ΔR=0,仅考虑由ΔLd引起的误差,此时式(24)变为式(26)。
(26)
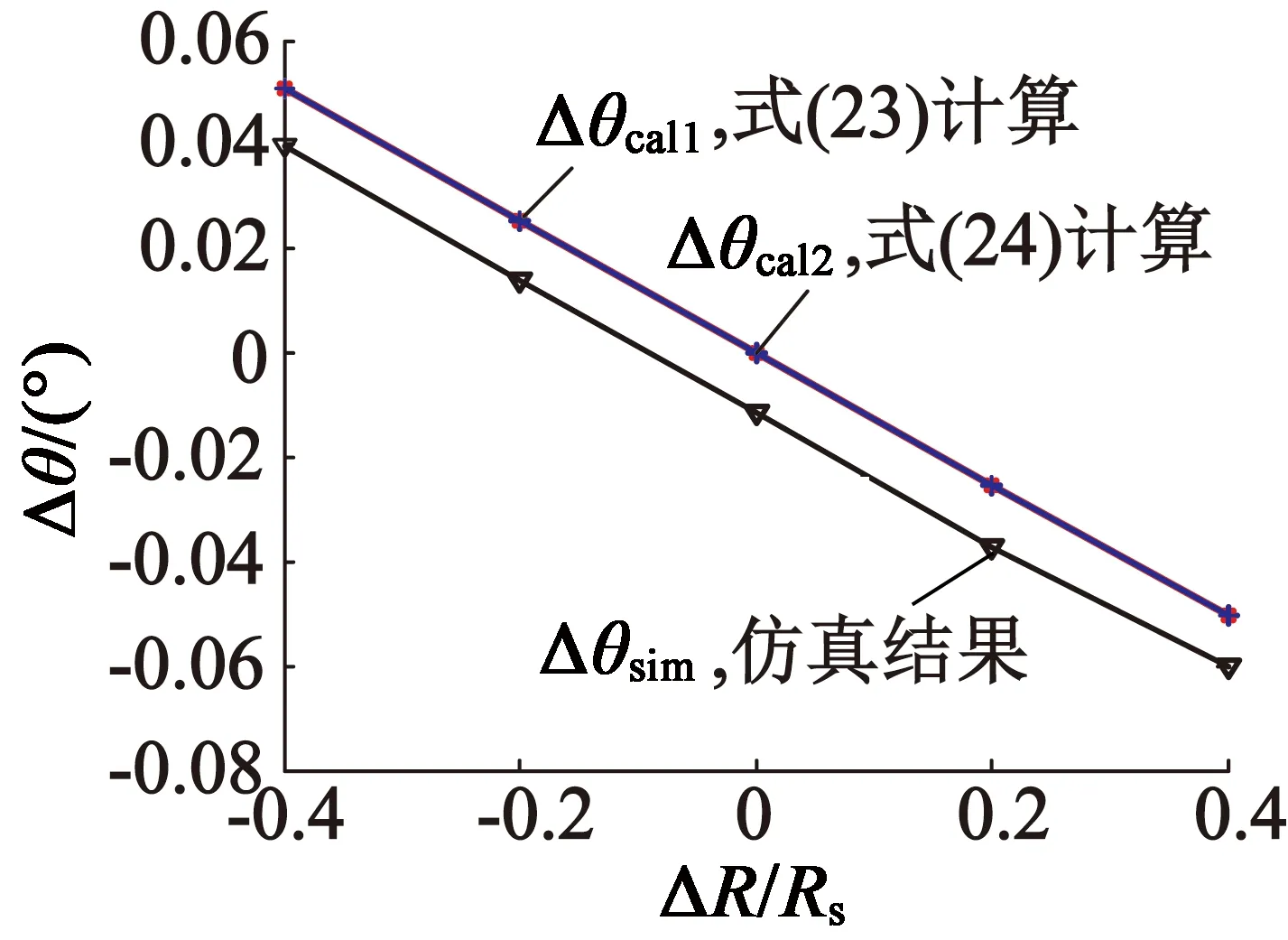
图5给出了不同转速下由ΔLd引起的误差角的仿真和计算结果。由图5可见,3条曲线重合,误差角公式计算结果与仿真结果基本一致。由于分母中与ΔLd有关项在数值上通常远小于与ΔLd无关项,所以当ΔR=0时,由ΔLd单独引起的误差角近似与ΔLd成正比,而且当ΔLd较大时会产生显著的误差角。因此d轴电感偏差是引起MTPA误差的主要原因。另外,由ΔLd单独引起的误差与转速无关。
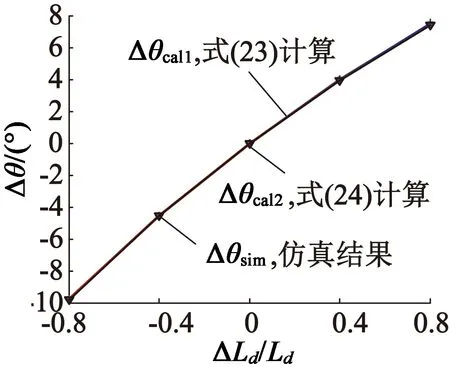
(a) 转速1 000 r/min时由ΔLd引起的误差角
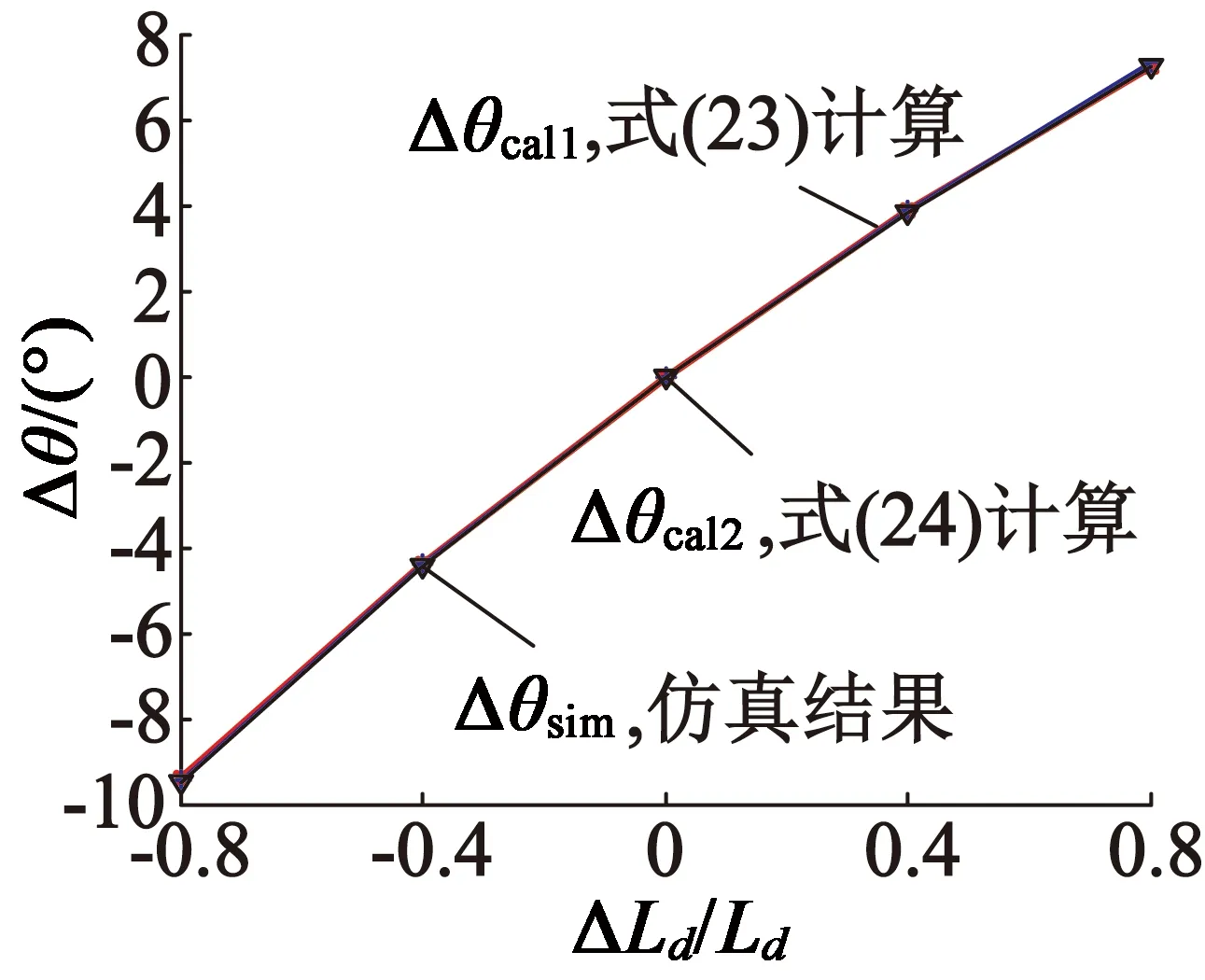
(b) 转速100 r/min时由ΔLd引起的误差角
图5不同转速下由ΔLd引起的误差角
2.2.3 ΔR,ΔLd极性对误差角的影响
在转速不是很低的情况下,由于式(24)分子中ΔR项与ΔLd项相比要小得多,分母中也以ωrE项为主要分量,所以ΔR对误差角影响很小,但随着ΔR与ΔLd极性配合不同,会对误差角产生不同影响。作为例子,表2给出了转速为100 r/min下ΔR/Rs,ΔLd/Ld分别为0.4时的误差角情况。
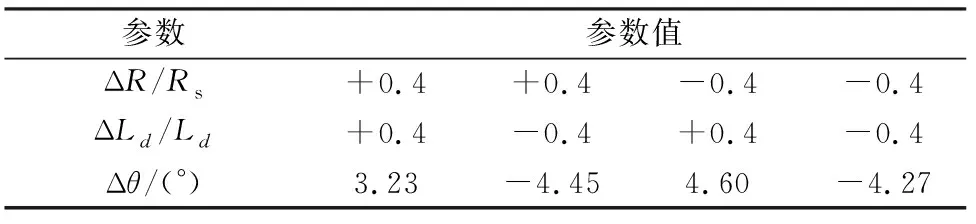
表2 ΔR,ΔLd极性对误差角的影响
文献[9]中还给出了虚拟信号注入法的另一种算法。
(27)
(28)
图6给出了不同转速、不同ΔR下误差角的仿真和计算结果。显然,该算法的误差角始终比较大。如前所述,d轴电感偏差ΔLd是产生MTPA误差的主要原因,而该算法是式(13)算法中ΔLd=Ld的情况,因此在ΔLd (a) 转速1 000 r/min时的误差角 (b) 转速100 r/min时的误差角 图6采用式(27)算法时不同转速下的误差角 本文对虚拟信号注入法IPMSM的MTPA控制稳态性能进行了研究。在基于虚拟信号注入的MTPA控制中,不需要在定子绕组中实际注入高频电流信号,而是利用电压电流检测值计算假如有高频电流信号注入时,将会产生的高频电磁转矩,并从中提取MTPA判据,进而实现对MTPA工作点的自动追踪。由于算法中包含定子电阻和d轴电感,当这些参数与电机实际值出现偏差,就会导致MTPA控制角产生误差。本文推导了由参数偏差引起的MTPA误差角表达式,在此基础上对定子电阻和d轴电感偏差引起的MTPA误差角进行了一系列的理论分析和仿真研究。结果表明:所推导的误差角公式具有较高的精度;在运行转速不是很低的情况下,由电阻偏差引起的误差角不大;d轴电感偏差是产生MTPA误差角的主要原因,如果d轴电感偏差较大,会致使MTPA误差角显著增大。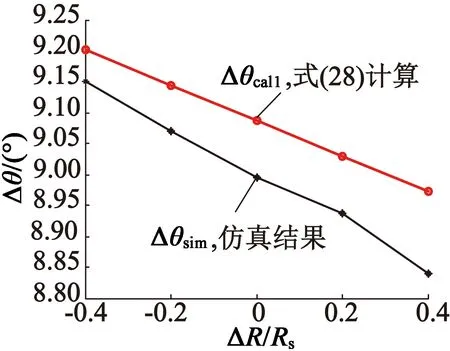
3 结 语
