基于SPC1068的步进电动机可控转矩矢量控制

吕常智，韩 鲁

(山东科技大学，青岛 266590)

0 引 言

步进电动机的工作原理是将电信号转化为角位置。电机转速及转子位置，只与脉冲频率和数量相关[1]。随着步进电动机工作环境复杂化，电机低速振荡和失步问题更加突出。对于电机振荡和失步问题，国内外学者的研究主要集中在细分电流控制[2-8]和电机速度轨迹控制[9-12]两方面。在特定的场合下，电机低频振荡和失步问题得到有效抑制。

步进电动机振荡和失步现象可通过控制转矩得到解决。通过矢量控制能对步进电动机转矩进行有效控制，是步进电动机高性能控制的重要手段[13-16]。本文以高性能控制芯片SPC1068为基础，设计一款高效稳定的电机转矩控制系统。利用转矩矢量控制方法，在已知所需转矩的情况下，通过控制芯片直接计算获得最优矢量电流，摆脱传统查表电流的获取，提高了电机转矩可控性和实时性，优化了电流控制效率。在步进电动机矢量控制闭环系统中，主控芯片进行转矩计算获得最优矢量电流，经矢量控制和PWM控制对电机施加绕组电压。通过增量式旋转编码器将转子位置实时反馈给控制芯片，实现对电机转矩、电流的闭环控制。仿真实验证明，系统能实现对电机转矩的有效控制，且具有较高的动态稳定性。

1 两相混合式步进电动机转矩矢量控制

转矩矢量控制是对电机定子绕组电流的相位和大小进行控制。将定子两相绕组电流进行坐标变换，得交、直轴电流。通过控制交、直轴电流的相位和大小，实现对电机转矩的有效控制。

对定子绕组电流ia,ib进行坐标变换，可得d,q轴上电流id,iq，如下：

(1)

利用磁共能得电机电磁转矩表达式：

pImMsr(-iasinθ+ibcosθ) (2)

式中：p为电机转子齿个数；Im为永磁体等效励磁电流；L2为电机绕组自感的基波分量；Msr为定转子间等效互感。

将式(1)代入式(2)中可得：

Tm=-2pL2idiq+pImMsriq(3)

取d,q轴电感:

(4)

式中:L0为电机绕组自感的平均分量。将式(4)代入式(2)得到:

Tm=p(Ld-Lq)idiq+pImMsriq(5)

式(5)为两相混合式步进电动机电磁转矩表达式。在已知交、直轴电流时，可得电机电磁转矩值。Tm是由磁阻效应产生的磁阻转矩和主电磁转矩共同作用得到。通过控制定子交、直轴电流大小和相位来对电磁转矩进行控制。

由式(5)可知，在已知电磁转矩的情况下，交、直轴电流组合有多种形式。在转矩达到的同时，如何将电能效率达到最优，是未来电机控制发展的重要方向。

(6)

(7)

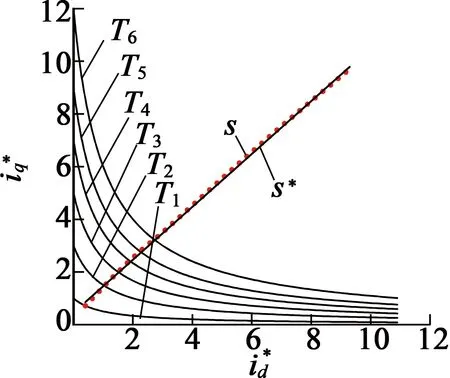
图1恒转矩曲线与最优转矩曲线

将式(7)与式(6)联立，得到所需转矩值的交、直轴最优电流:

(8)

采用最优转矩/电流控制策略时，混合式步进电动机的定子电流需要满足：

图2为细分矢量图。控制电流是非线性的，实时计算出每1 ms的d,q轴电流计算量又过于庞大，不符合目前的现实情况。通过参考细分电流的方法，将每一象限均匀地分成n等份，然后取每一等份中的中间矢量作为d,q轴所在区域标准矢量。

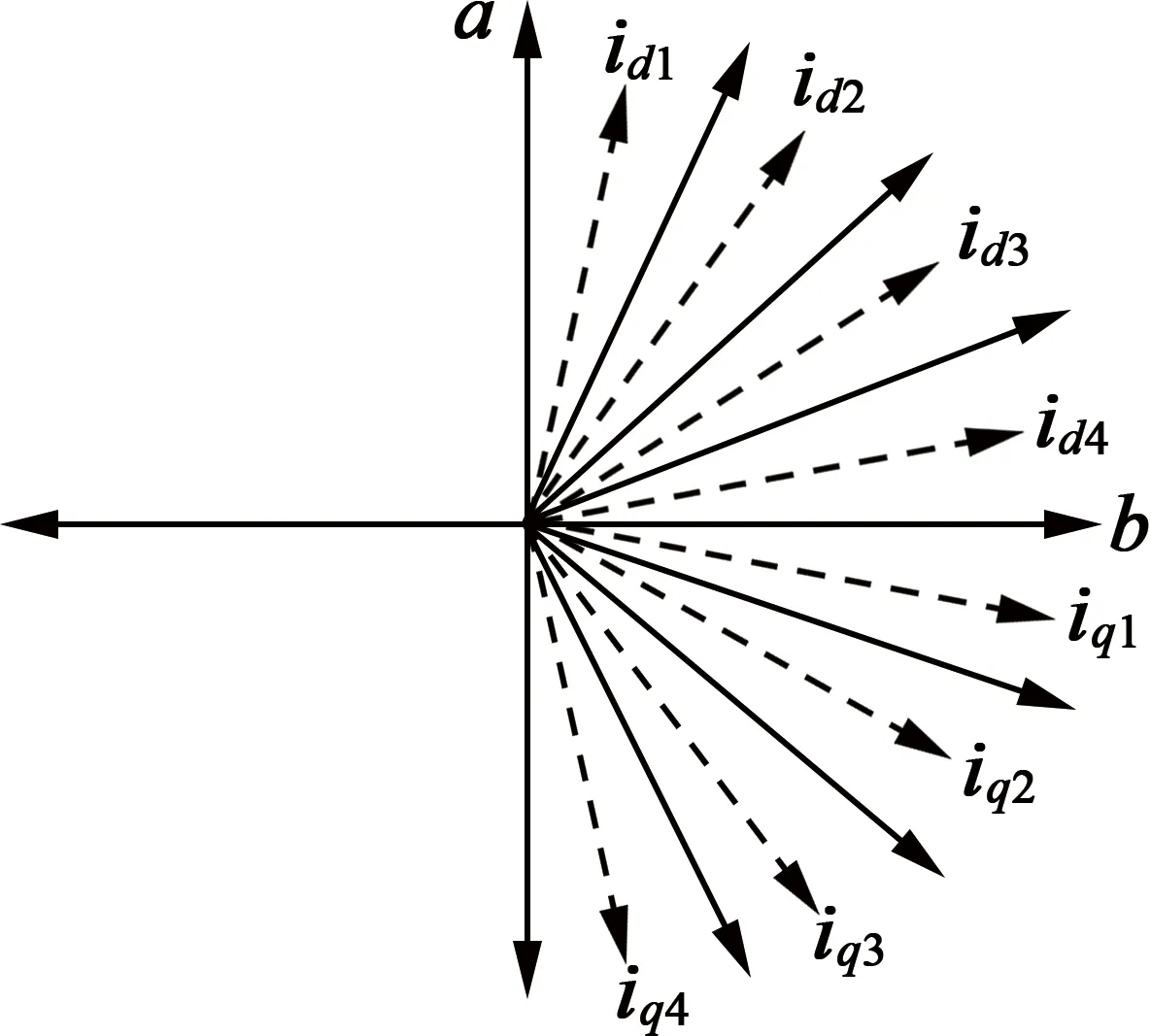
图2细分矢量图

在得到交、直轴电流值以及转子位置角度，通过矢量反变换得到转子绕组电流ia，ib值，如下式：

(10)

增量式旋转编码器可实时、准确地获得电机转子位置角度信息。步进电动机通过矢量细分角度可以有效地控制电机的转矩稳定输出，使步进电动机运行平稳。

2 步进电动机矢量控制的实现

本文使用SPC1068作为主控芯片，它是基于ARM Cortex-M3为内核的32位微控制器，最高支持150 MHz CPU主频和零等待状态。相对于其他的ARM系列的芯片，SPC1068更适合电机产品的开发，14路PWM输出，7组互补PWM。专为电机/电源设计的PWM与ADC连动功能，支持PWM周期内任一时点触发采样 。16通道(16组单端，8组差分输入)，最高4×106Hz采样速率，拥有2个Sample/Hold电路，支持同步瞬间采样。

图3是两相混合式步进电动机可控转矩矢量控制原理图。将所需的电机转矩值输入到SPC1068中，通过式(8)、式(9)，可得交、直轴电流的最优估计值。

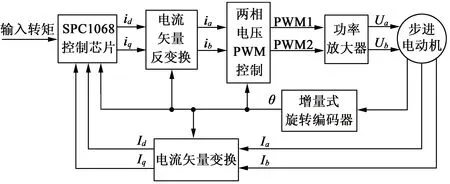
图3步进电动机可控转矩矢量控制系统图

将获得的最优交、直电流进行电流矢量反变换，得电机a,b相绕组电流。对两相电压进行PWM控制，输出脉冲宽度不同的相电压Ua,Ub到电机绕组。增量式旋转编码器能将电机转子位置角度实时、准确地反馈给控制系统。同时电机绕组的反馈电流Ia,Ib，经过矢量变换得到反馈交、直电流Id,Iq，反馈到SPC1068控制器与估计矢量电流进行比较，实现对电机转矩、电流的精确控制和实时监控。

3 仿真实验

在不考虑定子极间与端部中的漏磁、永磁体回路的漏磁、磁滞、涡流以及饱和等情况下，得到两相混合式步进电动机的电压平衡方程：

2L2[iasin(2θ)-ibcos(2θ)]-kmωsinθ(11)

2L2[iasin(2θ)+ibcos(2θ)]+kmωsinθ(12)

式中:km为永磁体内部磁压降系数。

电磁转矩方程：

(13)

由式(11)～式(13)可得电机数学方程的微分形式：

(14)

由式(2)、式(14)，建立两相混合式步进电动机电机数学模型。输入量为电机绕组a，b相电压和负载转矩，输出量为步进电动机绕组电流、电磁转矩、角速度以及角位移。

图4为步进电动机转矩矢量控制系统仿真图，向SPC1068中输入所需转矩，计算得到达到转矩所需要的最优矢量电流值。经过矢量控制和PWM电流控制，获得电机绕组电压，实现对电机的转矩、转速控制。电机将转子角度位置及绕组电流值反馈给控制系统，控制芯片对反馈矢量电流和估计矢量电流进行比较，调节矢量电流的输出。

图4步进电动机转矩矢量控制系统仿真图

进行Simulink仿真实验，模拟电机低频突加速工作状态。初始转矩值设定为7 N·m，2.5 s后将转矩值设定为15 N·m，负载设置为6 N·m。仿真结果如图5～图9所示。

图5电机绕组电流图

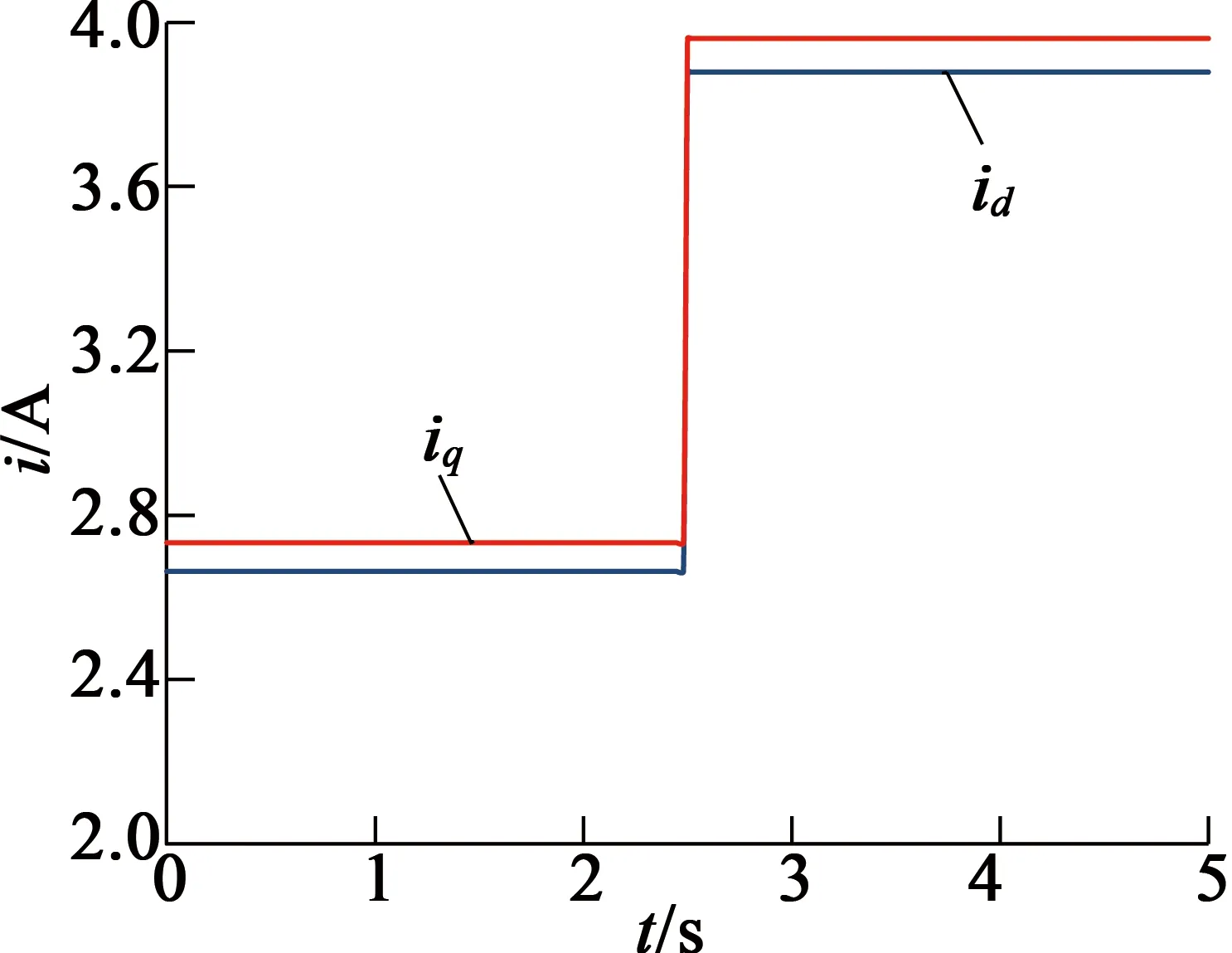
图6交、直电流优化值仿真图

图7电机转矩仿真图

图8电机转速仿真值图

图9电机转子位置仿真图

由图5、图6可看出，电机绕组电流响应稳定，在突加转矩后，系统调节时间短，能迅速达到稳定正弦波状态。控制芯片能准确计算出达到预期转矩的交、直轴电流最优值。由图7可知，电机转矩输出准确，在突加转矩后，系统经过短暂调节，能迅速达到预期输出转矩的稳定状态，保证了电机转矩输出可控的准确度。由图8、图9可知，电机低转速运行平稳，在突加速状态下，转速响应迅速、无振荡过冲。电机转子的位置角度呈线性化，有效改善了电机低频振荡和失步问题。

4 结 语

仿真结果显示，基于高性能SPC1068的可控转矩矢量控制系统下的步进电动机输出转矩响应迅速稳定。通过控制电流实现了对电机转矩的直接控制，有效地解决了电机低频振荡和失步问题。在大范围改变电机输出转矩的工作状况下，电机转矩、转速能在较短的时间内达到预期稳态。通过对转矩的控制，还可以实现电机加速、匀速和减速各种工作状态的控制，并且由SPC1068控制芯片组成的硬件电路结构简单，成本较低，能够满足多种场合下的工作应用要求。