基于扰动补偿的表贴式PMSM滑模电流控制研究

阚卫峰，陈 渠，齐仲安

(1. 上汽集团商用车技术中心，上海 200041； 2. 上海交通大学，上海 200240； 3. 上海申沃客车有限公司，上海 201108)

0 引 言

表贴式永磁同步电机(以下简称SPMSM)具有高效、高功率密度、高可靠性等优点，广泛应用于新能源汽车驱动系统中[1-2]。矢量控制是一种常见的永磁同步电机控制框架[3]。该框架具有两个控制环：外环的速度控制环和内环的电流控制环。由于SPMSM的输出转矩仅正比于q轴电流，因此电流控制环对于转矩控制应用尤其重要。近年来，出现了许多永磁同步电机的电流控制策略[4-8]。文献[4]报道了一个具备鲁棒性能的电流控制器，该控制器可以改善传统电流控制器的鲁棒性和动态响应性能。文献[5]将在线参数自调节的方法引用到PI电流控制器。文献[6]通过使用预测电流控制策略降低了速度波动。文献[7-8]分别使用了电流补偿策略和扰动估计策略来改善电流控制器的性能。

滑模控制(以下简称SMC)策略是一种有效的电机控制方法，该方法可以应用到速度控制器[9-10]，也可以应用到电流控制器[4,11]。SMC策略具有快速响应、对系统参数和扰动不敏感等优点，然而传统SMC策略会导致控制系统出现抖振现象。一些文献使用将开关函数替换为饱和函数或sigmoid函数的方法降低抖振[12-13]。 不过此方法会降低系统的响应速度。另一种解决方案是使用高阶SMC[10,14]。

本文设计了一种基于新的趋近率的SPMSM滑模电流控制策略，并对电机的各种扰动进行了统一的估计和补偿。新的趋近率是基于Super-Twisting策略设计的。新的具备扰动补偿的SPMSM滑模电流控制策略具有快速的响应性能和较低的抖振。最后，通过仿真模型和电机控制系统，验证了该控制策略。

1 永磁同步电机数学模型

SPMSM的模型由电压方程、磁链方程、电磁转矩方程和转子运动方程组成[2]。根据这些方程可以得到表贴式永磁同步电机的误差微分方程组：

(1)

式中：ωm是机械角速度，ωr是电角速度，ωm=ωr/p;id是d轴电流；iq是q轴电流；ud是d轴电压；uq是q轴电压；R是定子电阻；L是绕组电感，L=Ld=Lq；ψf是永磁磁链；p是极对数；Bm是阻尼系数；T是负载转矩；J是运动惯量；ed，eq和em分别是id，iq和ωm的误差；idref，iqref和ωmref分别是id，iq和ωm的参考值。

将参考微分值、阻尼系数、负载转矩和其它扰动统一考虑为综合扰动，式(1)变换：

(2)

式中：δd，δq和δm分别是id，iq和ωm的综合扰动。最后根据式(2)可以获得SPMSM的通用误差方程：

(3)

式中：e表示id，iq或ωm的误差；u表示电压ud或uq；c是一个通用项，对于id，它是Rid/L-iqωr，对于iq，它是Riq/L+idωr+ψfωr/L，对于ωm，它是0；δ表示id，iq或ωm的综合误差。

2 滑模电流控制策略

2.1 矢量控制框架

典型的SPMSM矢量控制结构如图1所示[3]。该结构通过坐标变换对三相电机电流进行了解耦。对SPMSM来说，由于Ld几乎等于Lq，更是可以获得完全的解耦。该框架包含两个控制环，共三个控制器：速度控制器、id控制器和iq控制器。外环是速度控制环，对于转矩控制应用，该环可以取消。内环是电流控制环，主要通过控制iq来调节电机的转速或者转矩。本文主要关注于电流控制器(id控制器和iq控制器)的研究。

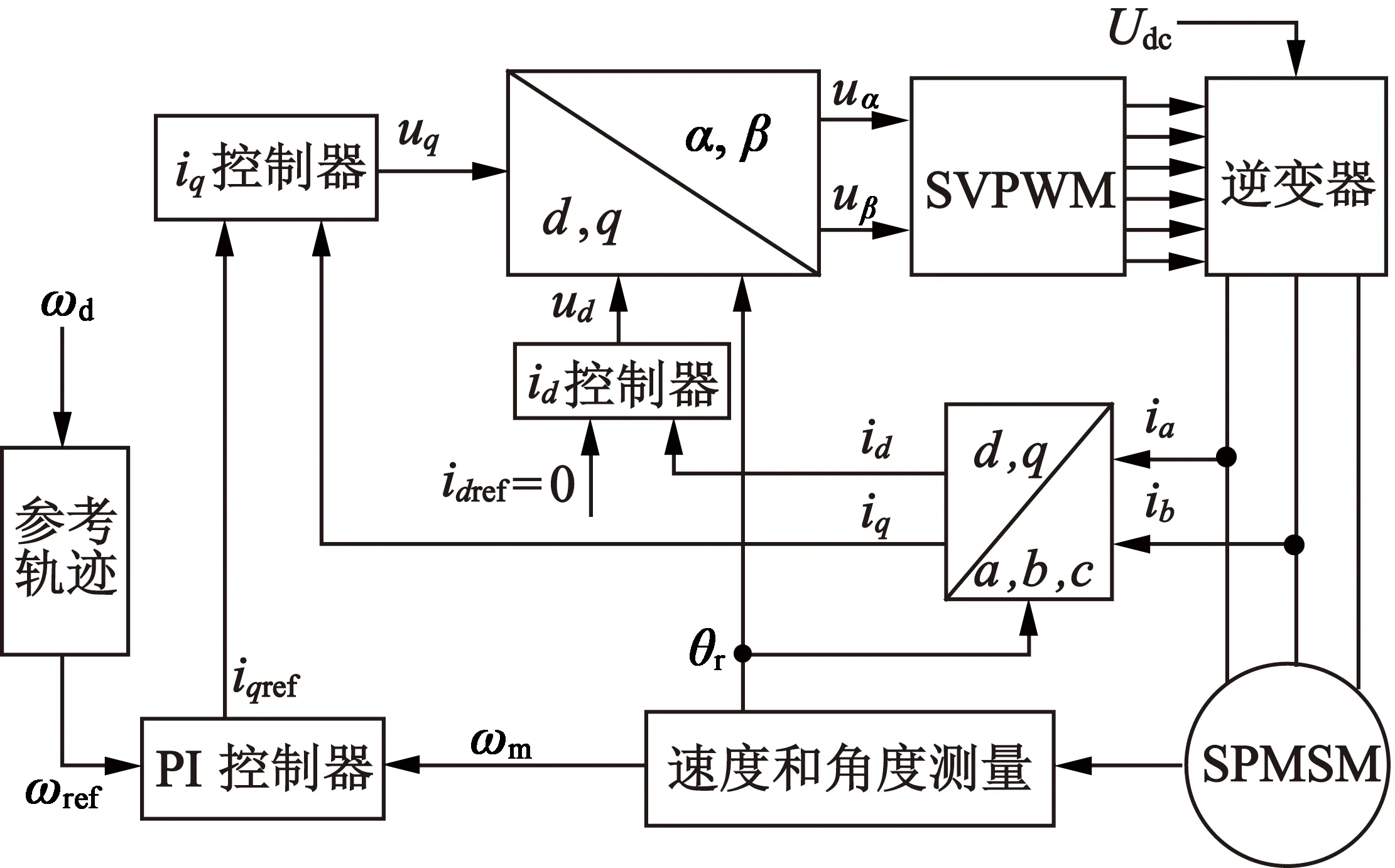
图1 SPMSM 矢量控制框架

2.2 速度控制器

速度控制器使用了一个参考轨迹模块和一个PI控制器，如图2所示。参考轨迹模块用来生成固定斜率的参考速度轨迹，其描述方程：

(4)

式中：ωref是参考速度轨迹；ωd是速度给定值；G是增益；Ts是采样时间；sat是饱和函数；k是计算次数，为正整数。速度控制器的模块图如图2所示。

图2速度控制器

2.3 滑模电流控制器

SMC的设计一般分为两步：选择一个滑模面；设计一个趋近率。基于通用误差方程式(3)，传统滑模电流控制器的滑模面可以选为[15]：

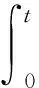
对滑模面求微分，得：

(6)

式中：s是滑模面；α是积分系数；ε是趋近率增益。根据式(3)和式(6)，并忽略扰动，则传统滑模电流控制器的控制律可以表示：

(7)

改进的滑模电流控制器从两个方面进行改进：滑模面和趋近率。对于滑模面的选取，为了提高电流响应速度，使用端末积分滑模面[16]。这样新的端末积分滑模面：

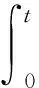
式中：0 <λ< 1。同理，可以得到滑模面的微分：

(9)

v是趋近率，这样新的滑模控制器控制率：

(10)

在式(7)中，v是-sgn(s)。 这种基于简单开关函数的趋近率趋近速度有限，且会造成控制信号中出现高频的开关谐波。为了解决这个问题，本文基于Super-Twisting 趋近策略[17]，提出了一种改进的趋近率：

式中：β，k，φ和χ是趋近率的增益项。

滑模控制器稳定性准则：

(12)

代入趋近率v可得:

ε表示滑模控制器的趋近速度。为了保证系统稳定，ε必须大于0。这样式(13)可以分为两部分。第一部分是:

(14)

可以看到，这部分是稳定的，同时β需要合理的设计。第二部分是：

(15)

因为积分项的存在，这一部分的稳定性是不确定的，因此χ和φ对系统的稳定性是有影响的。SMC中滑模面s是在0附近的,这一部分的值会很小，并接近于0。为了保证系统的稳定性，χ和φ应该取较小的值。

2.4 扰动估计策略

综合扰动δ包含参考微分、阻尼系数、负载转矩和其它扰动。δ存在于控制律式(10)中，会影响控制律的控制性能。扰动估计策略可以提供一个δ的估计值，从而获得更好的控制律。根据式(3)，可以获得综合扰动δ的计算公式:

(16)

在式(13)和式(16)中，均存在微分计算，而一般的微分计算法会带有大量的谐波。因此，这里使用鲁棒微分器和FIR滤波器的串联结构获得一个不带有谐波的微分值。FIR滤波器使用20阶10 kHz。鲁棒微分器的设计方法如下[18]：设定一个输入信号e(t)并假设它的微分绝对值的上限值为X(X>0)，可得:

式中：ees是e的估计值，ees(0) =e(0)；m和d是系数，取值范围如下：

(18)

电流控制器的方框图如图3所示。

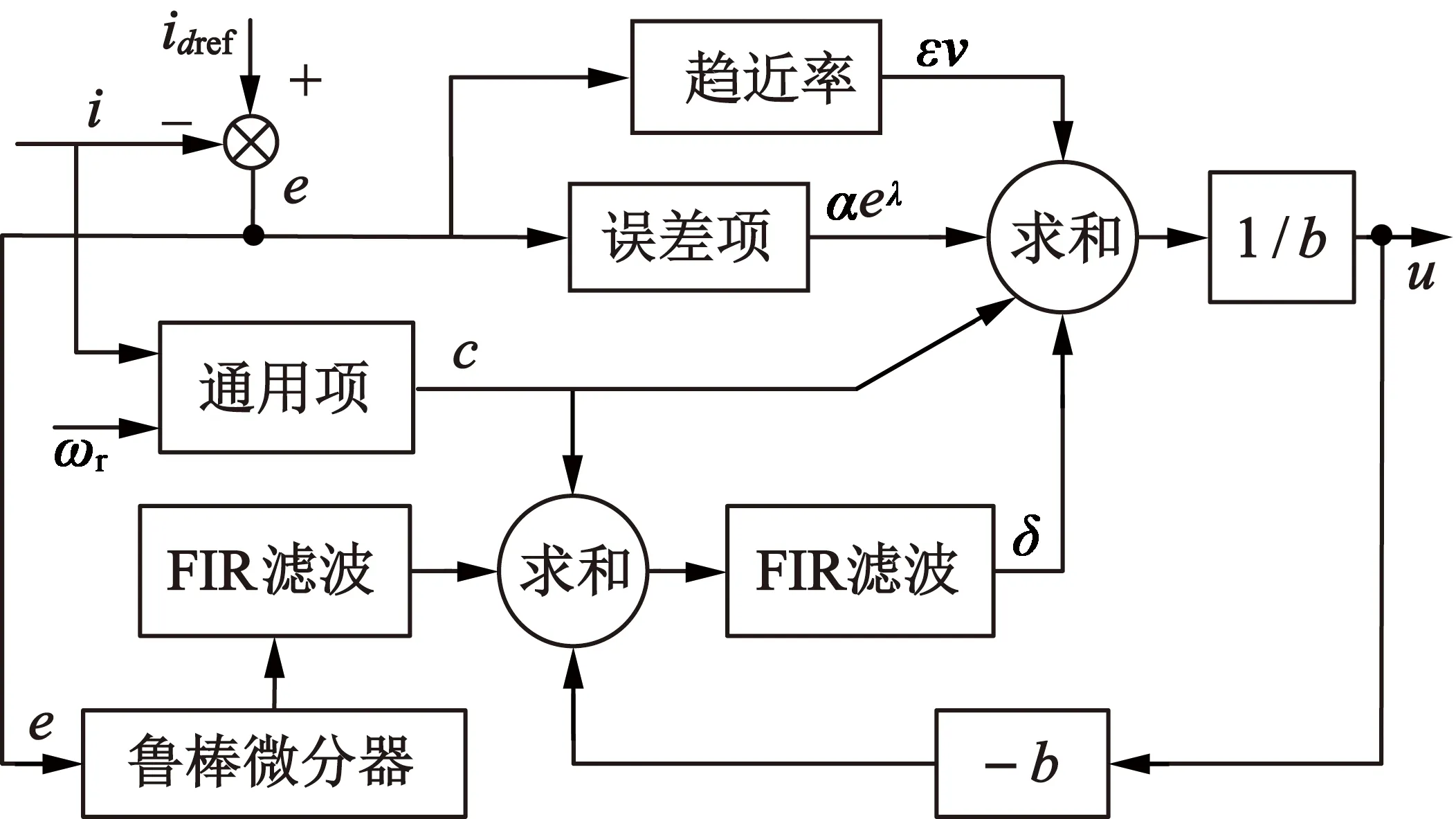
图3 电流控制器

3 仿真验证

为了验证所设计的滑模控制律性能，在MATLAB/Simulink软件中搭建了以上控制策略和SPMSM的仿真模型。SPMSM和相关电路模型使用 SimPowerSystems工具箱搭建，控制策略使用Simulink常用模块搭建。仿真的参数设置如表1所示。

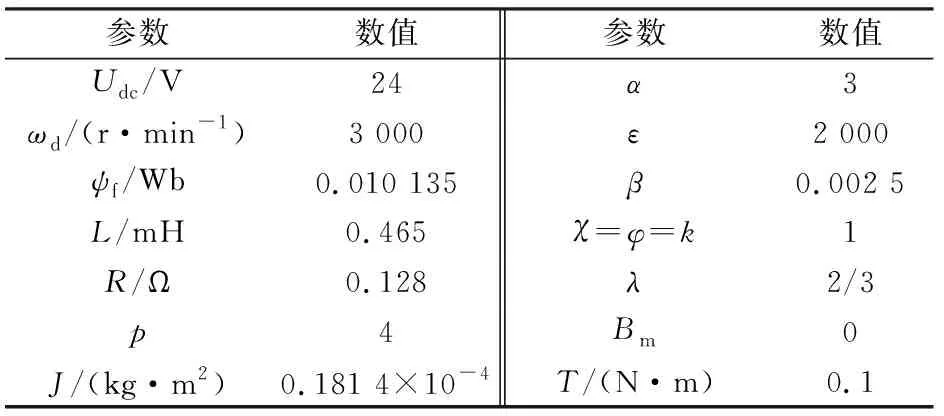
表1 SPMSM仿真参数

3.1 电流控制比较

图4和图5是新的SMC策略和传统SMC策略在表1参数下电机起动过程中的q轴电流iq的响应曲线。传统滑模与新的滑模使用相同的速度控制器和相同的参数(α和ε)。从图4可以看到，传统SMC策略具有更大的电流纹波，而新的SMC策略幅值电流纹波更小，谐波更低。从图5可以看到,新的SMC策略具有更快的响应速度，更小的超调量，对于参考电流的追踪更加精确。

(a) 传统SMC

(b) 新的SMC

图4iq波形比较

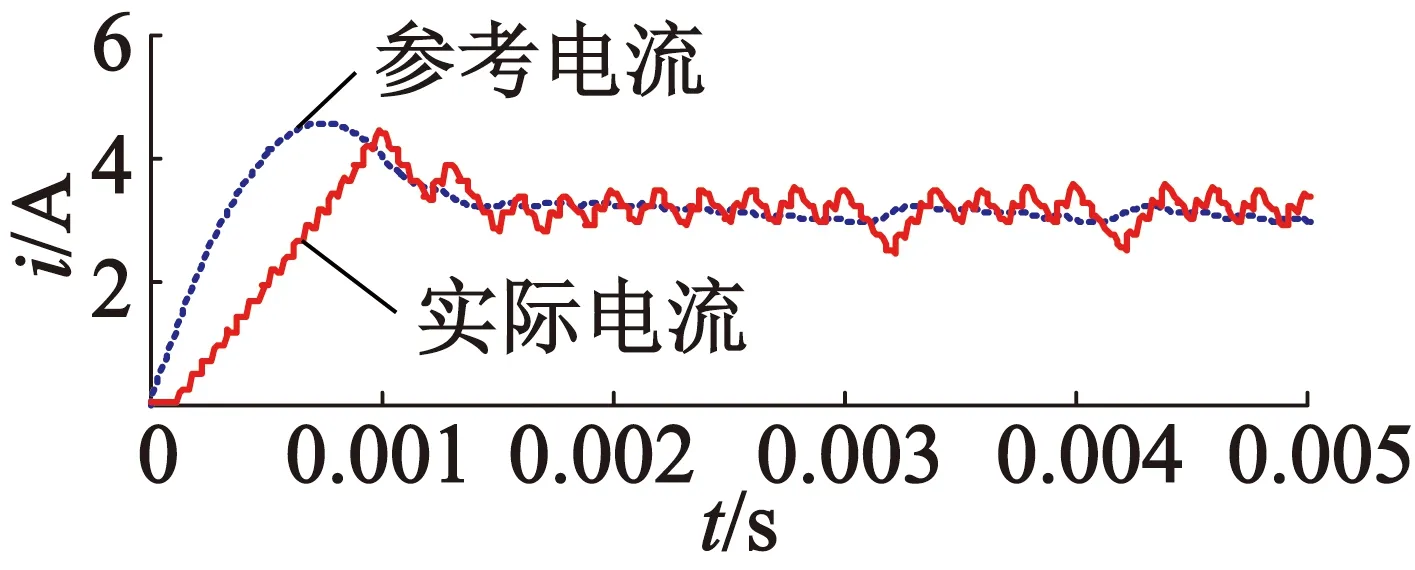
(a) 传统SMC

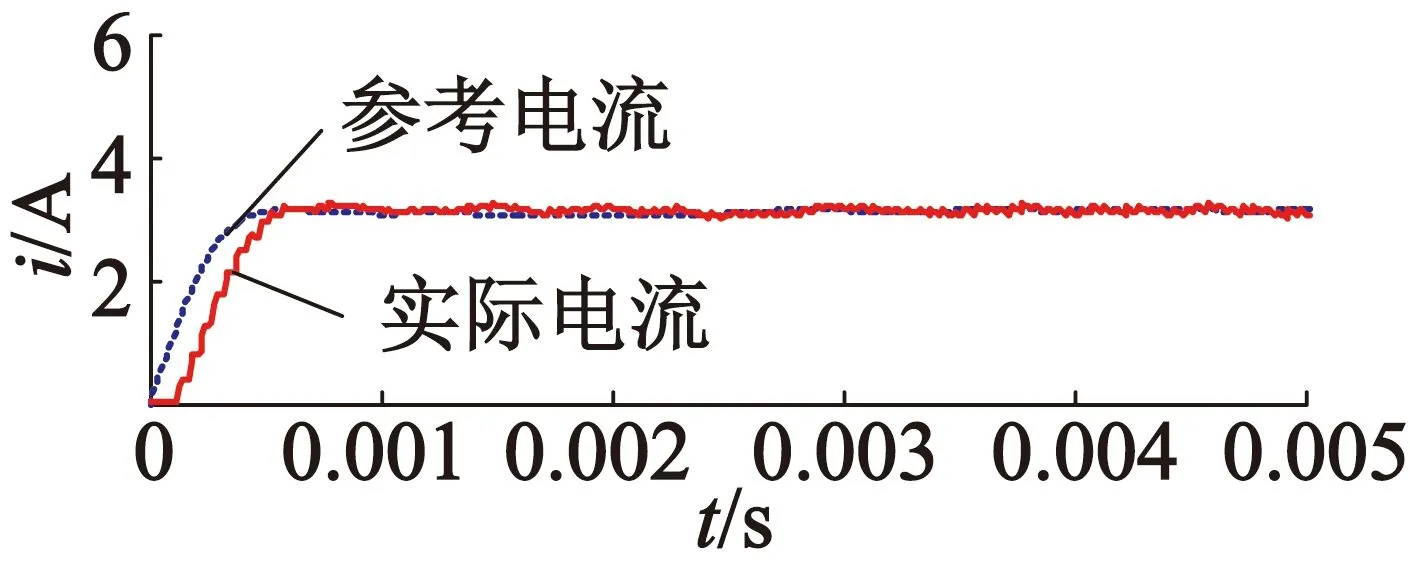
(b) 新的SMC

图5电动起动时iq响应

3.2 性能测试

图6为变转矩测试时的iq响应结果。性能测试的环境：转速ωd恒定为3 000 r/min；负载转矩T的初始值为0.1 N·m，之后在0.2 s时变为0.2 N·m，最后在0.4 s时变回0.1 N·m。从图6的响应结果可以看到，实际电流可以精确地追踪参考电流的变化。在整个控制范围内，电流响应精确、稳定。由于在SPMSM中电磁转矩和iq线性正相关，因此，从图4～图6的结果中可知，新的SMC策略具有较快的转矩响应速度，精确的转矩追踪效果。适合于SPMSM的转矩控制应用或转速控制中的电流环控制应用。

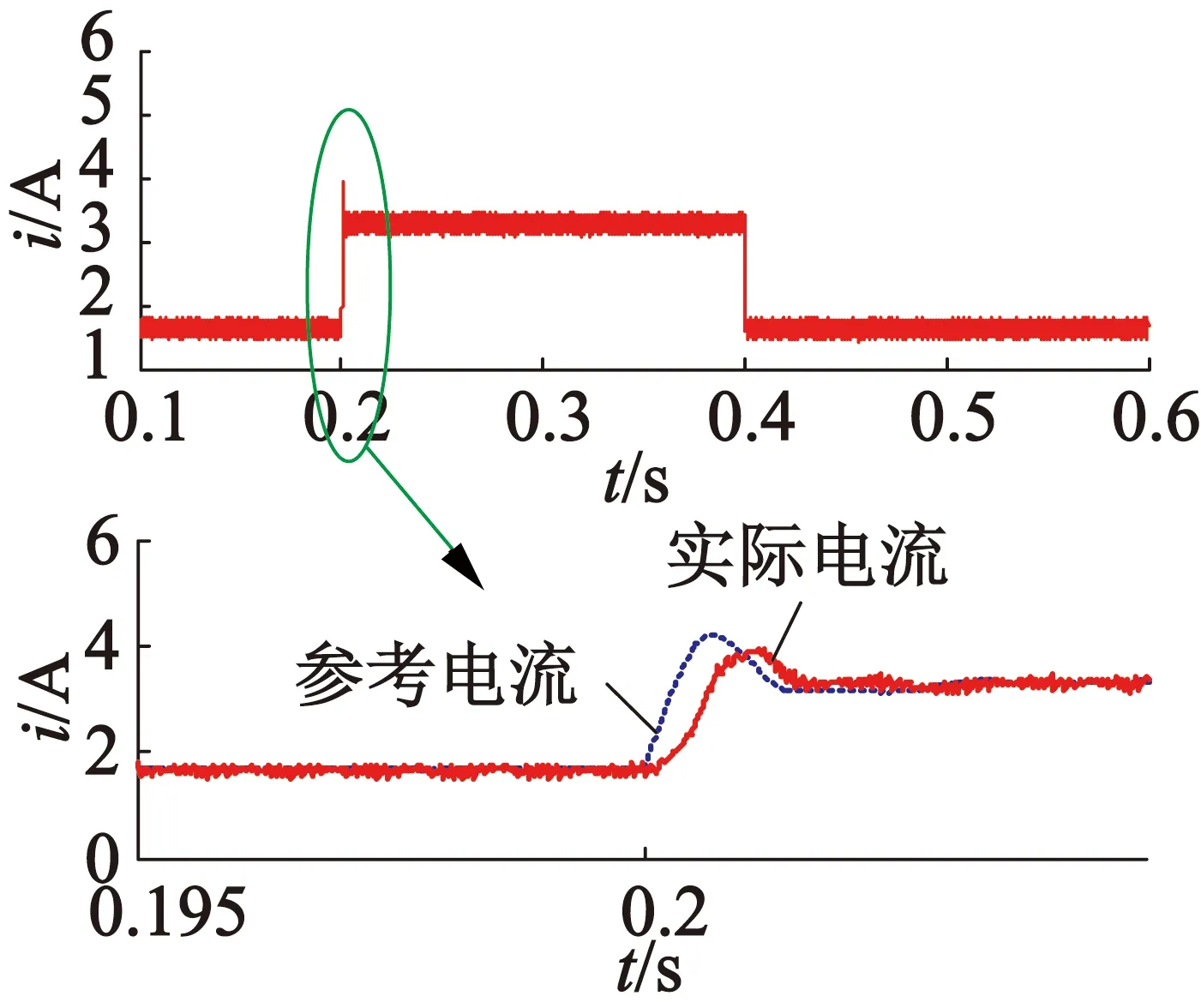
图6 变转矩下的iq响应

4 实验验证

为了进一步验证该策略的可行性，利用一个SPMSM控制系统进行了电机控制实验。电机的参数如表1所示，控制参数和负载情况根据实际情况进行了一定的调整，由于控制器运算能力限制，实验中未包含扰动估计算法。实验配置如图7所示。实验中使用UART串口发送和采集电机数据，使用MATLAB对数据进行处理和绘图。

图7 实验配置

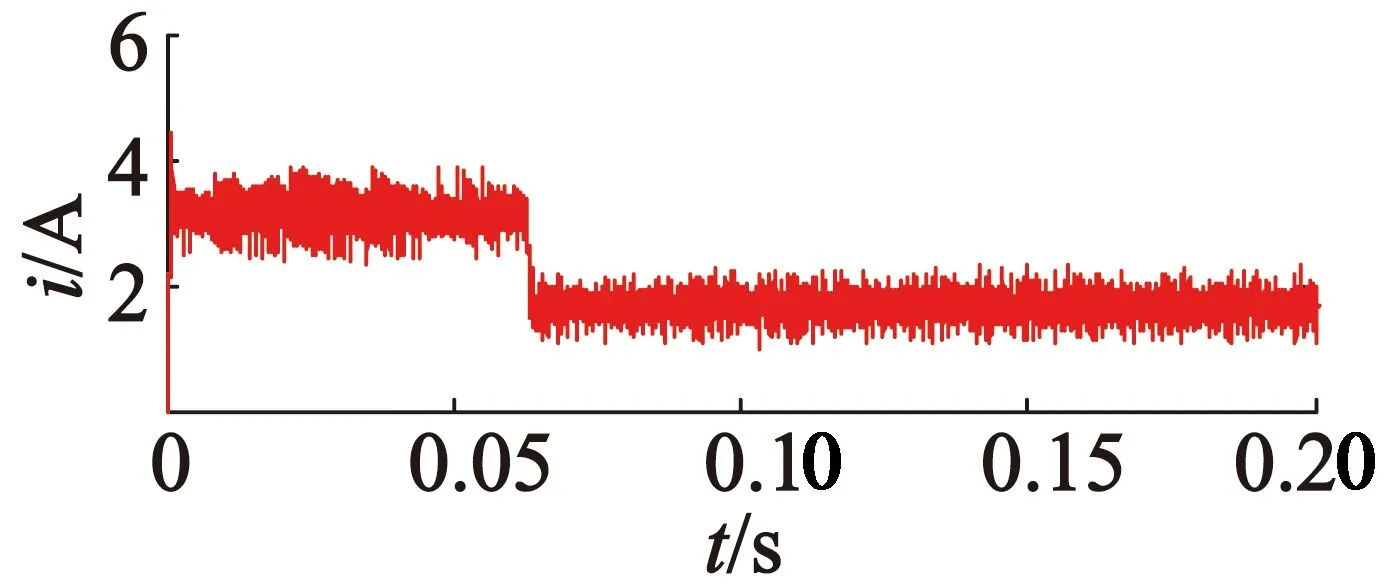
图8和图9为实验结果。其中图8为转速实验结果，图9为电流实验结果。电流和转速的实际值可以较好地跟踪参考值的变化。可以看到，所提出的控制策略是可行和有效的。

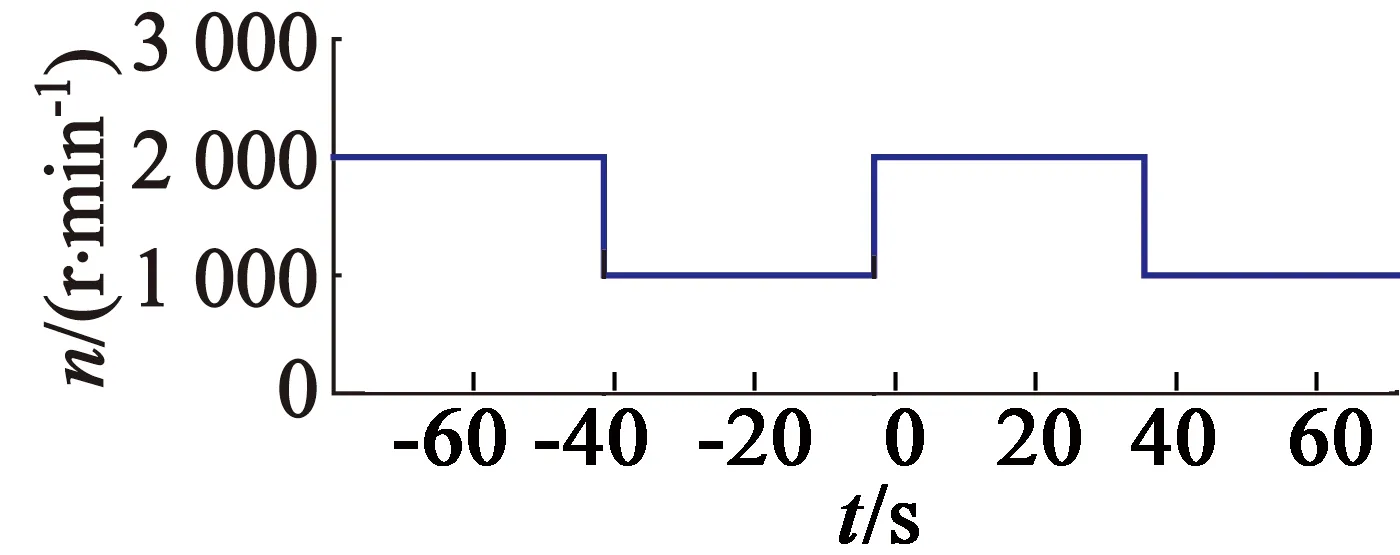
(a) 参考速度

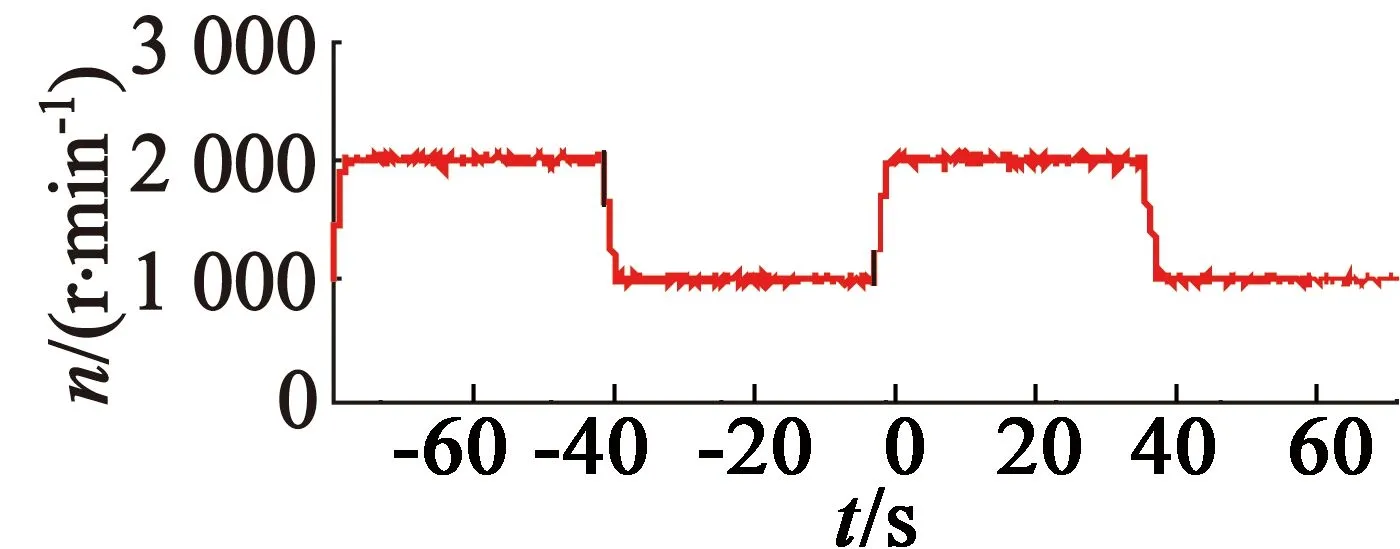
(b) 实际速度

图8转速响应实验结果

(a) q轴电流参考

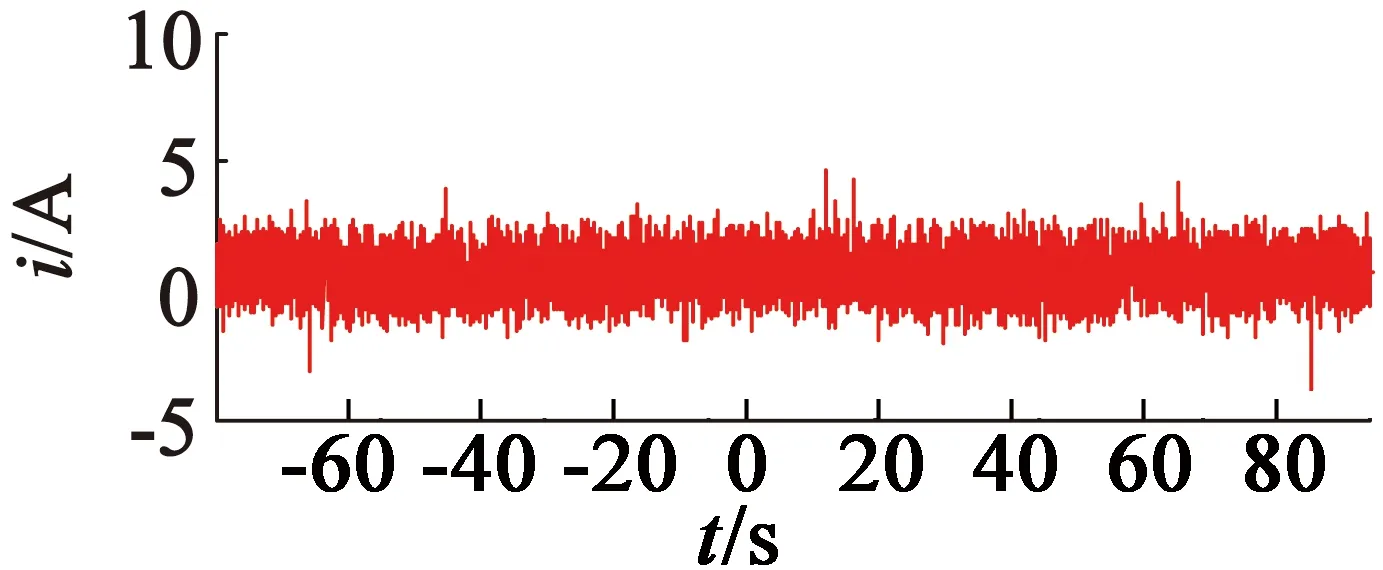
(b)q轴电流测量值

图9iq响应实验结果

5 结 语

针对SPMSM，设计了一种具有扰动补偿能力的滑模电流控制策略。该控制策略能够有效改善滑模控制中出现的抖振现象，提高电流响应速度和追踪精度。最后通过MATLAB/Simulink仿真模型和电机实验系统进行了仿真和实验研究。结果表明，相比于传统的SMC策略，在新的控制策略下，电流响应速度和精度明显提高，电流稳定谐波大为减小。新的电流控制策略可靠、有效。