考虑过街行人影响的右转车辆间隙接受模型

王姝淇， 魏丽英

(北京交通大学交通运输学院，北京 100044)

在城市道路交通系统中，道路交叉口是主要的行人事故发生地。据调查，80%的行人事故发生在交叉口[1]。在信号控制交叉口，行人也会与转弯机动车发生冲突，甚至发生事故。《中华人民共和国道路交通安全法》第四十七条明确规定“机动车行经人行横道时，应当减速行驶；遇行人正在通过人行横道，应当停车让行。”[2]但实际生活中，机动车和行人的通行多如博弈，各自寻找可穿越间隙通过，争夺道路使用权。司机冒风险接受较小的时间间隙，很可能与行人产生冲突，甚至发生事故，造成交通延误，带来安全风险。

目前国内外对穿越间隙的研究多为对机动车之间穿越间隙或行人对机动车间隙接受行为的研究。国外学者对机动车的临界间隙的研究已经提出了很多方法，如：Raff法[3]、Ashworth的方法[4]、极大似然估计法[5]、Hewitt法[6]、Clearing behavior法[7]等。同时，对人车穿越间隙的影响因素也进行了许多分析。如Onelcin等[8]对土耳其6个交叉路口的行人违章过街行为进行了调查，发现车速对安全边际、穿越时间、距离间隙有较大影响，人群数对穿越时间有影响。行人是否穿越取决于距离间隙而不是时间间隙。Pawar等[9]对印度路段行人过街建立了6个二元logit模型，分析了时间和距离对接受间隙的影响，发现冲突车辆速度对距离间隙有较大影响，对时间间隙无影响。潘丽等[10]分析了行人、自行车、电动自行车违章时接受间隙和拒绝间隙的大小及其影响因素，使用生存分析法对违规者间隙接受行为建模，得出不同交通方式间隙的分布没有显著差异的结论。Maurya等[11]分析了司机性别、年龄、是否有乘客、来车速度、等待时间、冲突车辆大小、拒绝间隙次数对摩托车、三轮车和小汽车的影响程度。

目前对转弯机动车穿越过街行人的间隙接受行为的研究相对较少。Asano等[12]发现左转车辆路径的变化与其下游人行横道处和行人的冲突点分布有关。Schroeder等[13]使用多种logit模型研究了车辆对行人的让行行为，发现驾驶员更可能让行于速度较快的行人，车辆在车队中或速度较大时让行率减小。李珊珊[14]分析了右转车辆与行人间的干扰机理，建立了右转机动车、自行车和行人的相互干扰模型。Alhajyaseen[15]对信号交叉口车辆左转时驾驶员对行人的可接受间隙进行了研究，发现行人的移动方向对司机间隙有影响，并用威布尔分布函数建立了间隙的概率接受模型，同时发现车辆离开速度受过马路行人数量影响。

本文采用Wu等[16]的方法，基于宏观概率平衡估计交叉口右转司机的临界间隙，借鉴人车间隙和车车间隙的研究经验和方法，对右转车辆的间隙接受行为进行进一步地研究。

1 数据收集与处理

本文选取辽宁省营口市渤海大街与市府路交叉口和北京市丹棱街与中关村大街交叉口作为调研地点。调查方式采用高点拍摄。

第一个交叉口附近商场较多，选取人流量较大的周六上午10:00—12:00进行拍摄，该交叉口为十字形交叉口，信号灯为四相位，周期为153 s。

第二个交叉口选取周二上午8:00—10:00早高峰进行拍摄，该交叉口为丁字形交叉口，信号灯为两相位，周期为125 s。

本文使用Adobe Premiere软件进行视频的播放及数据的析取，时间精确到0.04 s。通过视频观测，分别对右转机动车和行人计数，计算小时交通量，结果如表1所示。其中丹棱街-中关村大街交叉口有较大的行人流量，交叉口各方向车流量相差不大。

表1 调查点平均右转车辆需求及行人需求

间隙分为两种类型。第一种类型为时间滞后(lag)，是行人到达冲突区域的时间。第二种类型为时间间隔(gap)，是两个连续行人的时间差，即第一个行人离开冲突区域至第二个行人到达冲突区域的时间间隔。

本文的冲突区域定义为车辆自身宽度范围与人行横道交集的区域。计算间隙时，不包括行人在冲突区域内的时间。车辆到达人行横道处时，若行人位于冲突区域中，则为冲突，不算作间隙。

根据行人的运动方向，可将间隙细分为以下五类：类型A为行人从车辆近端过街；类型B为行人从车辆远端过街；类型C为车辆在多个近端行人间穿越；类型D为车辆在多个远端行人间穿越；类型E为多个行人从车辆两侧同时过街。lag包括A、B两种类型，gap包括C、D、E三种类型。其中，近端行人指靠近车辆一侧的行人，远端行人是指远离车辆一侧的行人，如图1所示。

图1 间隙分类图Fig.1 Lags/gaps classification chart

司机决定是否接受间隙的行为可能发生在到达停车线至通过人行横道的全部转向过程中，受过街行人的速度及移动方向、车辆速度的影响，有随机性。不同司机接受间隙的可能性也不同，没有一致性。本文假设司机决定是否接受间隙的时刻为车头刚到达人行横道时或停车后重新启动时。

利用式(1)计算5种间隙的间隙接受可能性P(X)i,j，所得间隙接受概率分布图如图2所示。

(1)

其中，j为间隙类型A—E；i为间隙时间；Nai,j为类型为j的间隙在时间i的接受间隙的观测数量；Nri,j为类型为j的间隙在时间i的拒绝间隙的观测数量。

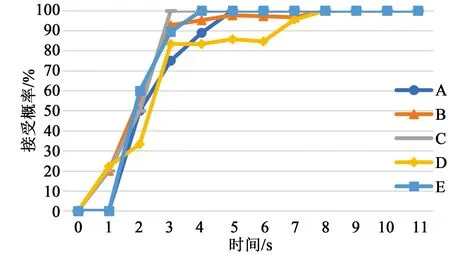
图2 5种间隙接受概率分布图Fig.2 Five kinds of gaps/lags acceptance probabilities distributions

如图3所示,5种类型间隙的接受概率均可通过最小二乘法拟合为累积威布尔分布。利用威布尔函数进行建模，可以分析交叉口几何布局、交通条件等因素对参数α和β是如何影响的，以便应用于仿真中[17]。

图3 E型间隙威布尔分布拟合图Fig.3 Fitted cumulative Weibull distribution for E-type gap

本次调研的间隙接受可能性相较于前人调研的可能性相对较大，在3 ～7 s内即达到80%～100%，即司机偏向采取较为激进的策略，愿意接受较短的行人间隙。这可能是受两方面因素影响，首先，大多数司机都接受“滚动间隙”，即会根据人行横道上行人间隙情况逐步向前移动直至穿过人行横道，使司机能接受较小的行人间隙；其次，经过较长时间停车等待的司机，耐心降低，会接受更小的时间间隙。

2 临界间隙

2.1 临界间隙的计算

临界间隙是指行人流允许右转司机安全穿越的最小间隙，随着驾驶员、时间、地点的变化会发生变化。目前，国内外对于机动车之间临界间隙的研究方法有很多种，其中Wu的[16]方法不需提前定义临界间隙的分布函数及假设司机、行人的一致性，计算简单，鲁棒性好，可用于分析司机对行人的临界间隙。因此，本文采用该方法计算行人影响下右转司机的临界间隙。

假设接受间隙的概率分布函数为Fa(t)，拒绝间隙的概率分布函数为Fr(t)，则间隙为t时接受的概率即为1-Fa(t)，不接受的概率为Fa(t)；间隙为t时拒绝的概率为Fr(t)，不拒绝的概率为1-Fr(t)。用Pr,tc(t)表示行人间隙为t时拒绝的概率，Pa,tc(t)表示接受的概率。间隙t如果被拒绝，既可能是服从拒绝间隙分布被拒绝，也可能是服从接受间隙分布未被接受；被接受的情况类似。由此可得概率平衡方程为：

(2)

将式(2)转换为矩阵形式：

(3)

假设临界间隙的概率分布函数为Ftc(t)，则Pr,tc(t)=Ftc(t)，Pa,tc(t)=1-Ftc(t)，代入式(3)可得：

(4)

求解式(4)可得临界间隙的概率分布函数为：

(5)

根据调研数据，接受间隙、拒绝间隙、计算的临界间隙的概率分布函数Fa(t)、Fr(t)、Ftc(t)关系如图4所示，临界间隙的概率分布位于接受间隙和拒绝间隙之间。

根据式(5)，取全部的拒绝间隙，通过Excel来计算临界间隙，求得本次调研司机右转的临界间隙为3.79 s，标准差为4.11。

图4 接受间隙、拒绝间隙、计算的临界间隙的概率分布函数的关系图Fig.4 Relationship diagram of the probability distribution functions for the accepted gaps, the rejected gaps, and the calculated critical gaps

2.2 临界间隙的拟合函数

探究人车临界间隙分布时，多用对数正态分布和威布尔分布对其经验分布进行拟合。

若间隙t服从对数正态分布，即t～N(μ,σ2)，其概率密度函数为：

(6)

威布尔分布的概率分布函数为：

(7)

其中，α,β分别为威布尔分布的比例参数和形状参数。

本文使用MATLAB，对上述估计的临界间隙经验分布模型进行非线性回归分析，将其拟合为对数正态分布和威布尔分布，验证车人临界间隙的分布形式。拟合函数求得临界间隙平均值及其标准差如表2所示，拟合函数如图5和图6所示。

表2 车人临界间隙回归分析结果

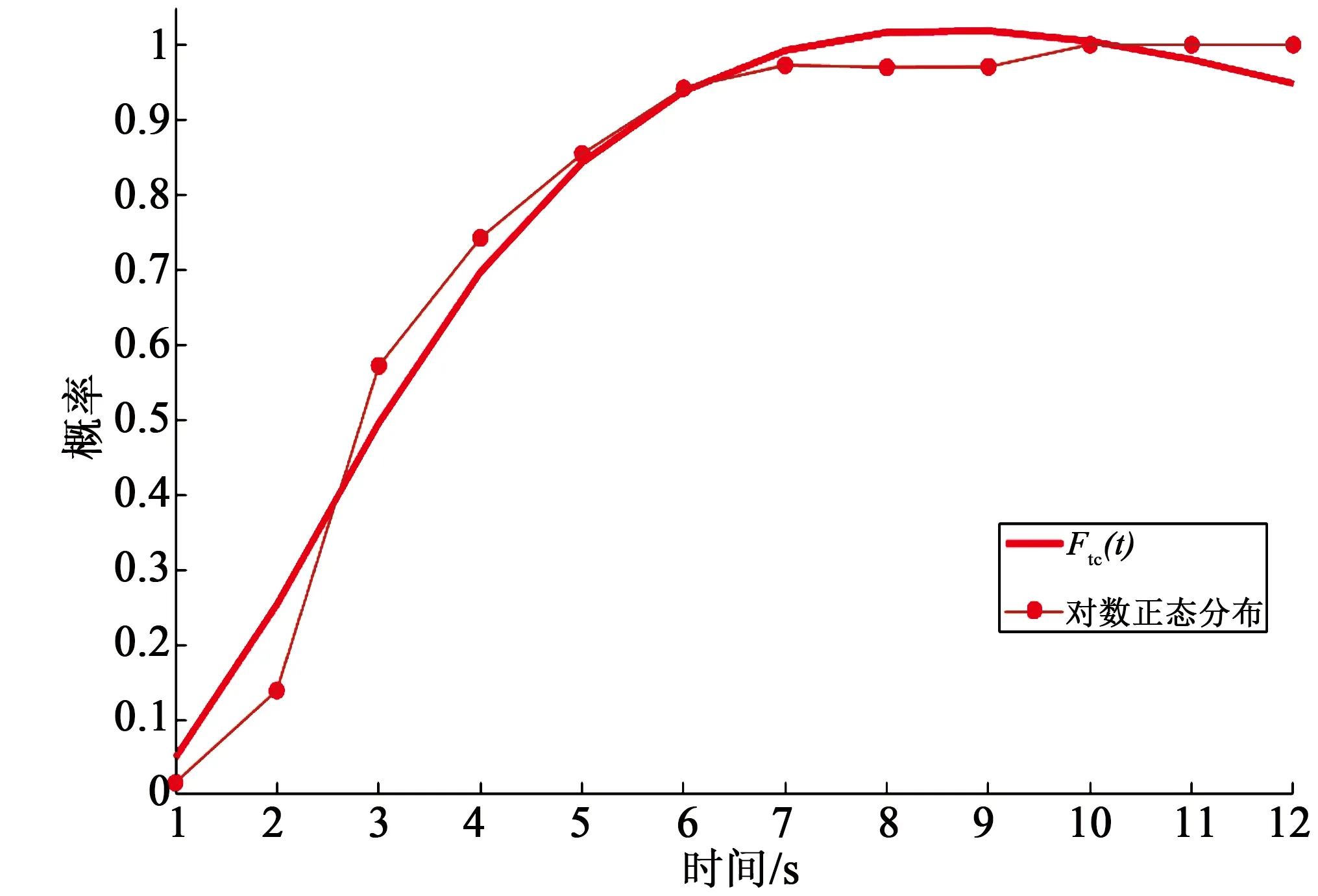
图5 对数正态分布拟合图Fig.5 Fitted Log-normal distributions

图6 威布尔分布拟合图Fig.6 Fitted cumulative Weibull distributions

求得对数正态分布参数μ=2.915 2，σ=0.874 4，其表达式为：

(8)

求得威布尔分布参数α=3.547 5，β=2.437，其表达式为：

(9)

从图5、图6和表2可以看出，威布尔分布求得临界间隙更接近经验分布，且可以更好地平滑经验分布的函数曲线。此外，威布尔函数可以根据参数值的不同呈现多种分布表现形式，如二项分布、正态分布等，可建立多种行为模型，便于使用。综上所述，右转车辆的临界间隙服从威布尔分布。

3 间隙接受模型及影响分析

3.1 建立间隙接受模型

司机右转时对行人间隙接受的行为可能受多种因素的影响，如行人数量、间隙类型等，本章拟用二项logistic回归模型探讨右转司机间隙接受行为的影响因素。

司机对间隙的选择有“拒绝”和“接受”两种方式，用0表示“拒绝”，用1表示“接受”，“是否接受”即作为因变量，来建立logistic回归模型[18]。

设被解释变量y为0/1的二分类变量，有k个元素x1，x2,…,xk影响y=1的取值，则

(10)

其中，P为被解释变量取值为1的概率；xi为解释变量；β0为常数项；βi为各协变量对应的系数值。

将P转换为Ω：

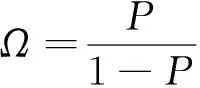
(11)

其中，Ω称为相对风险，是事件发生概率与不发生概率之比。

将Ω转换为lnΩ：

(12)

其中，lnΩ称为LogitP。

经过上述Logit变换，可利用一般线性回归模型建立被解释变量与解释变量之间的多元分析模型，得Logistic回归方程为：

(13)

变换得：

(14)

本文的被解释变量为“是否接受”，解释变量为“间隙类型”、“车型”、“人数”、“间隙大小”、“近端/远端”、“行人流量”，具体的变量说明如表3所示。

表3 协变量说明

“车型”中大型车包括面包车、小货车、公交车、旅游车，由于4种车型相对出租车和私家车比例较小合为大型车。

根据表3中列出的协变量，运用SPSS建立二项logistic模型，结果如表4所示。

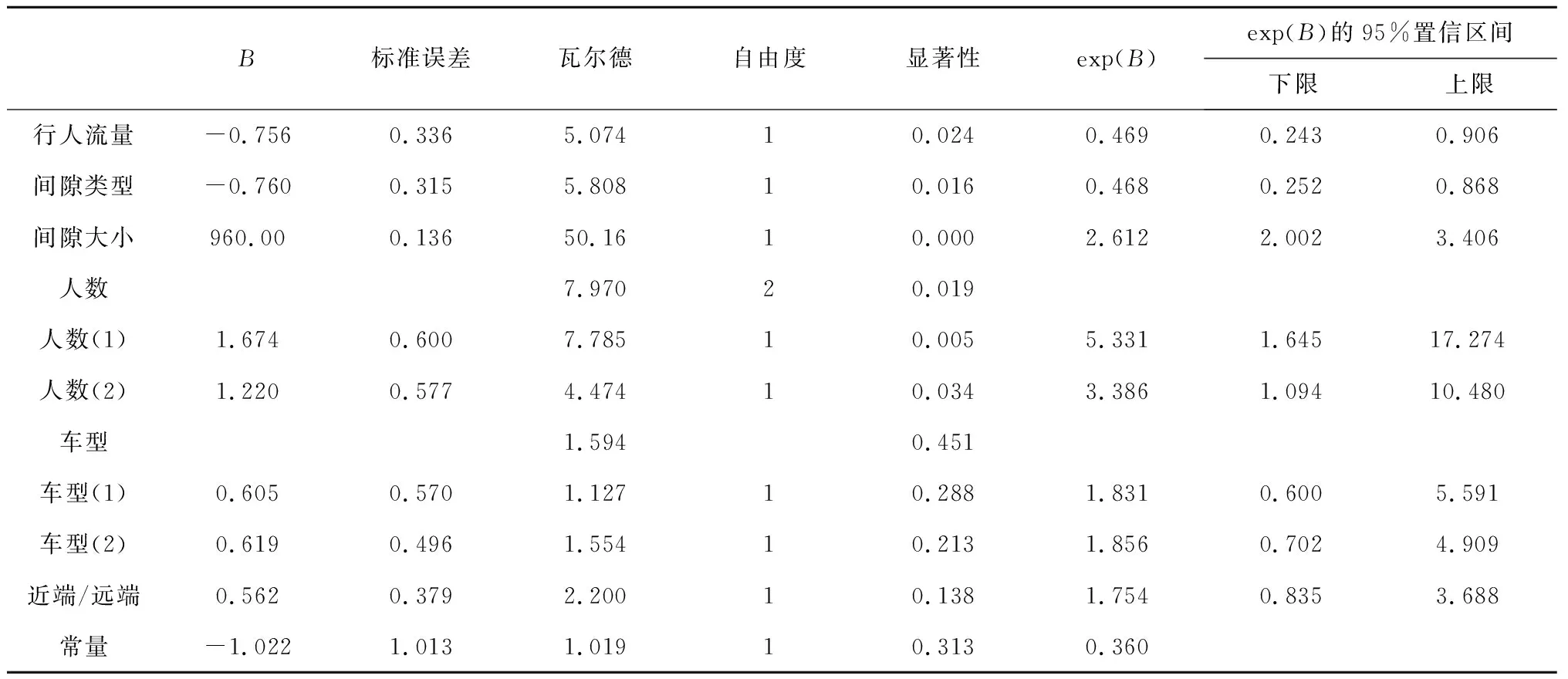
表4 logistic模型协变量估计结果

其中，exp(B)为相对风险比，表示当其他解释变量保持不变时，解释变量xi每增加一个单位所导致的相对风险是原来相对风险的exp(βi)倍。

从表4中可以看出，冲突车型、行人位于近端/远端的显著性水平均大于0.05，表明这两种变量对司机间隙接受行为无显著影响。去除车型、近端/远端两个无关变量，重新进行建模，结果如表5所示。

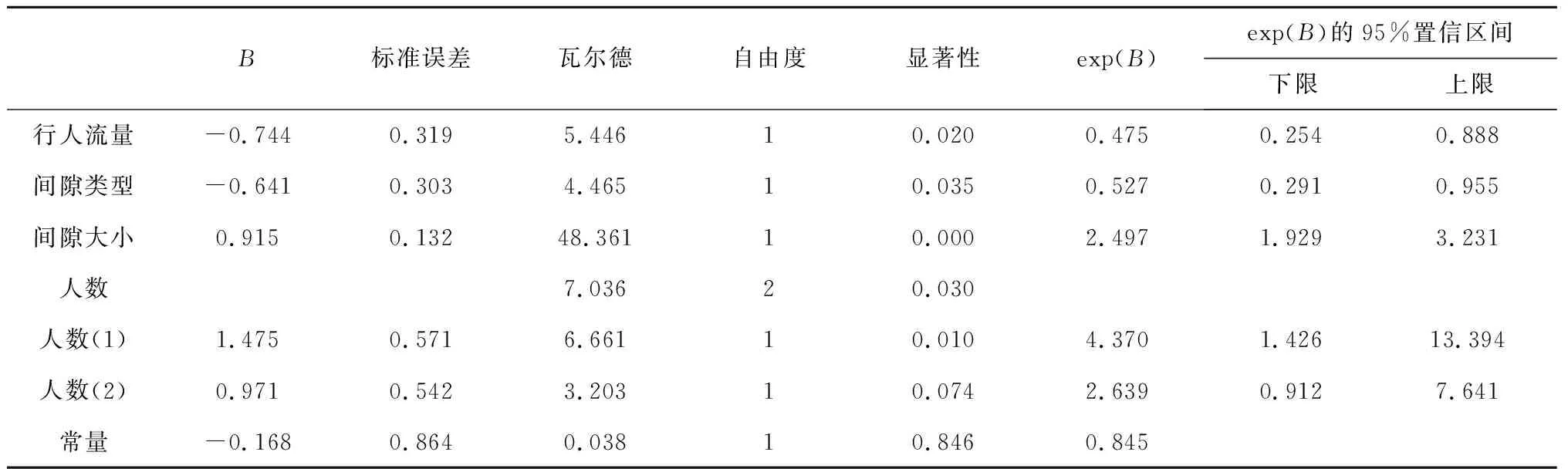
表5 logistic模型协变量估计结果

建立右转司机的间隙接受模型，回归方程为：

LogitP=-0.168-0.744Q-0.641G+0.915L+0.01N(1)

(15)

该模型的-2倍对数似然值相对较低，Cox & SnellR2为0.177，NagelkerkeR2为0.336，混合矩阵模型总体正确率为91.3%，模型拟合优度相对理想。

3.2 各协变量对间隙接受行为的影响分析

根据表5中数据对每个解释变量的影响进行分析。

间隙类型的显著性水平为0.035，其系数值为-0.641，说明间隙类型对间隙接受行为有显著的负影响。因为参照水平为1(lag)，因此表明gap较lag使LogitP平均减少0.641个单位，结合发生比，gap的发生比是lag的0.527倍，司机对较短的gap比较谨慎，更倾向于接受较短的lag。

间隙大小的显著性水平为0，其系数值为0.915，说明间隙大小对间隙接受行为有显著的正影响，间隙值越大，其接受间隙的可能性越大。

行人流量的显著性水平为0.020，其系数值为-0.744，说明行人流量对间隙接受行为有显著的负影响。因为参照水平为1(低)，因此表明高流量较低流量使LogitP平均减少0.744个单位，结合发生比，高流量的发生比是低流量的0.475倍，当行人流量较低时更倾向于接受间隙。

人数的显著性水平为0.030，其中人数(1)的显著性水平为0.010，表明司机对单人过街与人群过街的间隙接受行为有所区别。单人过街的发生比是形成人群(即8人以上)的4.37倍，可见行人为个体时司机更倾向于接受间隙。人数(2)的显著性为0.074，表明当过街行人为多人时，行人数量继续增加对司机的间隙接受行为也不会有显著性影响。

当行人需求较大时，过街行人多会聚集成人群，与机动车相遇时，人群中可能有等待较长时间行人，与司机抢行的可能性增加，司机需减速避让。且人多而分散，交通环境较为复杂，司机的注意力会更为集中，对较小间隙接受的可能性减小，停车让行以避免发生碰撞的可能性增大。当行人需求较小时，过马路行人多为个体，行人多会避让车辆，减速慢行至冲突区域，所以司机接受较小间隙的可能性增加。因此，对行人需求较小的交叉口，更应该加大对其安全的关注。

综上所述，影响司机间隙接受行为的因素为间隙大小、间隙类型、行人流量以及人群数。间隙值较大，行人流量较低时，司机接受间隙的可能性较大；司机对单人过街的间隙接受的可能性更大；司机对较短的gap比较谨慎，更倾向于接受较短的lag。而车型、行人的移动方向(所处近端或远端位置)均对司机间隙接受行为无显著影响。

4 结论

本文通过实证调研，运用统计分析方法对信号交叉口右转车辆对过街行人的间隙接受行为进行了研究。文中对Wu求解临界间隙的方法进行分析，发现该方法也可用于求解右转车辆对过街行人间隙的接受行为，并运用该方法求得调研司机右转的临界间隙为3.79 s。对间隙分布进行拟合，发现右转车辆的接受间隙和临界间隙均服从威布尔分布。同时，运用二项logistic回归建立了右转司机的间隙接受模型，分析其影响因素。结果表明，间隙值较大，行人流量较低时，司机接受间隙的可能性较大；司机对单人过街的间隙接受的可能性更大；司机对较短的gap比较谨慎，更倾向于接受较短的lag。车型、行人的移动方向对司机间隙接受行为无显著影响。此外，调研发现部分司机接受“滚动间隙”，会根据人行横道上行人间隙情况逐步向前移动直至穿过人行横道，使司机能接受较小的行人间隙。

本次研究还存在着一定的局限性，日后可加大样本数据，并对车辆离开速度、交叉口几何特性等因素的影响进行进一步地研究。