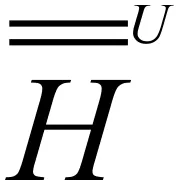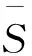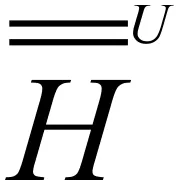强U--富足半群上的同余
2019-02-23韩雪梅李刚
山东科学 2019年1期
韩雪梅, 李刚
(山东师范大学数学与统计学院,山东 济南 250014)
1 引言及预备知识
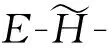
令S为半群,E(S)是S的幂等元集合且U⊆E(S),S上的格林关系为
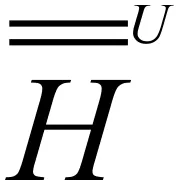
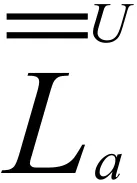
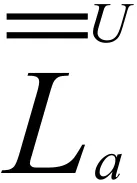
文中不加说明的U均指幂等元半格。
2 强U--富足半群上的同余及性质

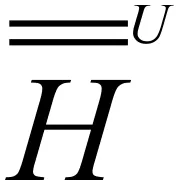

(2)(ab)*=(a*b)*,特别地,b=u∈U,(au)*=a*u;
(3)(ab)+=(ab+)+,特别地,a=u∈U,(ub)+=ub+。




(3)同(2)的证明。
引理2.2 若S为强U-右-富足半群,则

={(a,b)∈S×S|∀u∈U,(ua)*=(ub)*}





根据对偶性得
引理2.3 若S为强U-左-富足半群,则
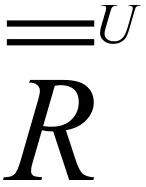
={(a,b)∈S×S|∀u∈U,(au)+=(bu)+}
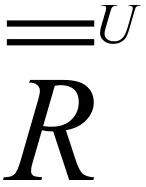
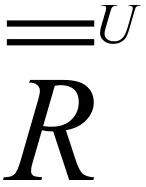
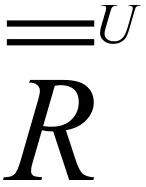
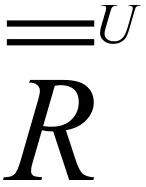
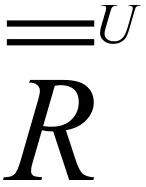
由引理2.2和2.3得:
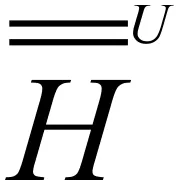

={(a,b)∈S×S|∀u∈U,(ua)*=(ub)*,(au)+=(bu)+}
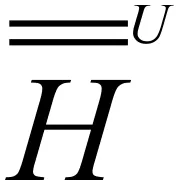
记
其中
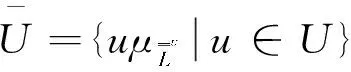




再证γ是同态映射。对∀u,v∈U,有

则得γ是同态映射。
综上知γ是同构映射。

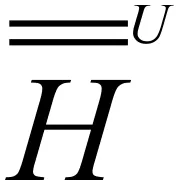
以下结论是本节的主要结果:
引理2.8 若S为强U-右-富足半群,则下列条件等价






对偶地有:
引理2.9 若S为强U-左-富足半群,则下列条件等价

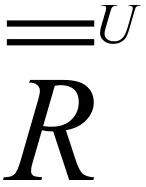
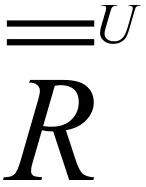
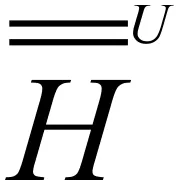
(1)对∀a∈S有a*=a+;

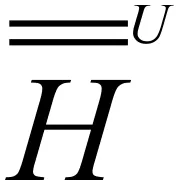
(4)U是S的中心。
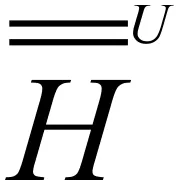
a+=(a*a)+=a*a+,
a*=(aa+)*=a*a+,
从而有a*=a+。


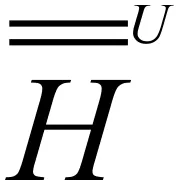
au=(au)*(au)=a*uau=ua*au=uau,
ua=(ua)*(ua)=ua*ua=ua*au=uau,
从而得au=ua,故U是S的中心。


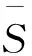




根据对偶性有: