基于修正傅立叶级数展开的非稳态振动信号分析

张武林，高文涛

(中国飞行试验研究院 飞机所，陕西 西安 710089)

0 引 言

直升机在执行机动飞行动作时，会受到突变力和力矩以及非对称气流的影响，进而引起直升机上某些部位的振动突变，突变后的振动量值有可能超出振动限值，进而对试飞安全构成威胁，所以准确获取非稳态信号的振动量值至关重要. 采用传统的FFT是以信号稳态为前提的，在对数据进行分析时，无法给出信号中所包含的非平稳信息.

20世纪80年代出现的小波变换是采用可以平移和伸缩的小波对信号进行处理，可以实现对信号局部时频分析的目的[1-4]，但在进行时频时未能给出信号真实量值. 陈钊和赵明等采用等角度重采样方法对动部件在转速发生变化时的振动进行分析，准确获取了过渡状态下的振动情况[5,6]； 吴吉利等提出了一种转子启停车过程中的基频振动分量提取方法，并成功应用于启停车过程中非稳态振动分析[7]； 赵慧敏和康海英等将经验模态分解应用于非稳态振动信号分析，并在此基础上实现了振动故障的智能诊断[8-10]； 汪伟分析了时域采样和角域采样的关系，并采用阶次跟踪方法对非稳态振动信号进行了分析[11].

本文采用修正后的傅立叶级数展开方法对直升机振动信号进行数据分析，提高了振动数据的分析速度，并能够准确地获取突变信号中的振动变化. 另外，此方法可以用于振动实时监控方案设计，以在试飞过程中对试飞员进行提醒，降低试飞风险.

1 直升机振动特性

相对于固定翼飞机，直升机除了可以执行滑跑起飞、爬升、平飞、盘旋、下滑等常规动作外，还可以执行垂直起降、悬停、侧飞、后飞等特种飞行动作，在执行任务过程中，直升机所承受的载荷类型更为复杂.

直升机振动信号由振动量值较大的离散成分与量值较小的宽频成分叠加形成，如图 1 所示，其中离散频率成分来源于各旋转部件的基频及其谐频，而宽频成分主要来源于气流作用于直升机引起的机体或部件振动. 由于直升机飞行速度较慢，由气流引起的直升机宽频振动在量值上明显小于离散频率的振动量值，在对直升机进行振动分析时，主要针对这些离散频点，确保振动量值在安全限值以下. 新研直升机或直升机动力系统都会针对这些离散频点对应的振动量值提出明确的限值要求，一旦超出限值要求，将会影响飞行安全. 为保证试飞安全，需对这些振动量值实时监控，以观察飞行过程中的振动变化情况.

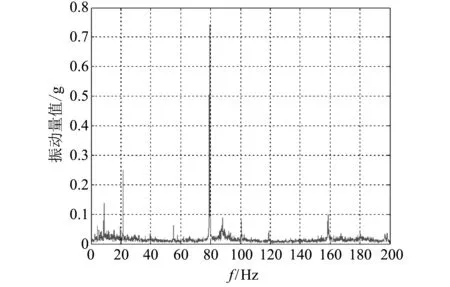
图 1 稳定平飞时尾减输出端振动响应Fig.1 Vibration response of the tail reducer when the helicopter is in stable horizontal flight

2 振动数据分析

2.1 基于修正傅立叶级数展开的分析方法

直升机振动分析主要针对离散频点，在数据分析时，可以根据每次分析频点的不同，采用傅立叶级数展开的方法，快速计算得到对应频点振动量值的变化趋势，傅立叶级数展开公式为

(1)

式中：N为单次展开计算时的数据长度；m为离散数据点的序号；n为分析频点对应的序号.

采用FFT或者傅立叶级数展开算法进行数据分析时，如果分析频率不能落在频谱某一频率点上，则计算结果误差较大. 为提高分析精度，需增加单次计算时的数据块长度，但增加数据块长度后，对于非稳态数据计算结果误差同样较大. 在某些飞行状态下，尤其是机动飞行时，直升机振动量值存在不稳定性甚至振动突变，针对这一情况，可以采用式(2)所示的修正后的傅里叶级数展开公式进行计算，以此来提高数据准确性.

(2)

式中：k为傅里叶级数展开公式中的修正系数.

采用修正前后的傅里叶级数展开算法计算得到的结果如图 2 所示，图 2 中数据所用仿真信号采用式(3) 生成.

图 2 傅里叶级数展开计算结果Fig.2 Calculation results based on Fourier series expansion

仿真计算时，数据长度N和采样率fs均取5 120，仿真信号包含21.3 Hz，80 Hz两个离散频率点，修正前80 Hz恰好落在频谱某个频率点上，其幅值为4 g； 但21.3 Hz未能落在频谱某个频点上，其幅值只有8.58 g，而实际幅值为10 g，误差达14.2%，并且分析频点距离频谱频点越远，误差越大； 修正后21.3 Hz也能落在频谱某个频点上，其幅值为10 g. 对比发现，不增加数据长度N，通过设置k可以大大提高计算精度. 但对傅里叶级数展开算法进行修正时，也存在两点不足：①k值越大，计算量越大； ② 修正后的傅里叶级数展开公式，可以准确获取关注频率处的结果，但其临近频率处的结果存在一定误差.

f(t)=10sin(2πf1t)+4cos(2πf2t),(3)

式中：f1=21.3 Hz；f2=80.0 Hz；t为仿真信号持续时间.

考虑到直升机振动分析时主要针对指定的离散频率，所以可以只针对相应频点进行展开计算，以减小计算量，节约计算用时. 另外，指定分析频率临近频点存在误差，但对指定频率的结果并无影响，所以修正后的傅里叶展开算法可以用于直升机非稳态振动分析.

2.2 修正傅立叶展开算法在非稳态数据分析中的应用

直升机旋转部件较多，这些动部件在机动飞行过程中会受到非对称载荷，进而引起振动突变，俯冲拉起过程中尾减输出端振动响应如图 3 所示，俯冲拉起过程对应的飞行参数如图 4 所示.

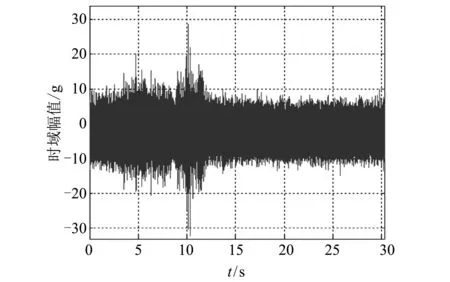
图 3 俯冲拉起过程中尾减输出端振动响应Fig.3 Vibration response of tail reducer in action of dive-hike

图 4 俯冲拉起过程中主要飞行参数Fig.4 Main flight parameters in action of dive-hike

由图 3 和图 4 可以看出在做俯冲拉起动作时，尾减输出端侧向振动响应变大，俯冲拉起动作结束后，振动响应恢复至正常值.

采用FFT对俯冲拉起段的振动数据进行计算,得到的频谱结果如图 5 所示. 采用FFT进行计算得到的是整个时间段内的均值，无法得到某一频率振动量值随时间变化的趋势，这是由于振动信号在进行傅里叶变换时舍弃了全部时域信息造成的. 另外对比图1还可以看出：除79.2 Hz处的频率峰值外，在79.2 Hz附近处的振动量值也明显增大，即79.2 Hz处的振动峰值已不再是离散单频峰值，而是窄带峰值，进一步说明在俯冲拉起过程中79.2 Hz 发生了频率偏移或者产生了新的振动峰值. 观察对应的飞行参数，在做拉起动作时，旋翼转速先增大后恢复，即在此过程中旋翼一阶频率先增大后恢复至正常值，由于频谱计算时采用的是FFT分析，每次计算的数据块长度为10 s，而旋翼转速变化过程只持续3 s，所以所得频谱结果并不能反应这一频率的真实量值，即FFT方法对于分析非稳态信号存在一定的局限性.

图 5 俯冲拉起时尾减输出端侧向振动频谱Fig.5 Vibration spectrum of tail reducer in action of dive-hike

为得到俯冲拉起过程中振动量值的详细变化情况，采用傅立叶级数展开的方法对上述信号进行分析，得到一阶频率和其对应振动量值的变化情况，如图 6 所示，一阶频率的变化情况如图 7 所示.

从图 6 可以看出：在俯冲过程中振动量值较大，在拉起后的稳定爬升段振动量值恢复正常，并且直接采用傅里叶级数展开算法计算得到的结果偏小，这主要是因为此时频率分辨率为1 Hz，导致频率上的振动能量分散到其他频率上造成的. 另外，在俯冲动作改出时一阶频率达到85 Hz，对应旋翼转速最大值达到106%，这一结果与图 4 相对应，并且采用修正傅里叶展开算法所得频率更为准确.

图 6 尾减振动量值曲线Fig.6 The first order frequency and the corresponding vibration value curve

图 7 一阶频率曲线Fig.7 First order frequency curve

在振动分析时，如果计算结果不准确，将无法对相应位置处的振动进行有效评价：计算结果偏小，认为距离限值较远，将会构成潜在的试飞风险； 结果偏大，认为余量不足，将会影响正常科目执行.

2.3 基于修正傅立叶级数展开算法的监控方案设计

综合上述分析可以看出，基于修正傅立叶级数展开的振动数据分析可以很好地给出离散频点的振动量值变化，由于可以只对离散频点进行展开计算，计算量较小，具有很好的实时性. 基于修正傅立叶级数展开算法的振动参数监控方案如图 8 所示，图 8 中只给出了单一参数监控时的相关信息，实际监控界面将根据需要监控的参数数目进行调整，对每个监控参数标示分析频率及实时振动量值，并绘制振动量值的历程曲线.

图 8 监控参数界面Fig.8 Monitoring parameter interface

基于傅立叶级数展开算法实时计算得到某一参数不同频点的振动量值，并进行曲线绘制，当振动量值接近或超过振动限值时，还可以由报警指示灯进行提示，以及时直观地对课题人员进行提醒，并与试飞员进行沟通，保证试飞安全.

除在俯冲拉起时旋翼转速会发生变化外，在自传下滑、地面开车不同状态之间切换时，旋翼转速也会发生变化，如果不能实时根据旋翼转速实时调整分析频率，将无法获取动部件旋转频率对应的振动量值. 针对这些特殊状态，可以在傅里叶展开计算时引入旋翼转速参数，对监控频点进行跟踪，获取对应频率的振动量值，此时式(2)中序号n采用式(4)确定.

n=round(n0R),(4)

式中：R为旋翼转速信号，且已以基础转速进行百分比换算；n0为基础转速时展开计算时某一离散频率对应序号；round为4舍5入取整函数.

3 结束语

基于修正傅立叶级数展开算法对振动信号进行分析：

1)可以在不增加数据长度的情况下，提高频率分辨率；

2)可以准确获得振动信号中包含的瞬态信息，为直升机的振动分析和评价提供了一种有效分析方法；

3)可以减小每次计算时的数据块长度，以实现对直升机关键频点进行实时监控，降低直升机的试飞风险.