基于矢量水听器的浅海背景噪声分析方法研究

刘 洋，李 然，杜敬林

(大连测控技术研究所，辽宁 大连 116013)

由于海洋环境的特殊性和复杂性，即使同一个海域，在不同的海况、季节、水文条件下，其海洋背景噪声场特性也存在巨大差异. 开展背景噪声噪声场矢量特征观测并基于测试数据进行统计分析是深入认识浅海环境特性的重要环节. 本文从浅海背景噪声理论出发，对背景噪声矢量特征进行理论建模，进一步结合试验观测数据进行了统计分析.

1 浅海背景噪声基础理论

按照发声机理可将海洋环境噪声分为4类：海洋动力噪声、海洋生物噪声、海洋中的人为噪声和海洋热噪声[1]. 引起海洋噪声的各种噪声源对海洋背景噪声的贡献差异主要体现在频率特性上，Wenz曲线将谱级曲线分为3段：海洋湍流、远处行船和风引起的海面扰动. 一般认为风生海洋环境噪声和行船噪声是海洋环境噪声的重要组成[2]，其能量分布在10 Hz～20 kHz频段. 远处航船噪声主要作用在10 Hz～1 kHz较低频段，而风生噪声则在数百赫兹～20 kHz频段，其中风关海面噪声起主要作用，其他噪声源如雨噪声的主要作用频段在几千赫兹至几十千赫兹. 可见行船噪声、风生噪声和降雨等间歇源对海洋背景噪声的贡献同时作用在几百赫兹～10 kHz的频段内，依具体海域噪声源强度分布以及声场传播的不同，它们在不同频率处于相互竞争的关系.

在一定的条件下，海洋背景噪声与海面风速具有高度相关的特点，Knudsen使用风生噪声模型对100 Hz以上海洋环境噪声作了分析，给出了以海况或风速作为参数的Knudson谱. 海洋背景噪声在数百赫兹到20 kHz的频段，谱曲线以约-17 dB/10倍频程的规律下降，并发现了在一定条件下不同频率处谱级和风速的对数都成线性关系，但线性程度有所差异. 可以认为风速和频率对噪声声压谱的影响是两种过程，海洋环境风生噪声声压谱P是风速υ和频率f的函数，大致上某一风速下风生海洋环境噪声谱级和风速的谱级-频率对数的关系以及某一频率下谱级-风速关系[3]，即P(υ,f)具有如下关系

P(υ,f)=υgfq.(1)

风生噪声谱级可表示为

SPL1(υ,f)=Glg(υ)+Qlg(f),(2)

式中：G=20lg(g),Q=20lg(q).

海洋背景噪声声压谱级SPL(f)则可以表示为

(3)

式中：SPL0为其它形式噪声源的贡献.

大量的实测海洋环境噪声谱级数据分析表明：对于某一海域某风速下频率为1 kHz以上的风关海洋环境噪声谱级-对数频率之间关系式，其谱级下降的斜率bf在风速变化时基本保持不变，即

(4)

著名的Knudsen 谱曲线和Wenz 谱曲线，以及国内实测结果均证实了这一点.

文献[4]给出了我国黄海、东海浅海域风关海洋环境噪声的谱级和海面风速的关系，如图 1 所示. 图 1 中每条曲线都是多次观测结果的平均值，其谱斜率约为-17 dB/10 oct或-6 dB/oct左右.

根据该关系，国内外学者提出了噪声谱级与风速对数的回归半经验公式，其合理性经过了许多实验的证明. 一般达到均衡海面状况和稳态过程中，线性回归是定量描述噪声特征的一种较好的方法. 但在实际海洋中引起海洋参数机理的多样性以及地域特殊性决定了特定频段海洋风生以及行船关系的复杂性. 首先，随着航运业和航船噪声的发展，人为海洋环境噪声源强度的统计平均值明显上升，不同频段以及不同强度风力和谱级的关系具有重要差异； 其次，影响深海环境噪声的因素相对浅海陆架简单，近岸的风场结构比开阔海域复杂； 再有，噪声场时变性会受噪声源时变空变性的影响，因此风生噪声并非在所有情况下占优势. 国内学者提出了考虑行船与V字形的风速模型[5]，将航船活动以及其受风速制约的作用同总噪声级联系了起来.

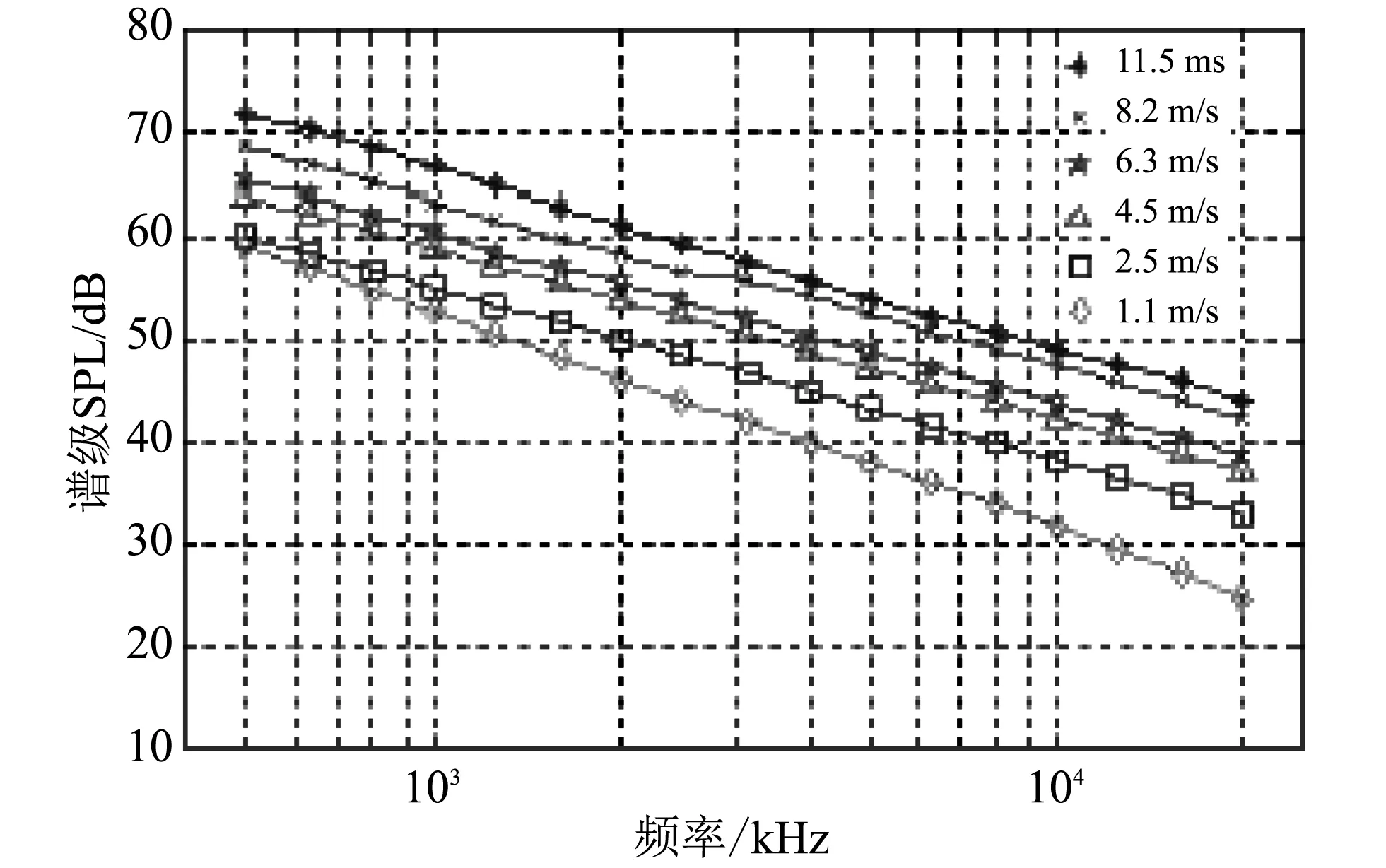
图 1 黄海浅海海域和东海某海域风关海洋环境噪声谱级Fig.1 The noise spectrum level of the ocean environment about wind in the Yellow Sea shallow sea and a sea area in the East China Sea

NL2=B(f)+20n(f)lgV,(6)

式中:NL1为航船噪声级；NL2为风生噪声级；Vk为转移风速；AfBf为常数；n为风生噪声回归系数；m为航船噪声回归系数.

2 基于矢量水听器的浅海背景噪声分析方法

针对浅海背景噪声观测、分析的需求[6，7]，设计了座底式矢量接收系统，分频段使用4分量低频和3分量高频矢量传感器获取20～10 000 Hz的海洋背景噪声数据. 其中4分量传感器Vz(t)方向朝向海底，3分量传感器Vz(t)方向朝向海底，其余方向由罗经及现场方位校准获得.

2.1 典型声压与振速频谱分析

使用功率谱估计的方法[8]给出各自传感器的声压及振速正交分量的自谱估计，得到海洋背景噪声声压谱级Sp2(f)和振速谱级SVx2(f),SVy2,SVz2(f)，以评价海洋背景噪声场在不同方位的强度以及声场的各向异性. 图 2 给出了典型的 20 Hz～10 kHz海洋环境噪声声压与振速1/3 Oct谱级，谱级量值以某一参考级给出.

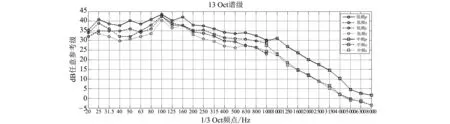
图 2 典型20 Hz～10 kHz海洋环境噪声声压与振速1/3 Oct谱级Fig.2 Typical 20 Hz～10 kHz ocean ambient noise pressure and vibration velocity 1/3Oct spectrum level

2.2 声压与振速比值谱分析

根据海面噪声模型可以推导出理论上声压和振速间的比值为

式中：n为待定系数，n通常取0.9～1.1，对应的声压与水平振速和垂直振速比值在对数运算后为5～6 dB和2～3 dB，而实际水体的值与噪声源的各向异性和具体的传播条件有关，需要试验测定.

就海洋噪声的来源考虑，风生噪声来自于波动表面，对于浅海有效作用的波动表面为5倍水深，因此风生噪声的主要来源方向应是垂直方向，当接收系统附近没有行船干扰时，Vz通道就体现了波动表面的真实信息，而远处行船噪声的方向多数来源于水平方向. 这样垂直方向声压、振速比值实际上体现了行船噪声与风生噪声之间的关系. 在行船噪声与风生噪声相竞争的频段内，很难从频率上区分风生噪声与行船噪声，这样，利用声压、振速垂直、水平各项异性的差异来区分风生噪声和行船噪声就显得较为有意义.

另一方面，经过同季节多组数据的对比，声压与水平振速的比值相对比较稳定，约为

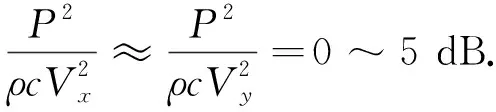
而声压与振速的垂直分量比值随季节变化相对剧烈，图 3 统计了典型的声压与振速垂直分量比值在不同季节、水文环境的结果.

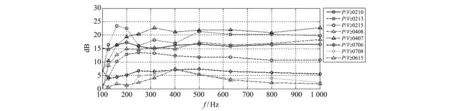
图 3 不同季节典型声压与振速垂直分量比值统计Fig.3 Typical ratio of sound pressure to vertical component of vibration velocity in different seasons

结果显示，声压与振速垂直分量的比值随频率变化的起伏在3～5 dB之内，相对较为稳定，但随季节起伏较大，不同季节从1～24 dB不等，也就是说声压谱级一定的情况下，振速的起伏与季节有很大关系，其最小值都出现在夏季禁渔期的6～7月份，值在1～7.5 dB之间，非禁渔期达到10～24 dB不等，而冬季行船较为稀少的2月也达到了10～15 dB.

根据良好水文浅海声传播计算结果，振速垂直分量Vz低于水平分量Vx和Vy约10 dB，这与冬季的测试结果相符. 夏季振速Vz有所提升，一方面行船的减少使得声压谱级下降，另一方面负梯度和负跃层水文环境下，下层的温度低于上层，使得声场垂直分量的比重增加，即负跃层和负梯度下声场垂直方向性极大值更多地偏向垂直方向.

3 浅海背景噪声与海洋环境参数的关系及统计模型

3.1 综合考虑行船风生噪声的海洋环境噪声统计模型

风生噪声是海洋背景噪声的重要来源，海洋环境噪声谱级与风速依赖关系的经典模型是Piggott提出的噪声谱级NL依赖于风速V对数的线性关系[9]，可以写成

NL=A(f)+20n(f)lgV,(10)

式中：A(f)为常数；n(f)为回归斜率.

该关系在许多深海地区得到了广泛的验证，一般说来影响深海环境噪声的因素相对于浅海大陆架来说相对简单，因此用高频段噪声谱和风速的依赖关系来观测和预报风速达到了相当高的水平. 然而在浅海区，风速并非在所有场合都是占绝对主导作用的因素，例如行船噪声会在特定频带和风生噪声形成竞争关系. 此外由于近岸的缘故，风场的结构情况较开阔海面复杂，加之噪声场的时变性(季节、周、日变化)会受到噪声源特性、空间分布以及水声信道特性的影响，必须综合考虑不同噪声源的时间、空间变化规律.

因此，综合考虑行船噪声NL1与风生噪声NL2的影响，建立模型

NL1=A(f)-20mlg(V),(11)

NL2=B(f)+20n(f)lg(V),(12)

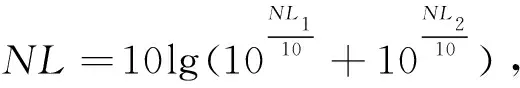
式中：A(f),B(f)为常数；n(f),m(f)为回归斜率；NL1是来自远处海面航船的贡献，与航道分布，在航船只数有关；A(f)代表了试验海区稳定的行船噪声级，而实际上航船噪声也受风速的制约，在观测中普遍发现风力增强到一定程度时出港的船只数会明显减少，因此会出现测量的噪声级反而比风力较低时更低的情形，在模型中用-20mlg(V)来描述. 因此，在特定的季节(航运、水文)条件下，风速达到一定的临界风速，NL1比NL2小时，风速将起到主导作用，临界风速和频率及不同季节的航运量有关. 对航运的调查需要耗费大量的资源，这里主要考察在临界风速以上海洋环境噪声随风速的变化情况.

3.2 环境噪声时变性与噪声成分分析

选择4月非禁渔期航运密度较大且风力变化较为丰富的时间，对海洋环境噪声及风速进行了连续观测，图 4 给出了座底式测量系统观测的日变化曲线. 观测数据从4月8日20：00到4月9日21:00，根据风力和行船规律将日变化分为两个阶段：

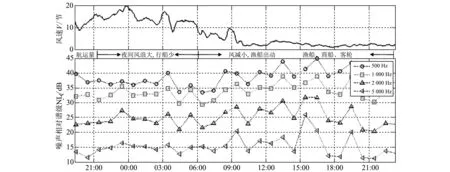
图 4 海洋环境噪声谱级与风速连续变化图Fig.4 Marine environmental noise spectrum level and continuous change of wind speed

第一阶段，4月7日20:00开始风力从10 kN开始增加，并在夜间00:00达到最大值20 kN，然后缓慢下降，到4月9日9:00下降到3 kN左右. 此阶段背景噪声谱级从500 Hz～5 kHz起伏较小(在5 dB以下)，并且日变化趋势与风速趋势相同. 在21:00～次日6:00风速较高时段海面风浪很大，小型渔船、商船很少出动，从水听器监听得到的结果显示，此时航运声音很小. 以上分析表明，这一阶段风生噪声起到了主要作用.

第二阶段，当4月9日7:00之后航运开始丰富，此时虽然风速较低，但噪声谱级持续增加，并且从500～5 000 Hz各频点的谱级均有较大的时变起伏，达到10～20 dB，不同频点谱级起伏的变化趋势和形状表现出很明显的周期相似特性，此周期性与风速监视无关，这是航船噪声具有的特点，监听及基于AIS的行船调查结果也表明航运量的增加. 以上分析表明，这段时期航船噪声是主要来源.

分析表明：500 Hz～5 kHz之间，在航运丰富的时段，风速在10 kN以下，谱级有较大的起伏，这时航运占主导因素； 当风速大于10 kN时，航运减小，谱级起伏减小，风生噪声是主导因素. 清晰地体现出风速变化条件下，风生噪声与航船噪声二者贡献间的竞争关系. 图 5 为当日矢量方向性的估计结果，方向性的监视表明：第一阶段趋于各向同性，第二阶段行船噪声的各向异性程度较强，主极大方向对应于航道位置.

图 5 1 kHz海洋环境噪声方向性时变图Fig.5 1 kHz marine environmental noise directional time-varying graph

3.3 噪声谱级与风速的依赖关系

图 6 给出了不同风速及航运密度下的海洋环境噪声频谱，可见在10 kN风速以上环境噪声与风速形成正相关规律，而风速在10 kN以下，海洋环境噪声与风速出现了相反的变化规律，8 kN风速时的行船噪声谱级在500 Hz～10 kHz范围内与20 kN的风生噪声相当，而3 kN风速时的行船噪声高于20 kN风速时的风生噪声.

图 6 不同风速及航运密度下的海洋环境噪声频谱Fig.6 Marine environmental noise spectrum under different wind speed and shipping density

对风速及噪声数据进行细致同步与平均处理[10]，图 7 给出了典型频点风速与噪声谱级的对应情况，选择风生噪声起主导作用的中等以上的风速，针对风生噪声回归模型为

NL2=B(f)+20n(f)lgV.(10)

使用最小二乘法对风生噪声进行拟合分析，推导出风生噪声的回归系数. 图 8 为典型频点风速的拟合回归结果.

分析结果表明，在10～20 kN风速条件下，1 kHz 以上风关噪声占主导，并且噪声谱级与风速的对数成正比，在当前的航运情况下，800 Hz 以下风关噪声起主导作用的临界风速高于10 kN. 表 1 给出了观测海区非禁渔期典型10～20 kN风速情况下1～10 kHz风关噪声回归分析结果.

图 7 谱级与风速的对应情况Fig.7 The correspondence between the spectral level and the wind speed

图 8 典型频点风速的拟合回归结果Fig.8 Typical frequency point and wind speed fitting regression results

f/ kHz11.251.622.53.15456.3810n0.50.70.91.01.11.11.00.80.50.50.4

4 结 论

本文依据浅海海洋背景噪声理论,利用基于矢量水听器的座底式海洋背景噪声观测系统获取了不同海况、季节、水文条件的背景噪声数据，并进行了数据结果分析：

1) 海洋背景噪声谱级随季节变化规律很大程度上取决于不同季节海洋环境声速分布以及风、行船、雨等噪声源的变化规律.

2) 通过声压与振速的比值谱可以体现出海洋环境声场的各向异性，海洋环境不同频率的各向异性差异明显.

建立了考虑行船风生噪声的海洋背景噪声统计模型，并推导出1～10 kHz风关噪声回归系数，为深入分析浅海环境特性提供技术支撑.