分析天平包装件随机振动仿真分析及优化设计

米男男， 李 光

(天津科技大学 包装与印刷工程学院，天津 300222)

近几年，电商发展迅速，许多商品都要经过装卸、储存、运输才能最终到达消费者手中。商品流通过程中受到的振动、冲击具有普遍性及严重性[1]。随着机械自动化的发展，冲击载荷引起的破损越来越少，冲击破坏准侧已经不能准确地描述包装损坏的机理，且导致过度包装的产生，并引起缓冲包装成本的增加[2]。包装件在流通过程中受到的激励大多是随机的，在引起精密电子设备失效的环境因素中，振动因素约占27%[3]。

随着计算机技术的发展，仿真技术也逐渐走向成熟，仿真技术的应用避免了试验量大、破坏性强、成本高等弊端。目前，对于振动特性的研究也逐步趋于通过仿真软件实现[4-7]，频域分析方法在平稳随机激励作用下的振动研究方面具有完善的理论依据及试验验证[8-11]，可以获得较为快捷且准确的结构响应[12-13]。李晓刚[14]通过Ansys Workbench对运输包装系统随机振动进行了频域分析，仿真结果全面反映了随机振动规律，为缓冲包装设计提供了理论依据。Aw等[15]利用ANSYS Workbench软件对电子设备防水罩进行仿真，并验证了试验的准确性。王志伟等[16]通有限元分析研究了包装件的随机振动特性，并通过试验验证了仿真分析的准确性。本文以分析天平包装件为研究对象，旨在用ANSYS Workbench对该精密电子仪器包装件进行动力学特性分析，模拟包装件整体振动过程，分析动态响应，找到运输过程中使分析天平破坏的因素，进行相应的优化设计。

1 有限元建模

1.1 包装件模型的建立

分析天平包装件主要包括分析天平、缓冲衬垫、外包装箱等三个部分，包装件尺寸为401×291.5×372 mm。由于分析天平三维实体模型比较复杂，在此采用Solidworks建立分析天平包装件3D模型，如图1所示。

简化模型有利于网格划分，节约时间，减少计算资源的消耗，提高计算精度。因此，应对模型进行合理简化，保留缓冲衬垫的结构状态，保留产品整体结构，在保证产品的结构刚度不发生明显变化的前提下，忽略小孔、倒角等无关紧要的细小特征[17]。通过Solidworks与ANSYS Workbench的直接接口将模型导入有限元软件中进行动力学特性分析。为保证后续计算正常进行，必须在Solidworks中对模型进行干涉检查；模型导入Workbench后，在DM模块对模型进行检查[18]。

图1 分析天平运输包装件模型Fig.1 Analysis of the balance transport package model

1.2 接触、材料属性设置

有限元分析中，装配模型中各个部件之间的联接关系将直接影响到有限元分析的结果。Workbench既可自动建立检测模型接触关系，也可根据实际情况，人为地定义接触的方式、算法和范围等内容。该软件中包括绑定、不分离、无摩擦、粗糙、摩擦等5种接触类型。本文分析天平各个零件、分析天平与缓冲衬垫、缓冲衬垫与角垫之间均定义为绑定(Bonded)，角垫与外包装箱定义为摩擦(Frictional)，摩擦因数为0.12。

分析天平包装件不同部分使用不同材料，每种材料有特定的参数设置。该包装件用到的材料有ABS树脂、碳铝合金、无铅化玻璃、EPS和瓦楞纸板，模型各部分材料具体参数的设置，如表1所示。

表1 材料参数Tab.1 Material parameters

1.3 网格划分

网格划分的形式和质量直接影响仿真结果的计算精度和计算规模[19]。在形式上，若结构简单，选择六面体单元；结构复杂则选择四面体单元。在质量上，一般网格划分越细，则计算精度越高，但网格划分过细则会影响计算速度，对计算机性能的要求也会越高，故在网格划分时应根据实际情况合理选择。分析天平模型比较复杂，故有限元网格划分时选用四面体网格，如图2所示，共计128 303个节点，69 598个单元。

2 随机振动分析

2.1 随机振动基本原理

随机振动分析(Random Vibration)也称功率谱密度分析，是一种基于概率统计学的谱分析技术。现实中很多情况下载荷都是不确定的，汽车、轮船、飞机等在运输过程中每次的振动载荷也不同。因此，由于时间历程的不确定性，从概率学角度出发，将时间历程的统计样本转变为功率谱密度函数(Power Spectral Density，PSD)。功率谱密度函数是随机变量自相关函数的频域描述，它是一条功率谱密度值-频率值的关系曲线，亦即载荷时间历程，能反应随机载荷的频率成分。随机振动分析是一种频域分析，需要首先进行模态分析，它可以是单点的或多点的，本文采用的是单点随机振动分析。

图2 网格划分Fig.2 Grid division

2.2 仿真结果分析

2.2.1 模态结果分析

模态分析采用Block Lanczo分块模态提取法，步长为2.5 s，固定约束加在缓冲包装底部。由于随机振动提供的路谱频率范围为0～230 Hz，这里要求解出包括230 Hz在内的所有的模态频率与振型，并进行模态拓展，分析结果见表2，振型图见图3。

表2 分析天平前七阶频率及振型Tab.2 Analysis of the balance before the seventh order frequency and mode shapes

图3 模态分析振型图Fig.3 Modal analysis of vibration modes

由图3可以看出，包装件发生较大变形主要在上层角垫和前方纸箱隔板的部分，最大变形分别为44.588 mm和572.48 mm。前者主要因为在实际运输过程中包装件的堆码造成；后者则是因为运输过程中长时间高频率的碰撞和挤压造成。这与实际情况相符合，同时说明有限元模型是合理的。

2.2.2 随机振动结果分析

在模态环境中进行随机振动分析，输入PSD G Acceleration激励，采用天津市普通公路路谱，如图4所示。加载在模态分析中约束的位置，方向选择垂直于包装件的方向(Y)，系统的阻尼比设置为经验值0.02，完成设置后进行求解即可。(汽车运输机振动加速度功率谱密度以垂直上、下方向为最大，代表特殊的运输环境)。

图4 功率密度谱Fig.4 Power density spectrum

图5(a)和图5(b)分别是模态分析和随机振动分析的等效应力云图，应力主要分布在分析天平底部，这些地方恰好是分析天平有缺口、孔洞、沟槽的地方，在有载荷的情况下必然会出现应力集中的现象。图5(a)和图5(b)所示应力云图是符合实际情况的，能正确反映随机载荷下的应力分布，这也进一步证明了有限元模型的合理性。

图5 等效应力云图Fig.5 Equivalent stress nephogram

仿真求解后提取出包装件加速度响应结果，如表3所示。根据表3中的数据可以看出，分析天平包装件在X，Y方向的加速度响应有效值比Z轴大得多。

表3 各方向加速度响应RMS值Tab.3 Directional acceleration response RMS value G

由于包装结构的特殊性，故只针对Y方向进行分析研究。提取出包装件在Y方向上的加速度响应分布云图和位移响应分布云图，如图6(a)和图6(b)所示，从图中可以看出，Y方向的最大加速度响应值位于角衬垫上。这说明在振动环境下，这些位置产生的振动能量最大，是最容易被破坏的位置，同时也是有待优化的地方。

图6 Y轴响应云图Fig.6 Y-axis response picture

3 优化设计

3.1 分析设置

采用Ansys Workbench的响应曲面(Response Surface)法进行优化，在50个设计点中挑出3个最优点进行分析讨论。

3.1.1 目标函数

优化设计的最终目的是在满足结构优良特性的前提下降低包装件的随机振动响应，延长疲劳寿命，减轻包装质量。即通过调整衬垫的厚度，减小振动时的振幅，增加模型的固有频率，由此来降低加速度响应值，提高产品的振动特性，并实现包装轻量化。把随机振动加速度响应值、方向性变形值和包装件质量作为目标函数，即min(P6，P7，P8)。

3.1.2 设计变量

通过调整支撑部件的厚度实现结构优化，这里只考虑角衬垫的厚度的影响(即只考虑Y方向响应值变化)，以缓冲衬垫角垫的各厚度尺寸参数为设计变量，即P1(优化中P1与该方向衬垫厚度呈负相关)、P2，P3，见图7。各设计变量的物理含义和初始值如表4所示。

图7 设计变量Fig.7 Design variables

表4 设计变量的物理意义和初始值Tab.4 The physical meaning and initial value of design variables

3.2 优化结果分析

3.2.1 灵敏度分析

灵敏度可以用来评定输入参数对输出变量的影响程度[20]。通过仿真分析得到的柱状图，如图8所示。从图8可以直观的看出，P1，P2，P3对Y方向的P6(响应加速度)和P7(最大变形量)影响比都较明显；而对于P8(质量)，P2对其影响比较明显，P1，P3则几乎没有影响。

图8 灵敏度分析Fig.8 Sensitivity analysis

3.2.2 响应曲面分析

图9是目标函数加速度响应值(P6)、最大变形量(P7)、质量(P8)和设计变量衬垫上侧厚度(P1)、衬垫下侧厚度(P3)的响应曲面分布图，因P3对P7，P8的影响很小，此处响应曲面图省略。由图9(a)可以看出，随着P3和P2的增加，P6是降低的；图9(b)中，P7与P1和P2都几乎呈负相关；图9(c)中，P8在一定范围内随着P2的增加急剧减小，而P1对P8几乎没有影响。因此，在一定程度上改变P1，P2，P3即增加衬垫的厚度，可以降低响应值。

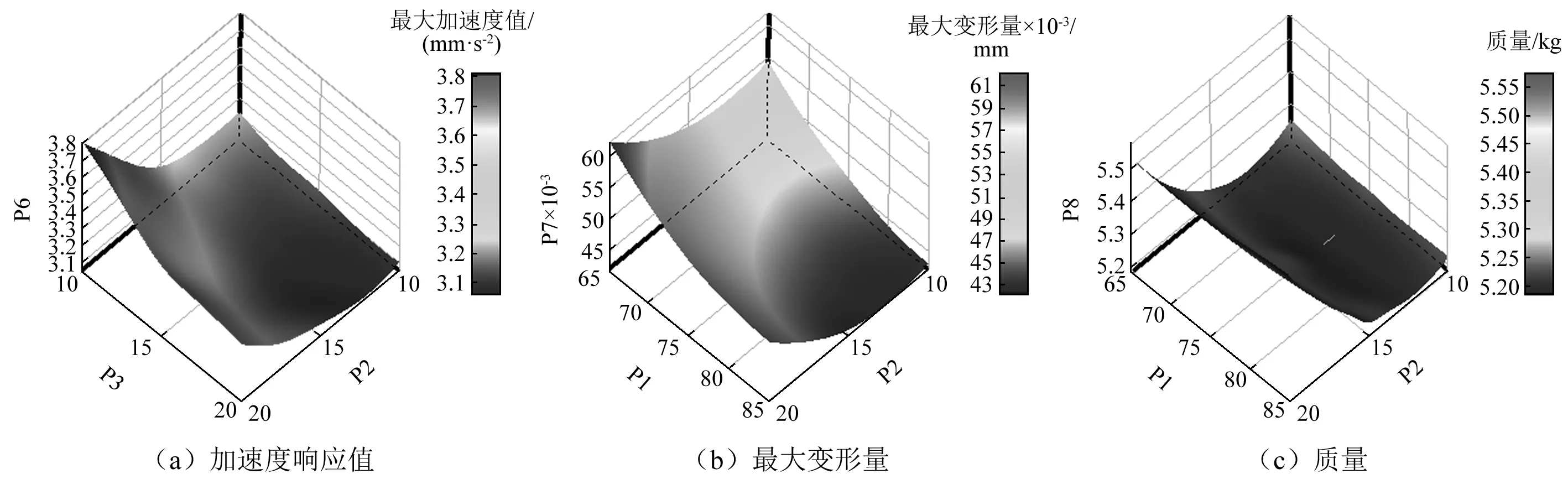
图9 响应曲面分布图Fig.9 Response surface distribution map

3.2.3 优化结果

灵敏度分析和相应曲面分析证实P1，P2，P3都将对目标函数产生较大影响，因此响应曲面优化时仍将P1，P2，P3作为设计变量。最终，系统从50组分析数据中给出三组最佳候选方案，如表5所示。可以看出，同等情况下候选点2质量最小，变形量也最小，加速度响应值也有所减小，比较符合优化目的，因此选择候选点2为优化设计点。

表5 最佳候选方案Tab.5 Best candidates

3.2.4 结果分析比较

根据表5中的目标函数取值范围和对优化结果的综合考虑，选取候选点2作为优化设计点。图10为优化前后包装件的固有频率，由图可以看出前六阶模态频率都有一定程度的增加，通过提高结构固有频率，避免结构在工作频带内发生共振，由此达到提高产品振动特性的目的。优化后的加速度响应云图及变形值如图11(a)、图11(b)所示。

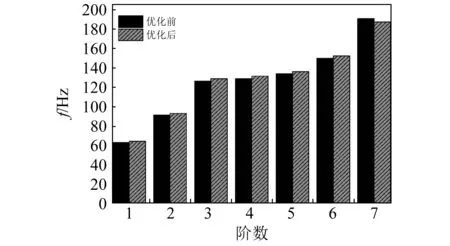
图10 优化前后固有频率对比Fig.10 Natural frequency comparison before and after optimization

图11 优化后Y轴响应云图Fig.11 Y-axis response after optimization

优化前后尺寸以及优化结果对比如表6所示。在振动条件下，包装件破损的本质是其在交变应力或应变的循环作用下形成振动疲劳[21]。优化后，包装件的整体应力的增加幅度为6.46%，整体应变的降低幅度为8.62%，最大变形值降低2.42%。应力增加说明材料吸收了更多的能量，那么内装物受到的能量会相应减少；而衬垫应变和变形量减小，相应的传递到内装物上的应变和变形量也会减小，这说明优化后的缓冲结构可以更好的保护内装物。

表6 优化前后参数对比Tab.6 Comparison of optimize parameters before and after

与设计候选点中预测的结果截然不同，优化后加速度响应最大值增加了1.86%。分别调出缓冲衬垫和分析天平的加速度响应曲线，如图12(a)和图12(b)所示，可以看出优化后前者的加速度响应峰值消失了，后者也在一定程度上避开了加速度响应共振峰值区，这对运输过程中的产品保护是有利的。

优化后缓冲衬垫厚度和缓冲衬垫质量都是减小的，每年产品包装数量数以亿计，每个缓冲结构的质量减小0.67%(3.6 g)，一亿个包装将节省360 t缓冲材料。包装的轻量化的同时也优化了包装件的动力学响应特性，可以降低运输途中包装的破损率，更好的保护内装物，同时，优化后的参数可以为隔振包装的设计提供参考，以提高运输途中包装产品的安全系数。

图12 优化前后加速度响应曲线Fig.12 Acceleration response curve of optimization before and after

4 结 论

以分析天平包装件为研究对象，用ANSYS Workbench进行动力学仿真，找出运输过程中缓冲包装的薄弱点，通过灵敏度分析得出影响包装振动特性的关键参数。用响应曲面法进行优化，从50个设计点中找出最佳优化点，通过优化前后参数值对比，表明振动特性有一定程度的提升，说明了仿真结果的可行性。由于输入的路谱频率范围较小，本试验结果也有一定的局限性。