脉冲型地震作用下独塔自锚式悬索桥碰撞响应试验研究

郑勤飞， 闫维明， 罗振源， 许维炳

(北京工业大学 工程抗震与结构诊治北京市重点试验室，北京 100124)

近些年来的地震灾害调查研究表明，碰撞问题是导致许多桥梁发生重大破坏的一个重要原因。例如，1989年美国Loma Prieta地震，旧金山—奥克兰海湾大桥引桥因相邻桥跨相对位移过大而导致某跨落梁[1]；1999年中国台湾Chi-Chi地震[2]、2008年中国汶川地震[3]，均有桥梁因碰撞发生落梁破坏；2011年新西兰基督城地震中，多座桥梁也遭受了严重的碰撞破坏[4]。

针对地震作用下桥梁结构梁端碰撞效应对桥梁地震响应的影响，国内外已有很多学者开展了大量的研究。如，Zanardo等[5]为研究考虑碰撞效应时多跨简支梁桥的地震响应，建立三维有限元模型，并采用非线性时程分析研究了碰撞间隙及地震动空间效应对碰撞效应的影响；王军文等[6-7]针对某连续梁桥，建立了有限元模型，研究了纵向地震作用下连续梁桥相邻联的非同向振动和伸缩缝处的碰撞效应；Wieser等[8]研究了一致激励下，连续弯梁桥的碰撞响应及给出了防止梁端碰撞的几个减震措施；雷凡等[9-11]以某座大跨三塔悬索桥为背景，建立了考虑碰撞效应的有限元模型，采用时程法研究了碰撞刚度、碰撞初始间隙等因素对碰撞效应的影响；禚一等[12]将Kelvin-Voigt模型和库伦摩擦模型相结合，通过一个摩擦元件来模拟发生纵向碰撞后接触点间的横向和竖向的相对摩擦作用；黄泰烈等[13]利用Midas/civil软件，通过建立有限元模型，对简支梁、连续梁和连续刚构桥梁地震碰撞模拟分析，揭示了桥梁地震碰撞的机理以及简支梁、连续梁和连续刚构桥梁地震碰撞的特点；李青宁等[14]进行了4组简化碰撞结构试验，通过数值模拟对其结果进行数值验证，研究了桥梁结构碰撞参数敏感性。总结已有的研究成果发现，目前针对碰撞效应对桥梁结构地震响应影响的研究主要局限于普通远场地震作用于梁式桥梁时的情况进行，且大多基于简化的有限元数值模型，缺少必要的试验验证数值模型计算的准确性，对近断层脉冲型地震作用下半飘浮体系的自锚式悬索桥碰撞响应的研究也未见有相关成果。

本文以某座典型的独塔自锚式悬索桥为背景，设计制作缩尺比为1∶20的试验模型，并选取了三条具有不同脉冲周期的近断层脉冲型地震波，进行了一致激励及行波激励下的地震模拟振动台台阵试验，对比研究了近断层脉冲型地震作用下考虑及不考虑碰撞效应时独塔自锚式悬索桥的地震响应特性，为自锚式悬索桥的抗震及减震设计与研究提供必要的参考依据。

1 模型试验概况

1.1 试验模型设计

本试验模型桥是以某非对称独塔双索面自锚式悬索桥为原型，原桥全长为370 m，跨径组合为35 m+135 m+165 m+35 m，塔全高126.5 m。主梁与索塔中横梁连接处设置单向滑动盆式橡胶支座，边墩及辅助墩处则设置有球形纵向活动钢支座。

模型桥设计时，考虑原型桥尺寸、试验场地条件及试验设备性能，拟定缩尺模型桥的几何相似比为1∶20，依据相似理论[15]确定缩尺试验模型桥其他相似系数，见表1所示。缩尺试验模型桥截面设计时并没有严格按照截面形式一致进行相似设计，而是在确保不影响真实模拟原桥动力特性的前提下，结合原桥中桥塔、桥墩和主梁等构件的构造和受力特点，以刚度相等、截面构造形式相同及截面形心位置相似为等效原则，对桥塔和主梁的复杂部位或构件进行简化设计。试验模型桥安装调试后的整体情况，如图1所示。

表1 模型试验的相似比

图1 试验模型桥Fig.1 Layout of the model bridge

1.2 振动台及传感器布置

本试验所用的加载设备为北京工业大学自主研发的地震模拟九子台台阵系统。该设备由九个1 m×1 m的振动子台组成，可根据试验需要进行任意方式组合以用于多维多点地震模拟试验，其主要性能参数如表2所示，试验模型振动台布置如图2所示。

结合本试验模型的受力特点，考虑振动台模拟地震试验的研究内容及目的，在模型桥位移响应较大及潜在易损伤区域布置测点。试验模型桥主要布置了941B型加速度拾振器、991B型位移拾振器、拉线式位移计、应变片以及力传感器。其中，941B型加速度拾振器及991B型位移拾振器用于测量主梁与桥塔的加速度与位移响应；拉线式位移计用以测量支座的位移响应；应变片用以测量桥墩、主塔及主梁关键截面处的变形响应；力传感器布置于梁端伸缩缝处，用于测量伸缩缝处主梁与桥墩间的碰撞力，传感器具体布置如图3所示。

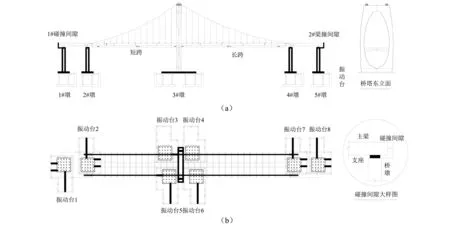
图2 试验缩尺模型及振动台布置Fig.2 Scale-reduced model and layout of shake tables

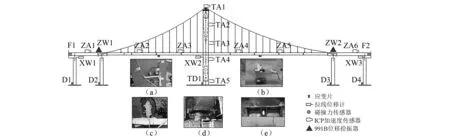
图3 传感器布置图Fig.3 Sensor layout

1.3 碰撞间隙设置

考虑到试验模型原桥在主梁两端(1#和5#桥墩墩顶处)均设置了宽度为300 mm的纵向伸缩缝，试验时将碰撞间隙设置于悬索桥主梁两端，并按表1相似关系计算，将初始碰撞间隙设置为15 mm，如图2及图4所示。为研究不同碰撞间隙下的碰撞效应，试验另外考虑了碰撞间隙为10 mm，20 mm两种情况，并分别进行试验。

图4 碰撞间隙Fig.4 Collision gap

1.4 地震波选取及试验工况设计

依据试验缩尺模型原桥所处场地的类别(II类)并根据《公路桥梁抗震设计细则》[16]选取三条具有不同脉冲周期的近断层脉冲型地震波，为更好对比不同地震作用下桥梁响应将三条地震波加速度峰值均调至0.7g(对应II类场地7度抗震设防烈度)，所选取的地震波信息，如表3所示。Cent波的加速度时程、速度时程及其傅里叶幅值谱，如图5所示。由速度时程图可知，脉冲型地震波具有显著的大速度脉冲，且由其傅里叶谱可知该地震波的卓越频率主要集中在低频段。试验时地震波以一致激励及不同视波速进行多点输入，分析脉冲型地震动作用下悬索桥的碰撞响应。考虑试验缩尺模型原桥所处场地的类别(Ⅱ类)并根据《公路桥梁抗震设计细则》中桥梁工程场地类别划分标准，所选地震波视波速分别取为V30=100 m/s，V30=200 m/s和V30=400 m/s。

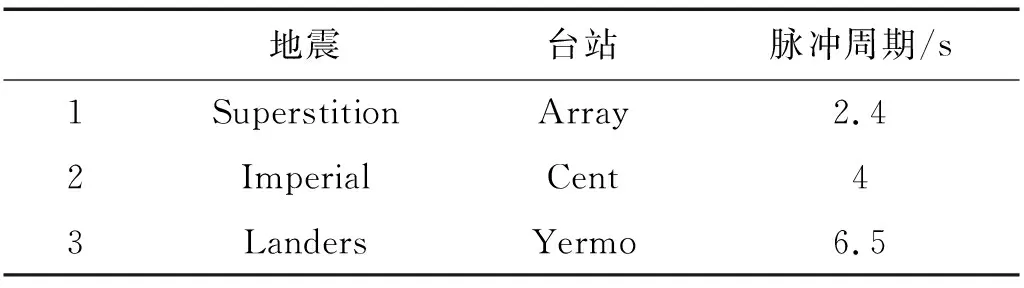
表3 试验地震波

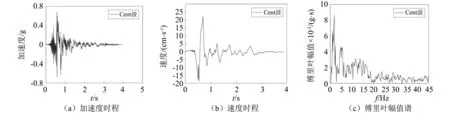
图5 Cent波的加速度时程、速度时程及其傅里叶幅值谱Fig.5 Acceleration time history, velocity time history and Fourier amplitude spectrum of Cent wave

2 试验结果分析

本文试验中采用FDD频域分解法识别了模型桥在纵向+横向白噪声激励下的模态信息，共识别出了前四阶振动模态信息，分别为主梁纵飘，频率为1.93 Hz；桥塔纵弯，频率为4.96 Hz；主梁对称横弯，频率为5.25 Hz；主梁反对称横弯，频率为5.78 Hz，且模型桥频率在试验前、试验中、试验后并未发生明显变化。模态识别结果如图6所示。

为判断振动台阵控制的准确程度，以Yermo波地震作用为例，给出了台面1和台面2的地震动的傅里叶谱，如图7所示。由图7可知，在0～25 Hz区间，实测不同台面地震动的频谱成分与输入的Yermo波略有差异，但由于模型桥主要阵型频率均远小于25 Hz，也即Yermo波卓越频带的绝大部分被振动台保留下来，因此不会影响本试验结果的准确性。

限于篇幅，本文仅通过1#和5#墩墩底应变、支座位移及主梁应变响应来说明试验悬索桥的碰撞响应特性。试验考察了不同碰撞间隙宽度、行波效应以及脉冲特性对独塔自锚式悬索桥碰撞响应的影响。为更好地衡量碰撞效应对悬索桥地震响应的影响程度，本文采用无量纲参数AF表示各工况下考虑碰撞时悬索桥各地震响应量的放大系数：AF=Rp/Rn，其中Rp为考虑碰撞时悬索桥各地震响应量峰值，Rn为未考虑碰撞时悬索桥各地震响应峰值。

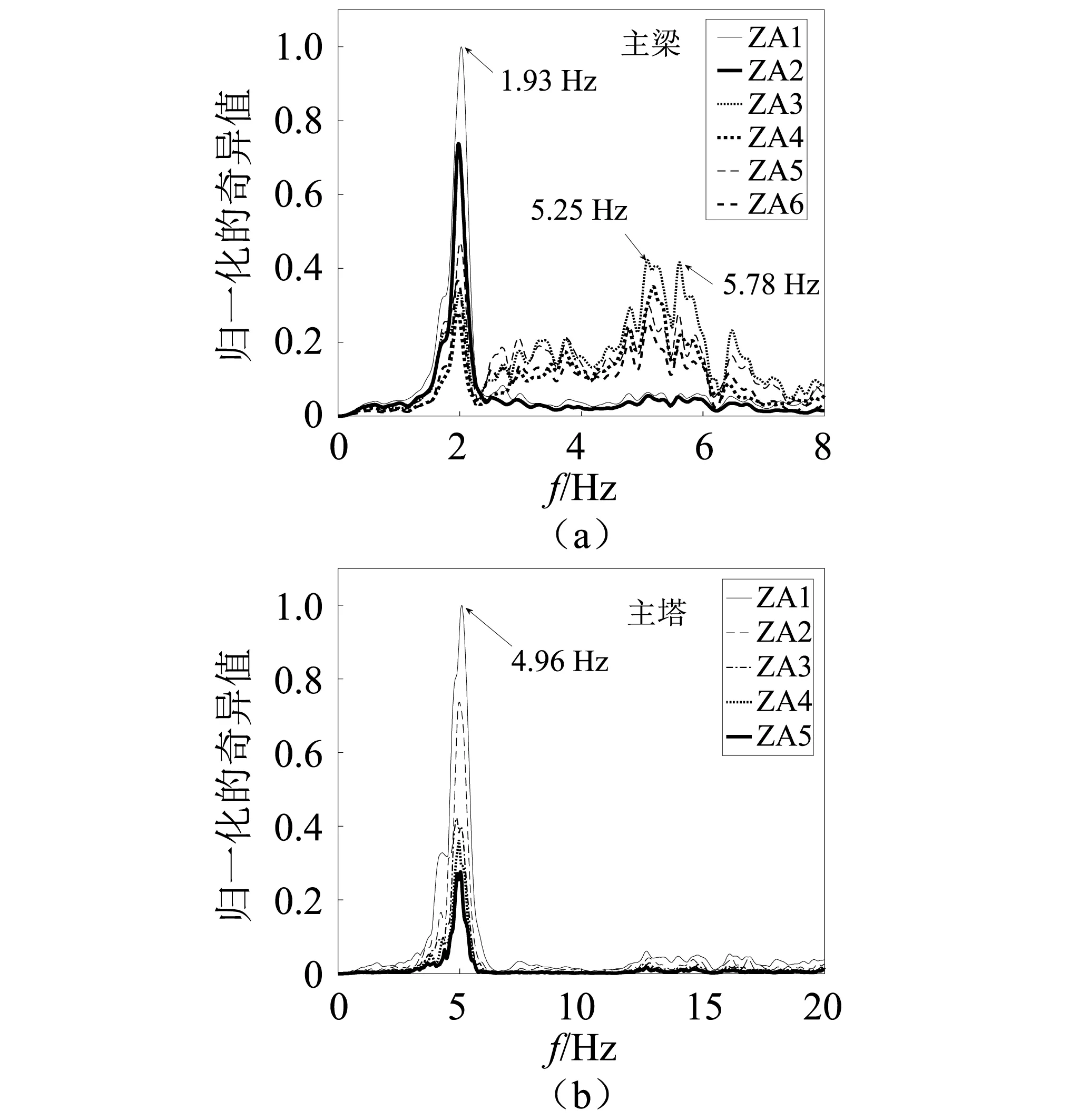
图6 模态识别结果图Fig.6 The results of modal identificati

2.1 不同间隙下碰撞响应分析

为了分析不同碰撞间隙宽度时悬索桥的碰撞响应，试验时分别考虑了碰撞间隙为10 mm，15 mm及20 mm三种情况。

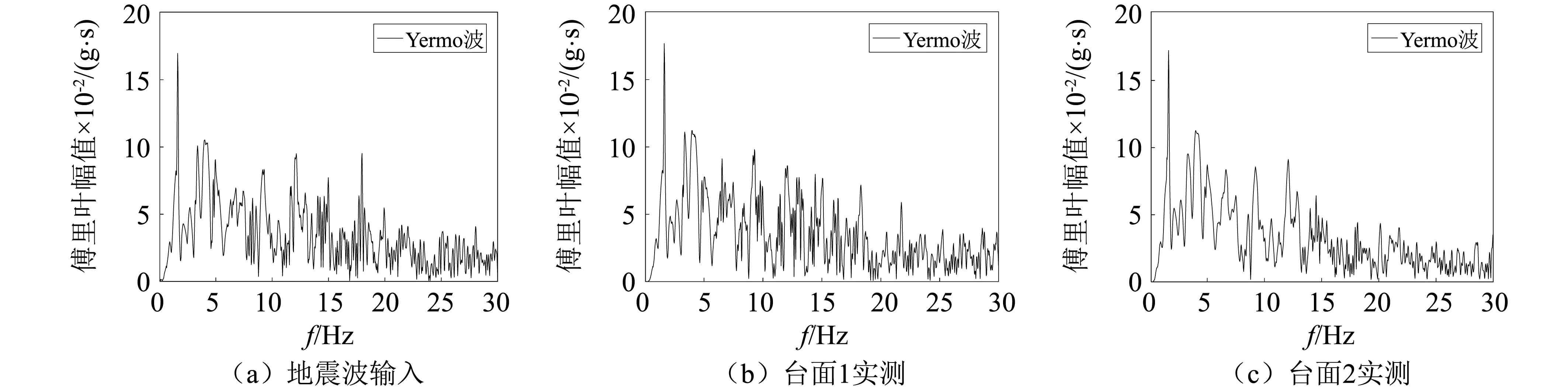
图7 台面地震动傅里叶谱Fig.7Fourier spectra of the seismic ground motions

三条地震波作用下不同碰撞间隙时1#间隙处的碰撞力峰值，如图8所示。图9给出了三条地震波作用下不同碰撞间隙时1#墩墩底应变响应峰值及未考虑碰撞时的墩底应变响应峰值，如图9所示。由图8可知，三条地震波作用下1#间隙碰撞力均随碰撞间隙的增大先增大后减小，且变化规律基本一致，碰撞间隙为15 mm时碰撞力最大，是碰撞间隙为10 mm和20 mm时碰撞力的1.23～1.31倍。王军文等对非规则桥梁在梁端伸缩缝处的碰撞进行参数研究时也指出：间隙比(间隙与最大支座位移比值)较大和较小时碰撞力较小，而间隙比在0.3～0.6时碰撞力较大，所得结论与本试验结果基本一致。由图9可知，试验所用任一地震波激励下考虑碰撞时1#墩墩底应变均明显增大，且此放大效应受碰撞间隙影响：碰撞间隙为10 mm时，1#墩墩底应变放大系数AF为1.71～1.88；碰撞间隙为15 mm时，1#墩墩底应变放大系数AF为2.07～2.19；碰撞间隙为20 mm时，1#墩墩底应变放大系数AF为1.47～1.65。在数据分析时发现：2#间隙处的碰撞力峰值与1#间隙处的碰撞力峰值表现出相同规律，2#，3#，4#，5#墩墩底应变响应与1#墩底应变响应具有相同规律，限于篇幅，本文就不在进行赘述。

考虑到实际桥梁结构中，梁端处伸缩缝即为地震作用时桥梁结构的碰撞间隙，因此，伸缩缝宽度值的确定除了满足必要的静力性能要求，也有必要考虑其对桥梁结构抗震性能的影响。

不同碰撞间隙时，1#，3#和5#支座的位移峰值及主梁位移峰值，并与未考虑碰撞时的情况进行对比，如表4所示。由表4可知，不同碰撞间隙时支座位移和主梁位移响应峰值均小于未考虑碰撞时响应峰值，其主要原因是当梁墩发生碰撞时，梁墩之间起到相互限位作用，从而使得支座及主梁位移碰撞响应较未考虑碰撞时有所减小。Kim等[17]在也分析研究中得到与本试验相似的结论：当主梁与桥墩碰撞发生时支座的相对位移会减小。

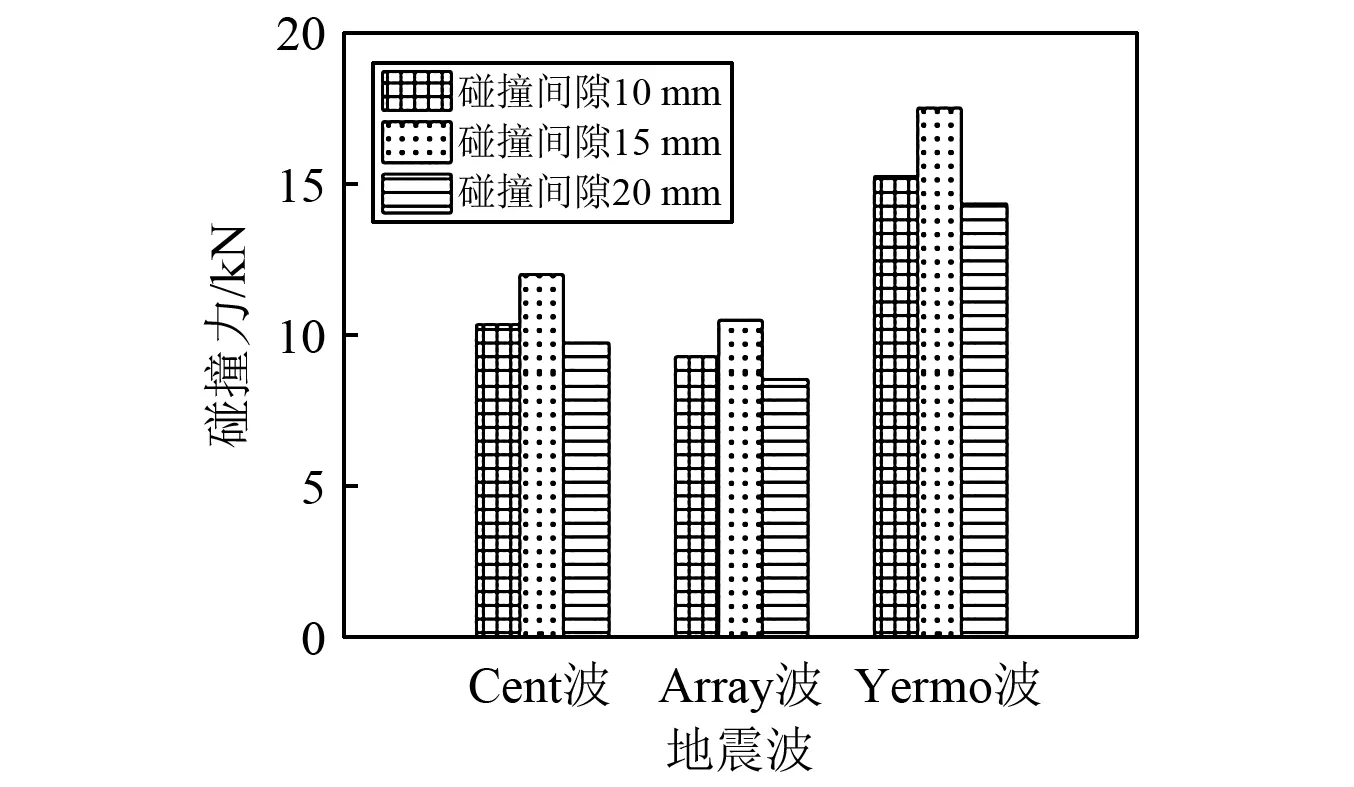
图8 三条地震波作用下1#间23隙碰撞力Fig.8 Collision force at 1# clearance under the action of three seismic waves

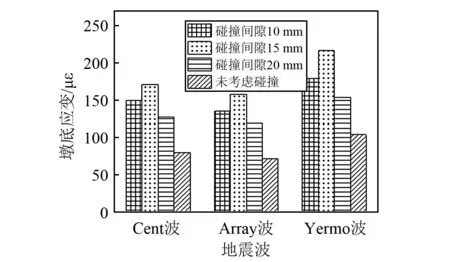
图9 三条地震波作用下1#墩墩底应变Fig.9 Strain force at 1# pier bottom under the action of three seismic waves

2.2 行波激励下碰撞响应分析

限于篇幅，仅对碰撞间隙为15 mm时模型桥在不同视波速下的碰撞响应进行分析。试验所用三条地震波分别以不同视波速输入下1#，2#，4#，5#墩墩底应变，如图10所示。由图10可知，墩底应变随视波速的增大先增加后减小，但不同视波速下的行波效应均较一致激励时放大了墩底应变响应，视波速V30=200 m/s时墩底应变响应放大效应最显著，其中1#墩墩底应变放大了1.34～1.38倍，2#墩墩底应变放大了1.43～1.50倍，4#墩墩底应变放大了1.40～1.55倍，5#墩墩底应变放大了1.36～1.44倍。三条地震波分别以不同视波速输入时主塔塔底应变，如图11所示。由图11可知，三条地震波以不同视波速激励时均放大了主塔塔底应变且主塔塔底应变响应放大效应随视波速的增大先增加后减小：视波速V30=200 m/s时主梁应变放大效应最显著，主塔塔底应变响应放大了1.32～1.39倍。行波激励时墩梁之间的运动产生相位差，使得墩梁间的碰撞效应更强烈，从而加大桥梁的碰撞响应，对此类桥梁进行抗震及减震设计时有必要考虑行波效应的带来的影响，以免低估了结构的地震响应。

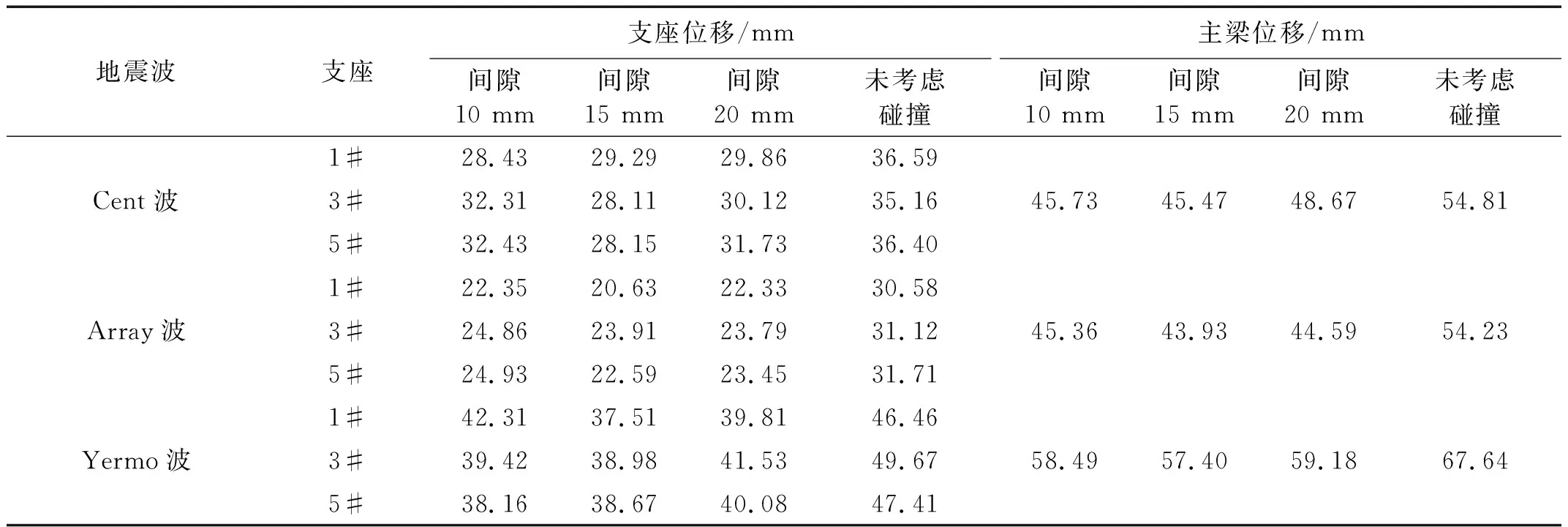
表4 三条地震波作用下支座位移及主梁位移响应峰值

图10 三条地震波不同视波速激励下墩底应变Fig.10 Pier bottom strain under excitation of three seismic waves with different apparent wave velocity

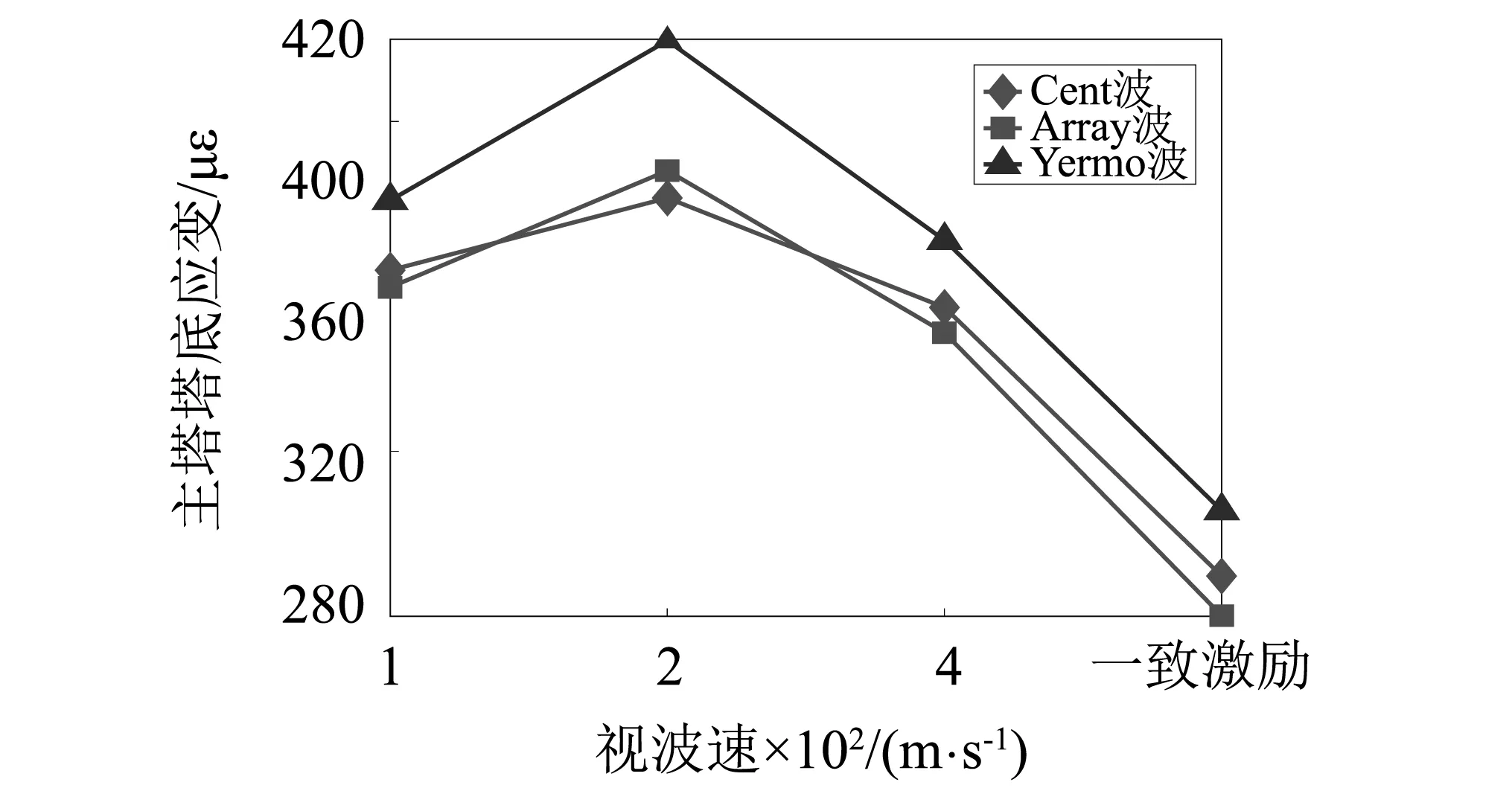
图11 三条地震波不同视波速激励下主塔塔底应变Fig.11 Main tower bottom strain under excitation of three seismic waves with different apparent wave velocity

此外，由图8～图11可知，Yermo波作用下模型桥各地震响应量均明显大于Cent波和Array波作用时模型桥的响应，这主要受地震波脉冲特性影响。由表1及表3可知，Array波、Cent波以及Yermo波压缩后的脉冲周期分别为0.204 s，0.34 s和0.553 s，而模型桥基本周期为0.518 s，可知，Yermo波的脉冲周期与悬索桥主梁基本周期最接近，在其激励下，模型桥产生共振响应，说明脉冲地震动的脉冲特性也是影响桥梁结构碰撞响应的重要影响因素。

3 结 论

本文对一座缩尺比例为1∶20独塔自锚式悬索桥缩尺试验模型进行了地震模拟振动台阵试验，试验选取了三条具有不同脉冲周期的近断层脉冲型实录地震波，并考虑碰撞间隙宽度、行波效应等因素对模型桥碰撞响应的影响，得到以下结论：

(1) 碰撞效应会显著增加模型桥边墩墩底变形，但会不同程度降低支座的位移响应。

(2) 模型桥梁端碰撞效应随碰撞间隙的增加先增强后减弱，此类桥梁伸缩缝宽度的设置有必要考虑对其抗震性能的影响。

(3) 行波激励会加剧梁端碰撞作用，使碰撞效应对边墩墩底变形和主塔塔底变形的放大作用更显著，对此类桥梁进行抗震及减震设计时应当考虑行波响应的影响。

(4) 脉冲型地震动的脉冲周期与模型桥主梁的纵向基频越接近，碰撞效应越强，对边墩墩底变形及主塔塔底变形的放大效应越显著，但对支座位移降低程度的影响不明显。