水泵水轮机飞逸工况下尾水管涡带演化研究

李琪飞， 赵超本， 龙世灿， 权 辉

( 1. 兰州理工大学 能源与动力工程学院, 兰州 730050；2. 甘肃省流体机械及系统重点实验室，兰州 730050)

应用于抽水蓄能电站的可逆式水泵水轮机在过渡过程中，有可能进入水泵制动、水轮机制动、飞逸和反水泵等工况[1]。其中，飞逸过渡过程属于大波动不稳定过程。处于飞逸的状态时，极有可能发生一系列由惯性附加动力引起的失稳现象。水泵水轮机尾水管的压力脉动是影响机组运行振动稳定性的主要原因之一。由于转轮出口涡流使得尾水管中心产生中心涡带，中心涡带附近压力脉动剧烈，从而会引起大幅度的振动和噪声。这些现象可能会对机组安全运行造成极的大威胁。

国内外的科研工作者利用各种试验方法和数值方法对水轮机尾水管内流动进行测试分析和模拟计算。1940年，莱因甘斯通过模拟试验，发现涡带最强烈时的压力脉动频率为转速的 1/3.6[2]。Favey等[3]进行了更为详细的试验着重研究了空化作用对压力脉动的影响。Jacob等[4]，将水轮机的运行工况分为典型的5个区域，总结运行工况与尾水管压力脉动的关系，其中部分负荷区的压力脉动幅值最大。Arpe等[5]通过混流式水轮机模型试验对尾水管内部流动进行了研究。吴钢等[6]研究了尾水管压力脉动与尾水管进口流场以及导叶开度的关系。他们在模型试验的基础上分析了水压力脉动测试、流场测试以及初生空化观测等实测结果，研究水轮机活动导叶开度的变化对尾水管水压力脉动的影响。

近年来随着计算机技术和CFD技术的发展，目前已经有很多通过数值模拟来对水轮机尾水管涡带压力脉动现象进行研究[7-10]。这类研究多是利用CFD流场分析软件对水泵水轮机正常工况进行模拟[11-14]，对于水泵水轮机飞逸过渡工况下尾水管内流动特性研究较少，为了深入了解尾水管涡带对尾水管振动噪声以及能量损失的影响。本文研究水泵水轮机飞逸工况下水泵水轮机尾水管内瞬态流场特性，着重分析了导叶开度对尾水管涡带形状演变、压力脉动以及能量损失的影响。

1 模型建立

1.1 物理模型

本文计算所用某抽水蓄能电站的水泵水轮机模型主要几何参数，如表1所示。

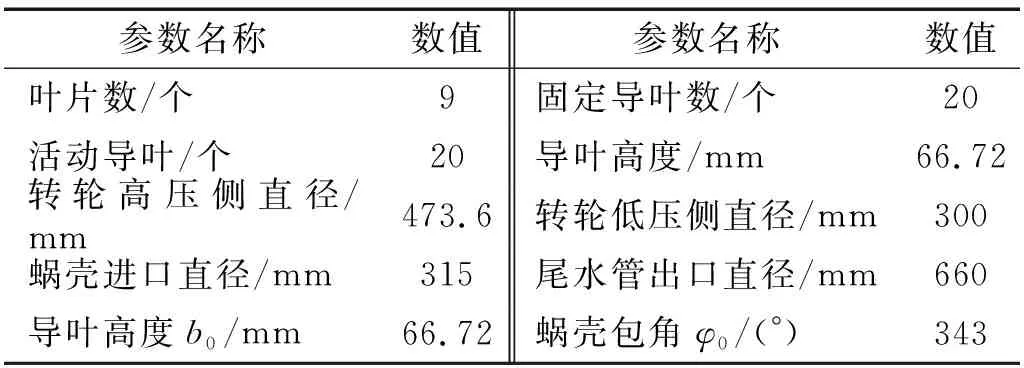
表1 模型水泵水轮机几何参数Tab.1 The geometry parameters of the pump-turbine

1.2监测点位置选择

监测点位置分别在蜗壳进口、转轮与活动导叶之间、转轮与尾水管交界面、尾水管锥段距活动导叶300 mm位置处、弯肘段管壁设置监测点，如图1所示。

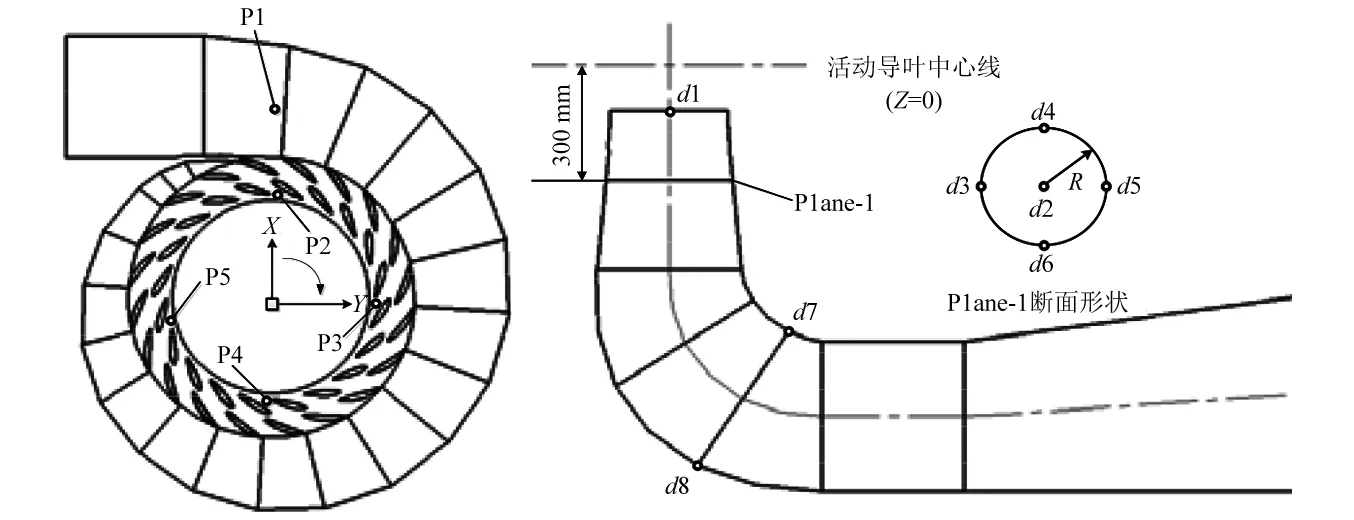
图1 压力监测和特征断面Plane-1位置Fig.1 Locations of pressure monitoring points pressure and the characteristic cross-section (Plane-1)

2 数值计算

2.1 网格划分

采用ANSYS-ICEM软件进行网格划分。由于偏离最优工况点，转轮进口的来流不是对称的，因此必须对全流道进行模拟[15]。由于蜗壳与固定导叶结构较为复杂，所以采用非结构化四面体网格以满足对复杂物理边界条件的适应要求，其他部件区域则采用六面体结构网格划分以保证较小的计算量和较高的精度。在转轮叶片、蜗壳导叶等壁面进行网格加密，网格尺度的选择保证满足湍流计算对壁面y+的要求。水泵水轮机各部分的网格划分及转轮叶片y+示意图，如图2所示。

图2 水泵水轮机的网格模型Fig.2 Mesh pattern of model pump-turbine

2.2 网格无关性验证

为了消除网格自身数量所产生的计算误差，需进行网格无关性验证。选择不同的网格尺度，生成7套不同的网格。取计算工况(a0=11 mm，Q11=0.115 0 m3/s，n11=57.51 r/min)，进行定常计算，通过对比效率特性，当网格数量达到550万个时，随网格数的增加，效率基本不发生变化，而且该工况下转轮叶片y+符合湍流模型要求。说明网格数的增加对数值计算结果影响较小，最终确定计算中采用的全流道总网格单元数为558万个，其中网格最小质量高于0.4，网格质量情况，如表2所示。

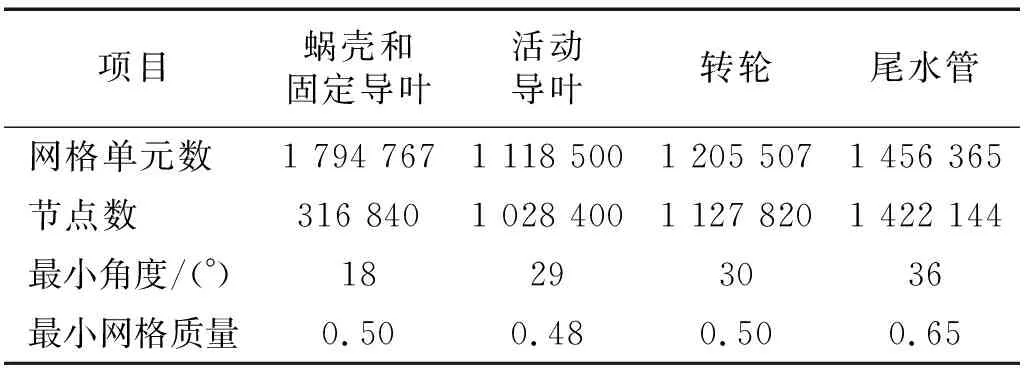
表2 各部件网格划分Tab.2 The grid division of each part

2.3 湍流模型与边界条件

由于偏工况尾水管内流动主要受漩涡结构控制，因此湍流模对尾水管流动的准确性有很大的影响[16]。Realizablek-ε模型在一定程度上考虑了流场各点的湍动能传递及流动的继承性，不仅能更好地模拟表面漩涡和附壁涡，而且在对压力脉动频率的预测结果中，Realizablek-ε方法与LES(Large-eddy Simulation)方法的结果基本一致。k-ω模型能准确预测分离特性，适合低雷诺数的近壁处理，但缺点是对入流条件很敏感[17]。SST(Shear Stress Transport)[18]模型在捕捉近壁面区以及远壁面区的流动特征，考虑了剪切应力的运输，不仅可以准确对来流进行预测，还可以精确的模拟分离现象，综合了k-ε模型非壁面区和k-ω模型的近壁面区计算有点。为了更加准确对飞逸工况尾水管涡带、压力脉动进行数值模拟，对Realizablek-ε，k-ω和SST进行模拟验证，验证结果如表3所示。由表可以可看出在飞逸小流量工况PO.1下k-ω模型水力性能较差，SST次之，Realizablek-ε误差最小。在正常流量PO.2下，SST水力性能最差，Realizablek-ε次之，k-ω误差最小。综合以上计算本文选择Realizablek-ε湍流模型ZGB空化模型进行数值模拟。根据工况所处的不同位置设置具体边界条件，如表4所示。

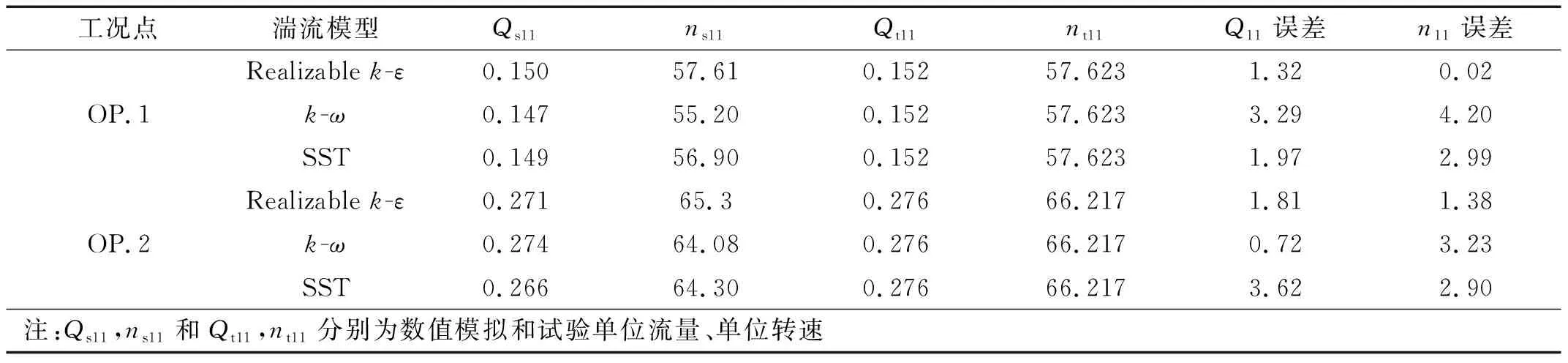
表3 计算结果与试验结果比较Tab.3 Comparison between simulation and test result

表4 边界条件Tab.4 Boundary conditions

2.4 步长设置

在非定常计算中，时间步长设置关系到计算精度和收敛速度。文中时间步长设置为旋转周期的1/120,每个工况均设置旋转10圈，取最后两圈结果进行分析。

3 模型验证

依据哈尔滨大电机研究所的试验数据，进行尾水管涡带演化的研究。此次试验水头Hm=30 m，该值是通过测量水泵水轮机进出口断面的压差所确定的[19]。以设计水头下模型水泵水轮机为研究对象，通过试验数据与模拟数据的对比来验证计算模型及计算方法的可靠性。本次选取了飞逸线上7个不同开度的工况点，如表5所示。通过已知数据算出其转速n以及进口质量流量qm，进行设置计算。

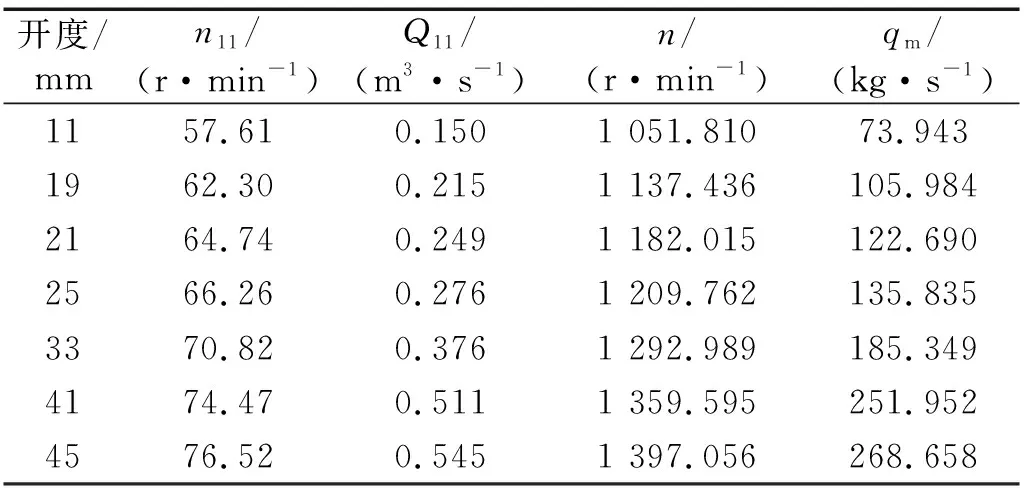
表5 定常数值计算结果Tab.5 Numerical simulation results of steady flow

计算出水头大小H(单位m)，通过式(1)和式(2) 换算出单位流量Q11和单位转速

(1)

(2)

式中：n为转速，r/min;D2为转轮名义直径，m；Q为计算流量，m3/s。n11与试验所得飞逸曲线进行对比结果如图3(a)所示。试验结果与数值模拟结果吻合良好，说明数值模拟方法和计算模型可靠。

由于本文研究尾水管涡带对压力脉动的影响为了确保数值计算准确可靠，在此基础上进行非定常模拟，监测尾水管上游压力，计算其相对振幅并与模型试验进行对比，如图3(b)所示。由图3(b)可知，试验和模拟曲线走势相同，但是存在一定差别，差别较大主要分布在较小流量区域，随着流量增大，模拟数据和试验数据趋于吻合。这是因为小流量工况下水泵水轮机内流动紊乱，随机出现的旋涡等偶然因素加剧了流动非定常性对模拟和试验结果的影响，使得试验结果和模拟结果差别较大。同时这也受监测位置选取误差以及工况之间的误差的影响，由此也说明数值模拟可以较好的反应真实流动规律。

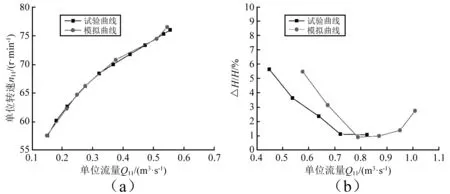
图3 试验模拟对比Fig.3 Comparison of calculated and experimental results

4 计算结果及分析

4.1 导叶开度对涡带形态及流场的影响

4.1.1不同导叶开度下尾水管内涡带形态变化

飞逸工况下，由于转速较大，发生一系列的由惯性附加动力引起的失稳现象，这些现象在尾水管涡带中表现较明显。不同开度下，一个涡带周期内，同一等压面涡态及该等压面速度的变化，如图4所示。由图4可知，随着开度增大，尾水管涡带形态分别经历紊乱柱状、锥状最后演变为螺旋状涡带。这是由于随着开度的增大，流量增加，涡带由紊乱变较稳定。但是随着流量的继续增加，由于转轮出口的环量增大，并且在转轮出口形成偏心矩，从而形成螺旋状涡带。

由非定常计算结果可以知尾水管涡带旋转周期大约为转轮周期的2倍(见图4)。当a0=11 mm时，涡带形态随着时间的变换较大，涡带形态由柱状逐渐下移变细，最后撕裂。这主要是由于小开度飞逸工况下，转速大、流量小使得涡带下移，当涡带下移发展到弯肘段时，由于速度方向发生骤变引起涡带分离；当a0=21mm时，涡带呈锥状，涡带形态随着时间基本不发生变化，锥状涡带很好的稳定于主轴方向没有偏移，这是由于随着开度的增加，流量增大转轮出口径向力对称分布；a0=41mm，涡带呈粗壮螺旋状，涡带主要集中于直锥段，形态随着时间有小幅度的变化。

4.1.2涡带压力等值面上速度分布

由图4等压面上的速度分布可得：在a0=11 mm时，从转轮出口、尾水管弯肘段到扩散段，速度先增大、后又减小，这由于流体进入弯肘段速度方向突然改变，涡带旋进方向改变而引起靠近弯肘段内侧速度增加。a0=21 mm时，等压面速度由尾水管直锥段上游到下游逐渐减小，涡带尾部溃灭于弯肘段高压区，这也表明涡带向下游旋进过程，受到弯肘段高压区的影响以及周围水流夹带卷吸的作用。a0=41 mm时，等压面上的速度由靠近尾水管壁面位置向涡带中心依次减小，这表明涡带发展到一定尺度会影响尾水管流体的流动特性，加聚近壁面涡带速度增大。

图4 飞逸工况下不同导叶开度下尾水管涡带形态Fig.4 The draft tube vortex form under the different runway status

4.1.3尾水管扩散段内回流

为了准确的研究小开度工况下尾水管内的流动特性，选取a0=11 mm，t5=T时刻做尾水管速度流线图，发现在距离轴线250～600 mm尾水管扩散端发现回流，并在其之间选取dt1～dt55个截面(距离轴线的距离b分别为250 mm,300 mm,500 mm,550 mm,600 mm)，并做速度矢量图观察其流动特性，如图5、图6所示。

由图6截面速度矢量图可得，5个截面速度矢量图均出现回流现象，说明在距离中轴线250～600 mm尾水管弯肘段下游存在局部回流，回流强度由两边向中间增大，这也说明回流是由涡旋引起。由截面速度矢量图方向演变以及整体流线图也可以看出局部回流是由涡带旋进尾水管弯肘段方向改变引起的漩涡回流。这也是造成弯肘段下游压力脉动，引起尾水管振动噪声的主要原因之一。

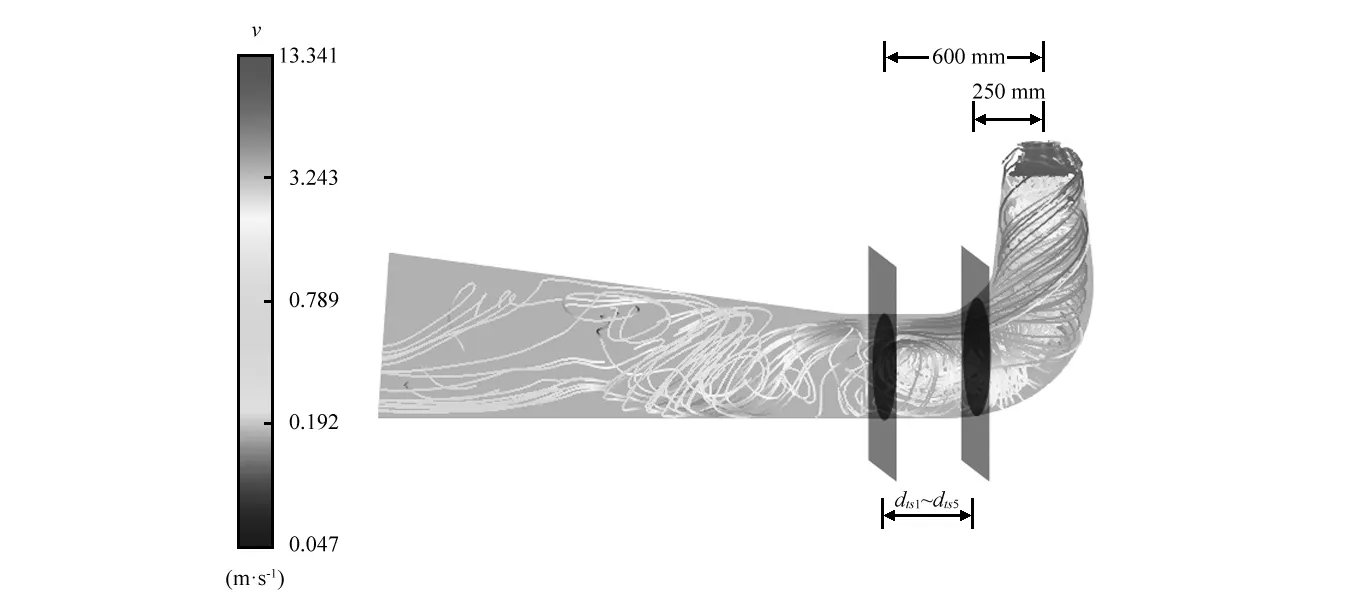
图5 尾水管整体速度流线以及截面分布图Fig.5 The distribution of the streamlines and cross-section of the draft tube

图6 特征断面速度矢量图Fig.6 Velocity vectors on the characteristic plane

4.1.4尾水管涡带对壁面湍动能的影响

为了进一步研究大开度条件下飞逸工况的粗壮螺旋涡带对尾水管直锥段的影响，特别是尾水管管壁区域湍动能，它可以反映尾水管管壁区域能量损失。所以选取a0=41 mm时，绘制t3=0.5T,t4=0.75T,t5=T时刻压力等值面速度云图，如图7所示。由图7可知，速度在螺旋涡带近壁面处较大，且集中分布在旋向面一侧。这主要是由于涡带随着转轮以一定的角速度旋转，与轴线距离越远其线速度越大。随着涡带发展，涡带与壁面之间的间隙变小会加剧速度的变大。同时随着尾水涡带的旋转，尾水管涡带不断撞击尾水管管壁(见图8)，引起尾水管管壁的转振动噪声以及尾水管区域水力损失。

为了研究涡带近壁面一侧高速流动对尾水管直锥段管壁的影响，通过距离尾水管进口面下游140 mm处的直锥段壁面周线上湍动能数据，并绘制其随x方向变化曲线(见图7)。对比等值面速度分布图和壁面周线x方向湍动能分布图，可得涡带转过1/2周期时，即涡带近壁面一侧靠近尾水管X=-0.2 m壁面时，壁面湍动能该处附近出现最大值；同时在t4=0.75T，t5=T时，涡带分别转过3/4个、一个周期，对应壁面周线湍动能最大值分别出现在X=0，X=0.2 m处，这说明尾水管涡带近壁面一侧处对应的其壁面周线上湍动能最大。这是因为尾水管涡带近壁面一侧速度较大，随着涡带的发展导致该位置壁面湍动能增大。湍动能主要来源于时均流，通过雷诺切应力做功给湍流提供能量[20],尾水管内壁附近和涡带中湍流从时均内吸收能量较多，即时均流在这两个区域能量损失较大，这种能量损失在涡带近壁面尤为突出，是尾水管内能量损失的主要组成部分。

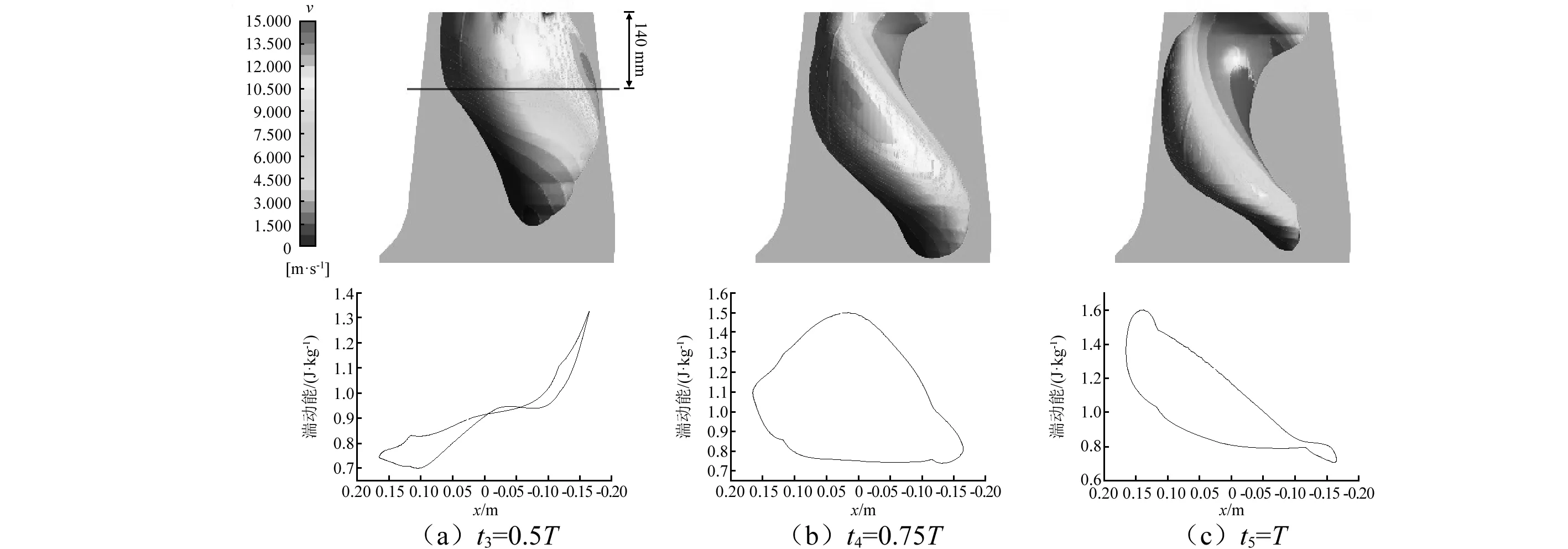
图7 压力等值面速度分布图、壁面圆周湍动能沿X方向分布图Fig.7 The velocity distribution on the pressure isosurface

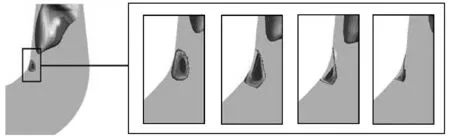
图8 涡带撞击尾水管管壁演化图Fig.8 Progress of the vortex hitting wall

4.2 尾水管压力脉动

尾水管中各监测点处的压力脉动时域图及频域图，如图9所示。以进口截面中心点d1为例进行分析，从时域图(见图9(a)～图9(d))可知，压力值明显随开度的增加而增大，这是由于在飞逸过程时，随着转速增加，尾水管内偏心螺旋涡的强度也增大[21]。频域图显示(见图9(e)～图9(h))，开度11 mm，41 mm时主频为8.77 Hz，幅值分别为835.09 Pa和3 515.74 Pa。开度21 mm时主频为4.38 Hz约为0.25倍的转频，与试验结果基本吻合，为其他两个工况的0.5倍，幅值小于其他两个工况，仅为393.63 Pa。a0=21 mm时尾水管压力脉动试验结果，如表6所示。

表6 尾水管压力脉动试验检测值(a0=21 mm)Tab.6 Experimental value of pressure pulsation of draft tube(a0=21 mm)

尾水管内其他各测点处压力脉动规律与其基本一致，只是在幅值大小上有所改变。对同一开度下不同监测点的对比发现压力大小随水流向下游流动的方向而增大。频率上在开度21 mm时尾水管中各测点压力脉动的主频均是4.38 Hz。但11 mm，41 mm时，监测点的位置不同其主频不同，监测点d1主频为8.77 Hz，这与涡带旋转周期相对应。监测点d3，d7，d8主频均为4.38 Hz。这是由于随着尾水管涡带向下游发展旋向速度降低以及其他扰动叠加的结果，同时结合“4.1”节尾水管扩散段内回流分析，说明飞逸点附近工况尾水管内部流动复杂，直锥段涡带螺旋旋转与扩散段回流相互作用，引发较大的压力脉动，最终使水泵水轮机运行不稳定。

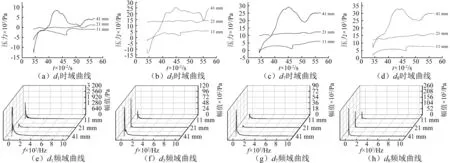
图9 尾水管中各处监测点的压力脉动Fig.9 The pressure fluctuations on each monitoring points in the draft tube

为了进一步分析飞逸工况涡带对压力脉动的影响，特选取最后两圈压力脉动频域图，如图10所示。这样选择可以过滤掉涡频等其他扰动的影响，从而更加突出尾水管涡带对压力脉动的影响。频域图显示，开度11 mm，21 mm，41 mm时主频为8.77 Hz，约为0.5倍转频，这与涡带旋转周期相对应。除主频外其他频率幅值均很小；这是因为选择两圈的时域过滤掉了频率较低涡频等杂频，涡带随着转轮的旋转成为了影响压力脉动的主要因素；当开度为41 mm时，同一个截面上中心点d2比壁面点d5幅值明显小，这是因为a0=41时，涡带形态呈粗壮螺旋态，涡带对尾水管直锥段压力脉动产生径向不对称影响所致；结合“4.1”节尾水管涡带演化，可知涡带演化的周期大约为2倍转轮旋转周期，这与其主频为0.5转频所对应，说明飞逸工况下尾水管压力脉动主要是由于涡带旋进所致。

图10 后两圈尾水管中各处监测点的压力脉动Fig.10 The pressure fluctuations on each monitoring points in the draft tube(the last two laps)

5 结 论

(1)由涡带压力等值面随着时间、开度的变化分析得出，飞逸工况开度a0=11 mm下涡带紊乱形状随时间变化较大；a0=21 mm时涡带呈锥状，时间对涡带形态影响较小；a0=41 mm时涡带呈粗壮螺旋态，形状随时间变化有小幅改变；流量是引起涡带形态变化的主要原因。

(2)飞逸工况下开度a0=41 mm时，随着涡带旋进，涡带近壁面旋向侧速度增大是导致直锥段壁面湍动能较大等能量损失的主要原因；a0=11 mm时，尾水管弯肘段下游流体发生回流主要是由涡带演化旋进尾水管弯肘段方向骤变引起的。

(3)通过尾水管内部流态与压力脉动分析：飞逸工况下开度越大尾水管压力脉动越强烈；尾水管直锥段主频与涡带旋转周期相对应，随着涡带向下游发展主频受涡频等杂频扰动的叠加作用；尾水管涡带旋转不断与尾水管壁发生碰撞，产生压力脉动，引起尾水管振动噪声，影响机组稳定运行。综上尾水管涡带是引起尾水管压力脉动的主要原因。