基于加权最小二乘法辨识的后缘襟翼智能旋翼振动载荷闭环控制仿真研究

周金龙， 董凌华， 杨卫东， 刘士明

(1.南京航空航天大学 航空宇航学院，南京 210016； 2. 南京模拟技术研究所，南京 210016)

直升机的振动水平普遍高于同时代的固定翼飞行器，过高的振动水平不仅会降低驾乘人员舒适性，还会对机载设备的寿命和可靠性带来不利影响。因此如何降低直升机的振动水平一直是直升机动力学研究的热点。

直升机的振动主要来源于旋翼、发动机、主减速器以及尾桨等旋转动部件，其中旋翼是最主要的振源。直升机桨叶为细长弹性梁结构，在直升机前飞时，由于旋翼前行侧和后行侧气流不对称，前行桨叶气流压缩、后行桨叶动态失速等会引起桨叶结构振动；此外旋翼桨涡干扰会在桨叶上产生冲击载荷，也会带来严重的振动和噪声问题。如果能从源头上抑制旋翼传递至直升机机体的通过频率振动载荷，减振效果将是非常显著的，并且可以降低机身振动抑制的实现难度。应用在旋翼上的振动控制技术可以分为被动控制和主动控制两大类。常见的被动控制如离心摆和双线摆等形式的动力吸振器，虽然结构简单，在设计频率减振效果明显且不需要外界能量输入，但是也存在减振频率单一、附加质量大的不足。

随着直升机技术的发展，对直升机振动水平限制的要求也越来越高，直升机振动主动控制技术越来越受到重视。根据技术实现途径的不同，应用于直升机旋翼系统的振动主动控制一般可分为控制自动倾斜器不动环的高阶谐波控制(Higher Harmonic Control, HHC)、主动控制拉杆(Active Pitch Link, APL)、主动控制后缘襟翼(Active Controlled Flap, ACF)和主动扭转旋翼(Active Twist Rotor, ATR)[1]，其中主动控制后缘襟翼式智能旋翼在当前技术条件下最具工程应用价值。

后缘襟翼式智能旋翼桨叶的后缘安装有可以主动偏转的后缘襟翼机构，通过后缘襟翼的偏转改变桨叶气动载荷分布，抵消部分交变气动载荷，影响桨叶的气弹耦合响应，从而达到控制旋翼振动载荷的目的[2]。后缘襟翼的控制规律，包括襟翼偏转的频率、幅值与相位，决定了智能旋翼的振动控制效果，因而如何寻找后缘襟翼的最优控制规律是后缘襟翼智能旋翼研究的核心关键技术之一。

高阶谐波控制算法(Higher Harmonic Control Algorithm)发展自控制自动倾斜器不动环的高阶谐波控制智能旋翼，其原理相对简单且控制效果明显，被广泛应用于各类智能旋翼振动控制和仿真研究中[3]。在智能旋翼振动控制仿真计算时，在不考虑测量误差等因素影响的情况下，可采用差分方式通过数值计算直接得到系统的传递矩阵T，而在真实的智能旋翼试验中，由于测量误差的存在，通常采用辨识的方法获得系统的传递矩阵T，Jacklin[4]对多种不同的辨识方法进行了比较分析，证明了辨识方法的有效性，但是在其研究中采用了简单的一元分段函数表示智能旋翼系统特性，与真实的智能旋翼系统差别较大，难以直接对后缘襟翼智能旋翼的振动控制效果进行分析。

为此，本文建立了带后缘襟翼的旋翼气弹耦合动力学模型用来计算后缘襟翼偏转对振动载荷的影响，并考虑到实际智能旋翼试验中测量误差的存在，采用经典的高阶谐波控制算法，结合加权最小二乘法辨识系统传递矩阵T，开展了单后缘襟翼智能旋翼振动闭环控制仿真研究，为后缘襟翼智能旋翼闭环控制的工程实现提供参考。

1 后缘襟翼智能旋翼气弹耦合模型

1.1 气弹耦合模型建立

为了计算后缘襟翼偏转对旋翼振动载荷的影响，需要建立带后缘襟翼的旋翼桨叶气弹耦合动力学模型。智能旋翼在运转过程中，各部件相互之间作用比较复杂，难以直接采用牛顿定律建立运动方程，通常采用Hamilton变分原理建立整个系统的动力学方程[5-6]

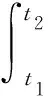
(1)

式中：δU为系统的虚位能；δT为系统的虚动能；δW为系统在运行过程中受到的外载荷虚功，由于后缘襟翼智能旋翼系统包括基体桨叶和后缘襟翼机构两部分，因此，虚位能、虚动能以及外载荷虚功可表示为基体桨叶和后缘襟翼机构两部分的叠加

(2)

(3)

(4)

对于带后缘襟翼桨叶，由于基体桨叶存在挥舞、摆振和变距运动，后缘襟翼还存在相对于基体桨叶的偏转运动，使得各个部件运动关系十分复杂，为了方便描述桨叶上质点的运动情况，建立了一系列坐标系用于描述桨叶上质点的运动，如图1～图3所示。

图1 桨叶变形前坐标系Fig.1 Undeformed blade coordinate system

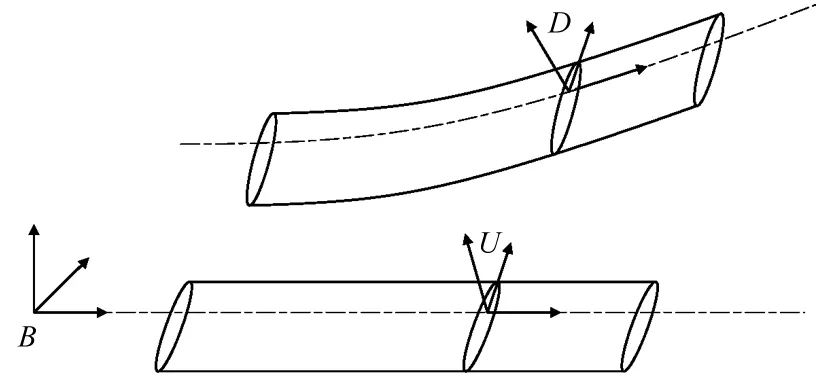
图2 桨叶弹性坐标系Fig.2 Elastic blade coordinate system

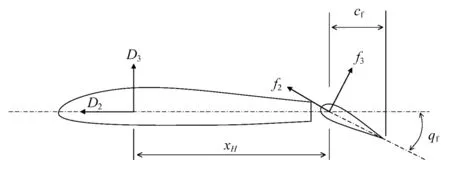
图3 后缘襟翼翼型坐标系Fig.3 Coordinate system of airfoil with ACF

图1～图3中:I为建立在桨毂旋转中心的惯性坐标系；H为建立在桨毂旋转中心的旋翼旋转坐标系；F为建立在挥舞铰处的桨叶刚体挥舞坐标系；L为建立在摆振铰处的桨叶刚体摆振坐标系；B为建立在变距铰处的桨叶变形前坐标系；U为建立在桨叶参考轴线x处的变形前的剖面坐标系；坐标原点位于桨叶参考轴线上；距坐标系B原点距离为x；D为坐标系U所在剖面变形后的剖面坐标系。

利用所建立的一系列坐标系，旋转桨叶某一剖面上点A相对于惯性坐标系原点的矢径表示为

(5)

(6)

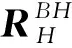
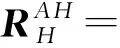
(7)

式中：xf，xc和xp分别为挥舞铰、摆振铰、变距铰相对于桨毂旋转坐标系、桨叶挥舞坐标系、桨叶摆振坐标系原点的偏置距离。在桨叶变形前坐标系B下，后缘襟翼剖面上一点A的矢径表示为

(8)

代入相应的坐标转换矩阵后，展开并整理得到

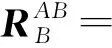
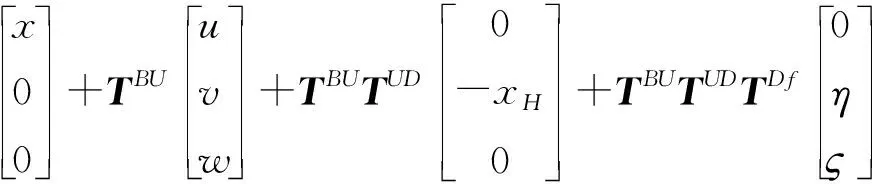
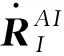
(10)

式中：虚动能δTf可表示为与广义自由度q对时间二次导数相关的线化质量矩阵M，以及非线性广义力FM的表达形式

(11)

同理对基体桨叶动能变分整理得到

(12)

基体桨叶的应变能来自于桨叶的弹性变形，其变分形式表示为

(13)

式中：ε为桨叶应变；σ为桨叶应力。相对于基体桨叶，后缘襟翼体积较小，而刚度较大，一般将其当做刚体处理，因此通常忽略后缘襟翼本身弹性变形应变能对系统运动的影响；在不考虑驱动机构特性的情况下，可忽略后缘襟翼约束刚度对系统应变能的影响

δUf=0

(14)

在桨叶工作过程中，受到的分布外载荷主要是气动载荷，气动载荷虚功表示为

(15)

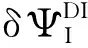
(16)

对于基体桨叶的常规翼型气动载荷计算采用查表法，根据翼型剖面的气流速度和迎角，查询标准的气动力系数表格，通过插值的方式获得对应速度和迎角下的气动力系数。而对于带后缘襟翼翼型的气动载荷计算，采用准定常Theodorsen带襟翼翼型气动模型[7-9]，升力系数、阻力系数和后缘襟翼铰链力矩系数分别为

(17)

(18)

(19)

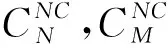
(20)

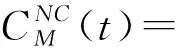
(21)

(22)

在得到了带后缘襟翼桨叶动能、应变能和外载荷做功的变分形式后，根据式(1)得到旋翼的气弹耦合动力学方程，利用形函数插值离散，组集旋翼气弹耦合有限元动力学分析模型，通过方程求解得到桨叶的气弹响应，进而通过力积分法计算桨叶结构振动载荷。

1.2 模型验证

由于缺乏完整的后缘襟翼智能旋翼试验数据，难以直接使用智能旋翼试验数据对本文模型进行检验，为了验证所建立的旋翼气弹耦合模型的计算精度，采用可获得公开数据的SA-349直升机飞行试验进行对比分析[10]，旋翼参数如表1所示，所对比的飞行状态如表2所示。

表1 旋翼参数Tab.1 Rotor parameters

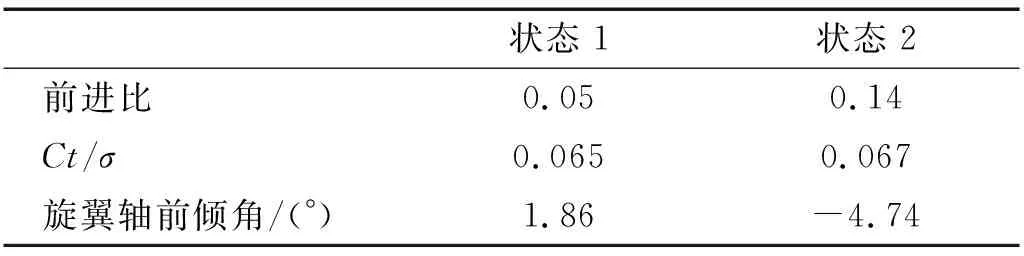
表2 飞行试验状态Tab.2 Flight test conditions

本文对不同飞行状态下桨叶剖面挥舞弯矩进行了计算，并与飞行实测数据进行对比如图4和图5所示。

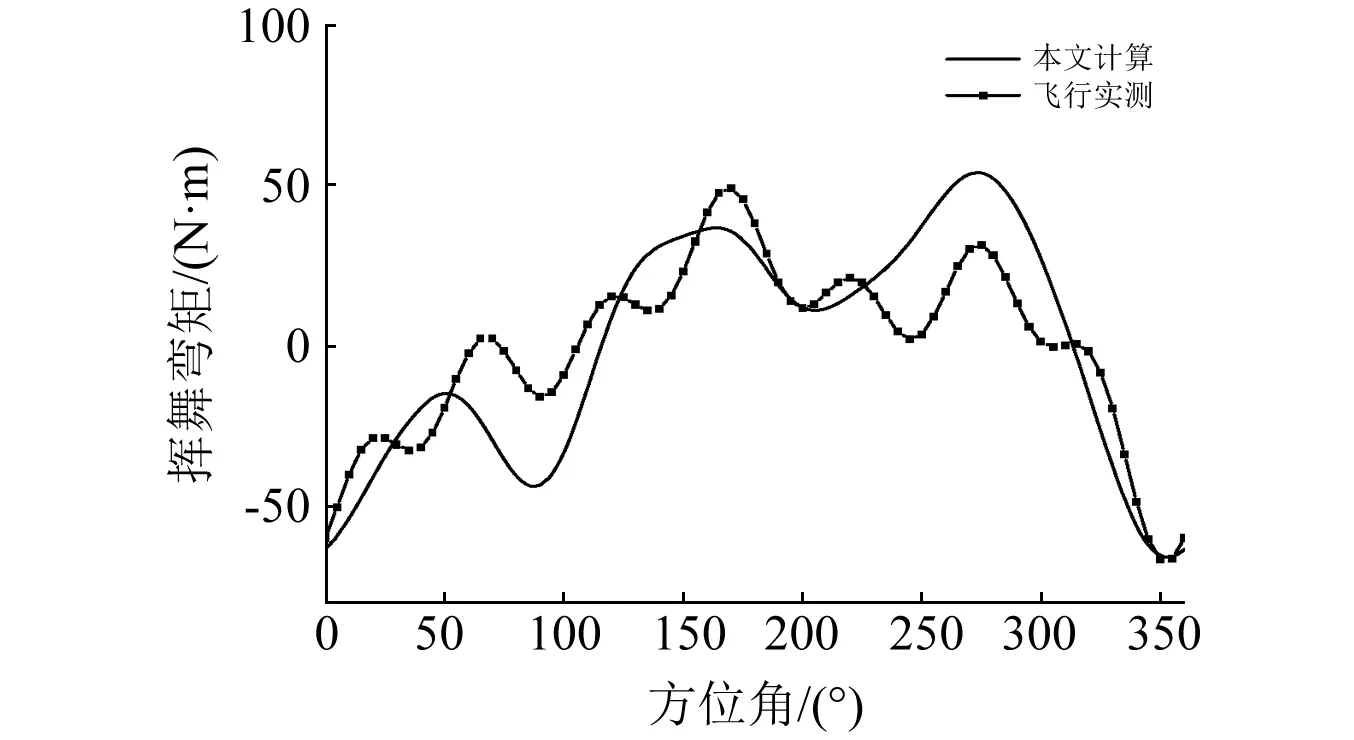
图4 挥舞弯矩(μ=0.05R,0.54R)Fig.4 Flap bending moment(μ=0.05R,0.54R)

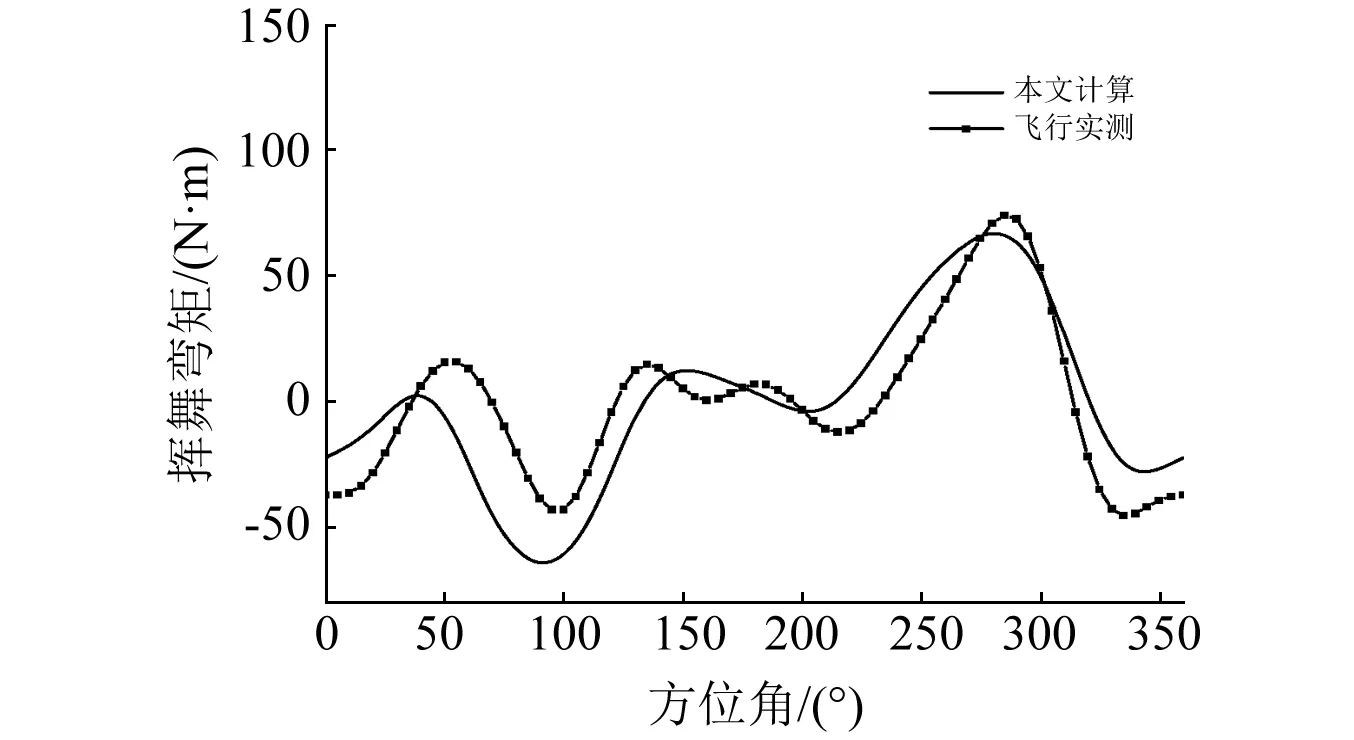
图5 挥舞弯矩(μ=0.14R,0.54R)Fig.5 Flap bending moment(μ=0.14R,0.54R)

通过与飞行实测数据的对比，可以看出本文建立的桨叶气弹耦合动力学模型能够精准地捕捉到桨叶载荷的变化，可以用于旋翼振动载荷仿真计算。

2 振动开环控制仿真研究

本文以SA-349直升机旋翼为基准，在其桨叶后缘布置单片后缘襟翼，组成带后缘襟翼智能旋翼模型，襟翼参数如表3所示。

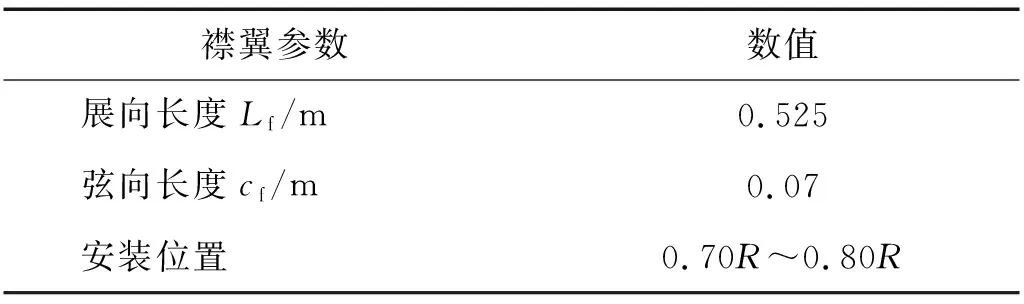
表3 后缘襟翼参数Tab.3 Parameters of ACF

根据旋翼桨毂载荷传递规律，桨叶作用到桨毂上的振动载荷，只有谐波频率为nNbΩ和(nNb±1)Ω的振动载荷能够通过桨毂传递到机身上，最终产生nNbΩ频率的桨毂振动载荷，被称为通过频率振动载荷，其中Ω为旋翼旋转频率，n取值范围为正整数。因此对于3片桨叶的旋翼，后缘襟翼控制频率通常选择2Ω,3Ω和4Ω，襟翼控制律可以傅里叶级数展开的形式表示为

(23)

为了研究后缘襟翼偏转的幅值、频率和相位对振动载荷的影响，首先进行了开环控制仿真研究，包括扫幅、扫频和扫相。在前进比为0.14时，2Ω,3Ω和4Ω频率控制下不同幅值控制输入在不同相位对3Ω垂向振动载荷幅值的影响分别如图6～图8所示。

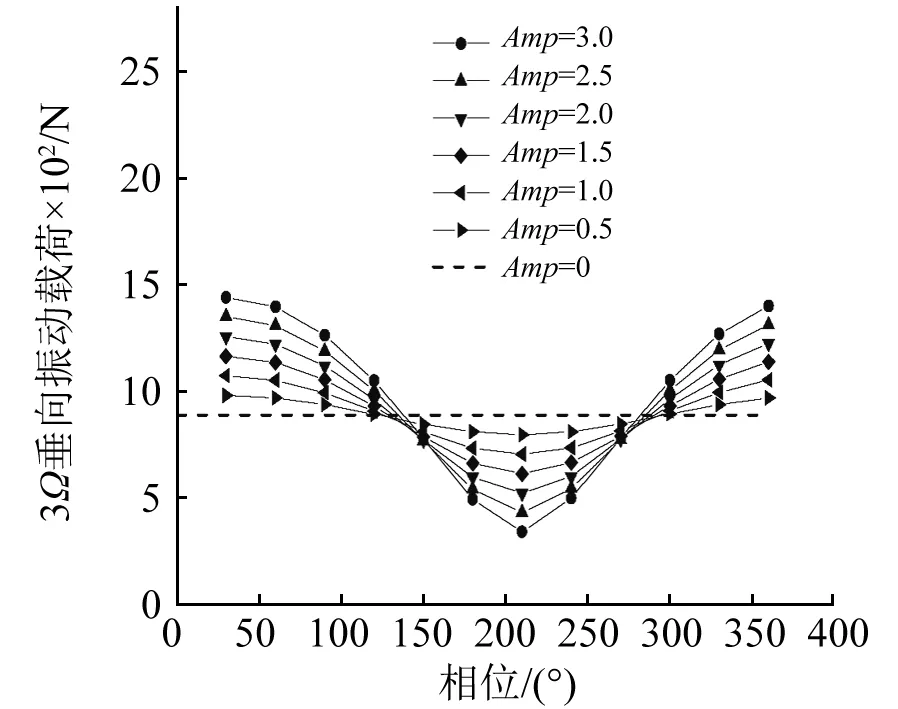
图6 2Ω控制输入不同幅值扫相结果(μ=0.14)Fig.6 Phase sweep results of different amplitudes for 2Ω control input(μ=0.14)

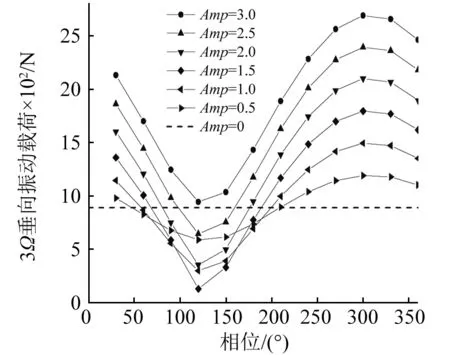
图7 3Ω控制输入不同幅值扫相结果(μ=0.14)Fig.7 Phase sweep results of different amplitudes for 3Ω control input(μ=0.14)

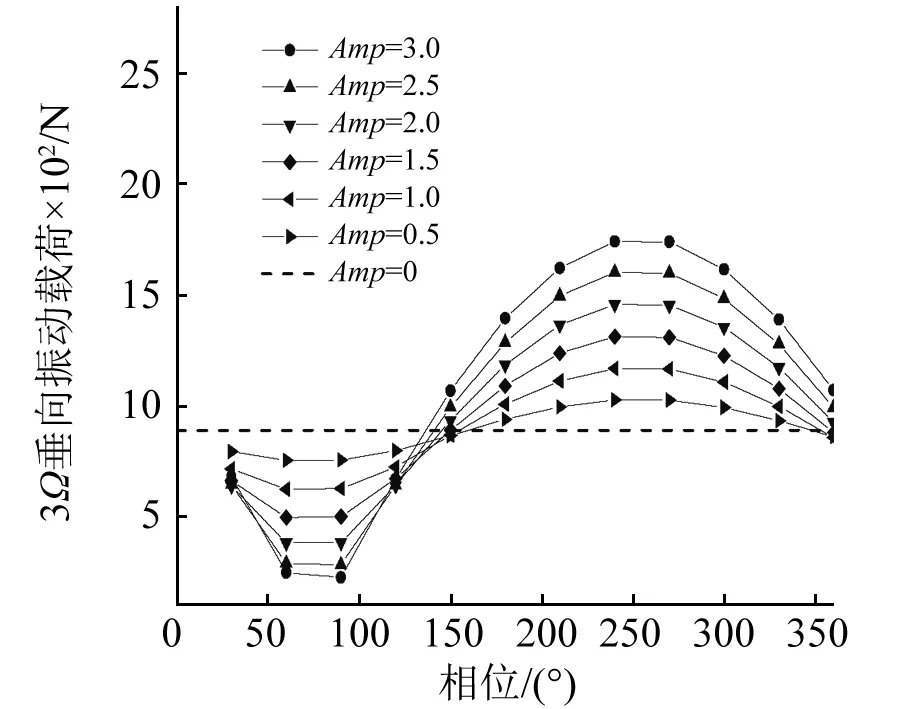
图8 4Ω控制输入不同幅值扫相结果(μ=0.14)Fig.8 Phase sweep results of different amplitudes for 4Ω control input(μ=0.14)

从图中可以看出，后缘襟翼以2Ω,3Ω和4Ω频率偏转均能够对3Ω垂向振动载荷幅值产生影响，影响的程度随襟翼偏转幅值的增大而增大，不同相位控制的效果存在差异，并且不同谐波控制输入的最佳相位也不相同。将桨毂振动载荷展成傅里叶级数的形式，设定后缘襟翼的偏转幅度为1.5°，不同的控制频率对振动载荷的余弦分量与正弦分量的影响如图9、图10所示。

对于本文以SA-349直升机旋翼为基础构建的智能旋翼模型，在相同的襟翼偏转幅值下，后缘襟翼不同的运动频率对不同方向振动载荷幅值的影响程度也有所不同，对于垂向的振动载荷，3Ω的控制效果最为显著， 而对于桨毂平面内的振动载荷，4Ω的控制效果略优于3Ω控制，2Ω控制输入的效果最弱。原因是对于3片桨叶的SA-349直升机旋翼，3Ω控制输入在桨叶上产生的nΩ谐波载荷中，3Ω谐波最为显著，根据桨毂载荷传递规律，对于作用在桨毂上的垂向载荷，只有nNbΩ谐波能够通过桨毂传递到机身上，同理对于桨毂平面内的振动载荷，4Ω的控制效果最明显。通常直升机桨叶扭转刚度较大，其一阶扭转频率要远大于旋转频率， SA-349旋翼桨叶在工作转速时一阶扭转频率在5Ω左右，根据桨叶振动响应的动力放大因素，激振频率越接近桨叶固有频率，响应幅值越大，因此4Ω激励引起的桨叶扭转响应要大于2Ω激振频率，其控制效果也更加明显。

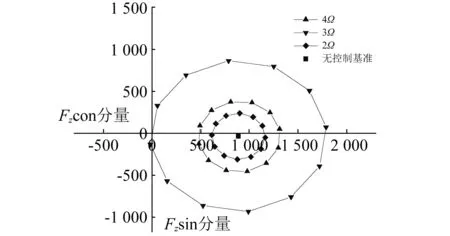
图9 不同控制频率对垂向振动载荷的影响Fig.9 Frequencies’ influence on vibratory load of vertical direction

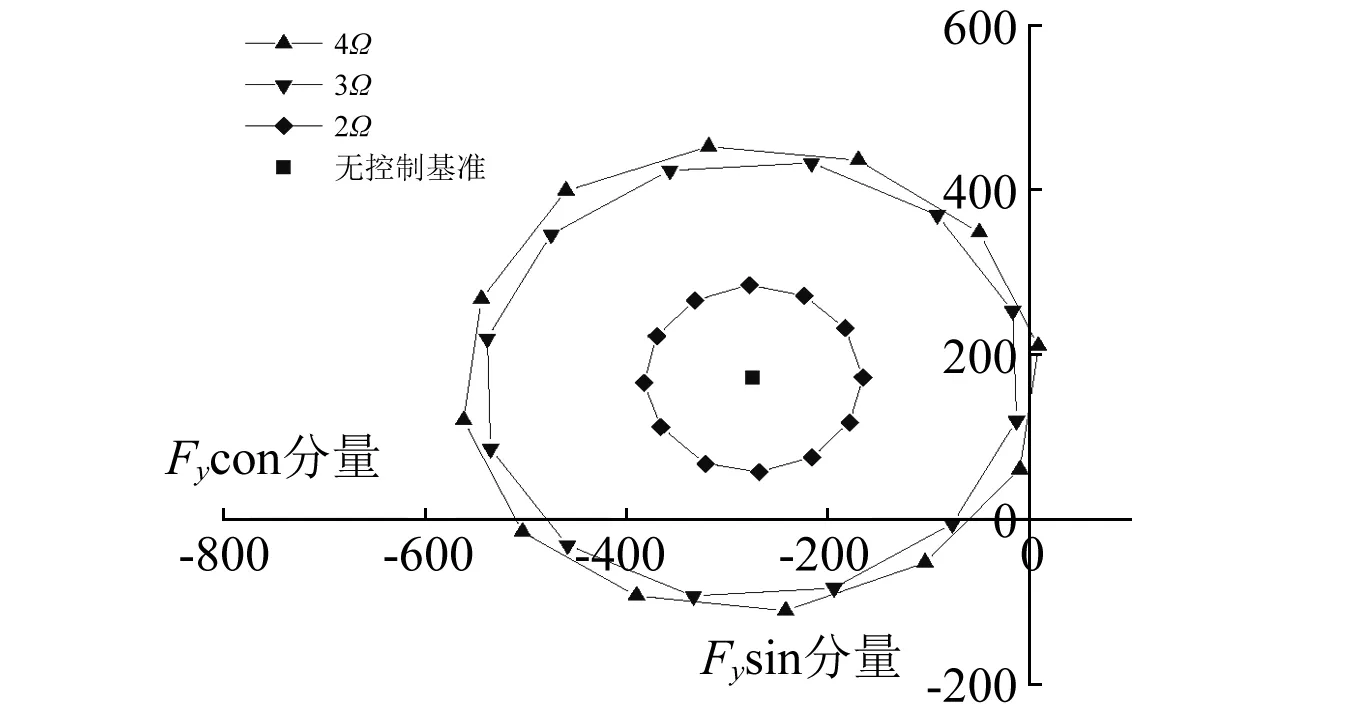
图10 不同控制频率对桨毂平面内振动载荷的影响Fig.10 Frequencies’ influence on in-plane vibratory load

3 振动闭环控制仿真

在后缘襟翼智能旋翼振动开环控制中，通过扫频、扫相和扫幅试验可以寻找到对于特定方向振动载荷抑制效果最为明显的控制规律，但是该方法过程繁琐，且难以同时兼顾多个方向的振动载荷。在实际的后缘襟翼智能旋翼试验中，通常采用闭环控制方法对振动载荷进行控制，控制系统如图11所示。

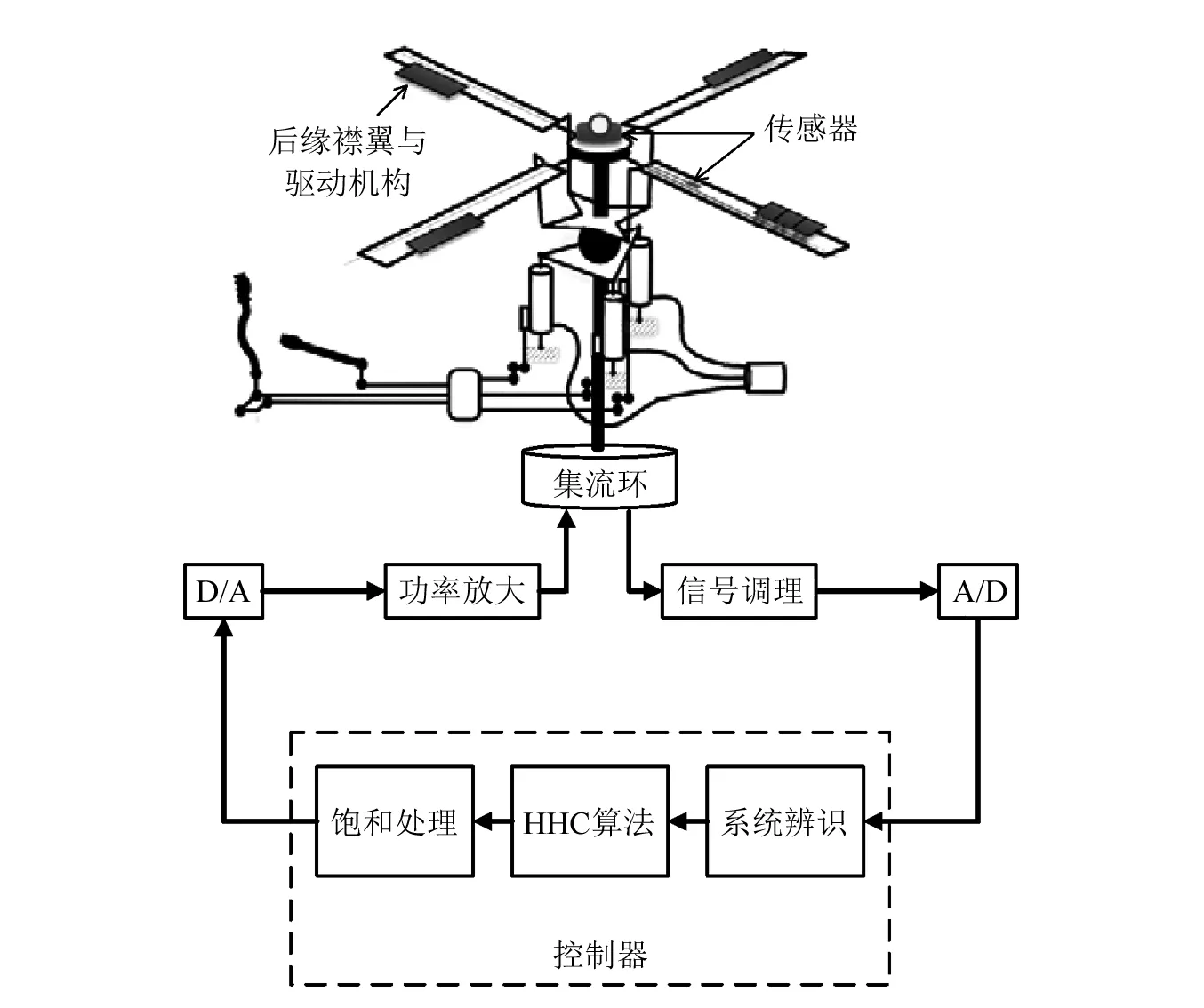
图11 智能旋翼闭环控制示意图Fig.11 Schematic of active rotor closed-loop control

分布在旋翼桨叶或桨毂上的传感器将旋翼振动载荷转换为电信号，通过信号调理和模数转换后传递到控制器中，控制器根据获得的振动载荷信息，分析计算得到当前状态下后缘襟翼最优控制律，再通过数模转换和功率放大后将驱动电压传递到后缘襟翼驱动机构，控制后缘襟翼主动偏转以实现对旋翼振动载荷抑制。

高阶谐波控制算法最早应用于控制自动倾斜器不动环的高阶谐波控制智能旋翼振动控制，该算法计算效率高、控制效果明显，被推广到包括主动控制拉杆、后缘襟翼式智能旋翼以及主动扭转旋翼控制中[11-13]。该算法假设直升机旋翼系统为线性定常系统，控制输入谐波θk(系统输入)和振动载荷谐波zk(系统输出)满足

zk=T·θk+Wc·w

(24)

式中：Wc·w为与直升机操纵相关量，而对于后缘襟翼无控情况下的系统输入和系统输出满足

z0=T·θ0+Wc·w

(25)

由式(24)与式(25)联立，得到

Δz=T·Δθ

(26)

式中：Δθ为系统输入的变化；Δz为系统输出的变化。从而有

(27)

定义振动控制目标函数为

(28)

式中:Q和R分别为系统输出和系统输入的权重值矩阵。当Q的值大于R时，表示目标函数用于寻找使得通过频率振动载荷幅值最小的控制律，而弱化控制输入的幅值的影响，反之则表示用于寻找控制输入最小时的最优控制律。通过开环控制仿真发现，后缘襟翼控制输入的幅值越大其控制效果越明显，此时后缘襟翼驱动机构的需用功率也就越大，适当降低后缘襟翼的控制输入幅值，可有效减小后缘襟翼的能量消耗。通过调整Q和R的值，可以在最小振动幅值和最小控制输入间取得平衡。对于本文所构建的智能旋翼控制模型，目标是降低各个方向的振动载荷分量，同时兼顾后缘襟翼的需用功率，因此Q和R的值设定为单位矩阵I。当目标函数值取极值时满足

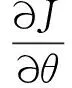
(29)

将式(24)和式(28)代入式(29)，整理得到最优控制律表示为

θopt=(TT·Q·T+R)-1·TT·Q·(T·θ0-z0)

(30)

在实际的智能旋翼试验中，通常采用系统辨识的方式获得系统传递矩阵T。本文选择加权最小二乘法辨识，在经过了n次测量后，系统的输入变化矩阵和输出变化矩阵表示为

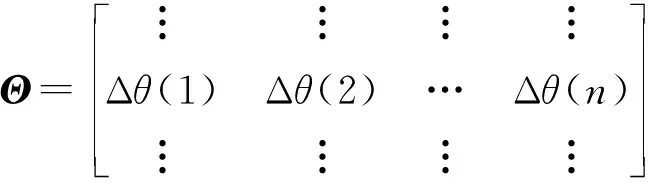
(31)

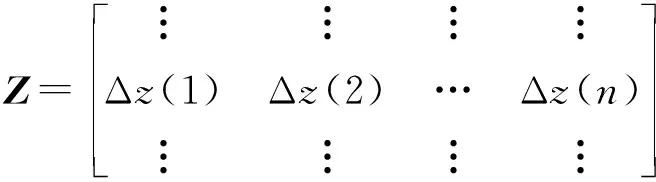
(32)

系统辨识的预测误差定义为测量值与预测值之间的偏差

εi=Zi-Ti·Θ

(33)

定义辨识的目标函数JI，辨识的目的就是寻找使得JI最小的系统传递矩阵T

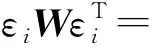
(Zi-Ti·Θ)W(Zi-Ti·Θ)T=

(34)

式中：W为权重值矩阵，表示每次测量的预测误差权重值。当直升机飞行状态发生突变时，系统的传递矩阵也会相应发生变化，在这种情况下突变后的测量值更能反映系统的当前状态，因此可以通过调整权重值矩阵W适当提高突变后预测误差的权重值。对于定常飞行状态，权重值矩阵可取单位矩阵。当目标函数取最小值时，应满足

(35)

从而得到传递矩阵T的第i行

Ti=ZiWΘT(ΘWΘT)-1

(36)

整个传递矩阵T

T=ZWΘT(ΘWΘT)-1

(37)

受制于当前作动器技术发展现状以及后缘襟翼机构设计水平，实际后缘襟翼偏转角度幅值受到一定的限制，而当式(28)振动控制目标函数中权重值设置不合理时，HHC算法计算得到的后缘襟翼偏角可能会超过襟翼机构最大偏转角度，此时后缘襟翼偏角不再随控制输入的增大而增大，从而产生驱动器饱和现象。这不仅会减弱智能旋翼振动控制效果，还可能造成驱动器损坏，因此需要对驱动器饱和状况进行处理[14-15]，本文采用自动调整权重值方法，通过调整式(28)中控制输入权重，调整后缘襟翼偏转角度，其调节过程如图12所示。

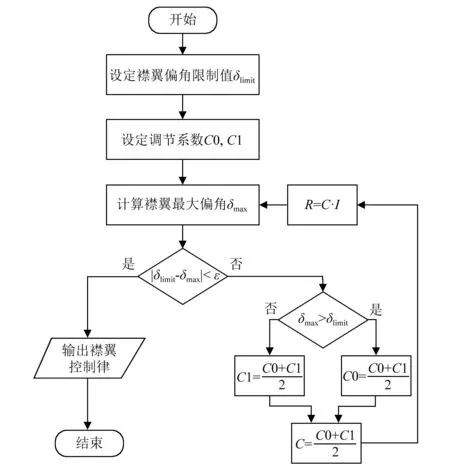
图12 驱动器饱和处理流程Fig.12 Processing flow of actuator saturation

本文针对前进比为0.14状态开展了闭环控制仿真研究，在参考国外智能旋翼试验基础上[16]，限定后缘襟翼偏角限制值为3°，不考虑测量误差的影响，利用所建立的控制方法获得的后缘襟翼最优控制律，如图13所示。

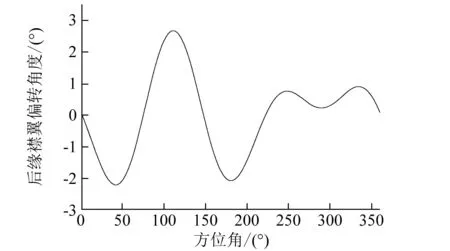
图13 后缘襟翼控制律Fig.13 Control law of the ACF

为便于比较各个方向振动载荷幅值的变化，以后缘襟翼无控(襟翼未作动)状态下垂向振动载荷幅值为基准，对振动载荷的各力分量进行无量纲化，而以后缘襟翼无控状态下垂向振动载荷幅值与旋翼半径的乘积为基准，对振动载荷的各力矩分量进行无量纲化。经过无量纲化处理后的旋翼通过频率振动载荷幅值变化，如图14所示。

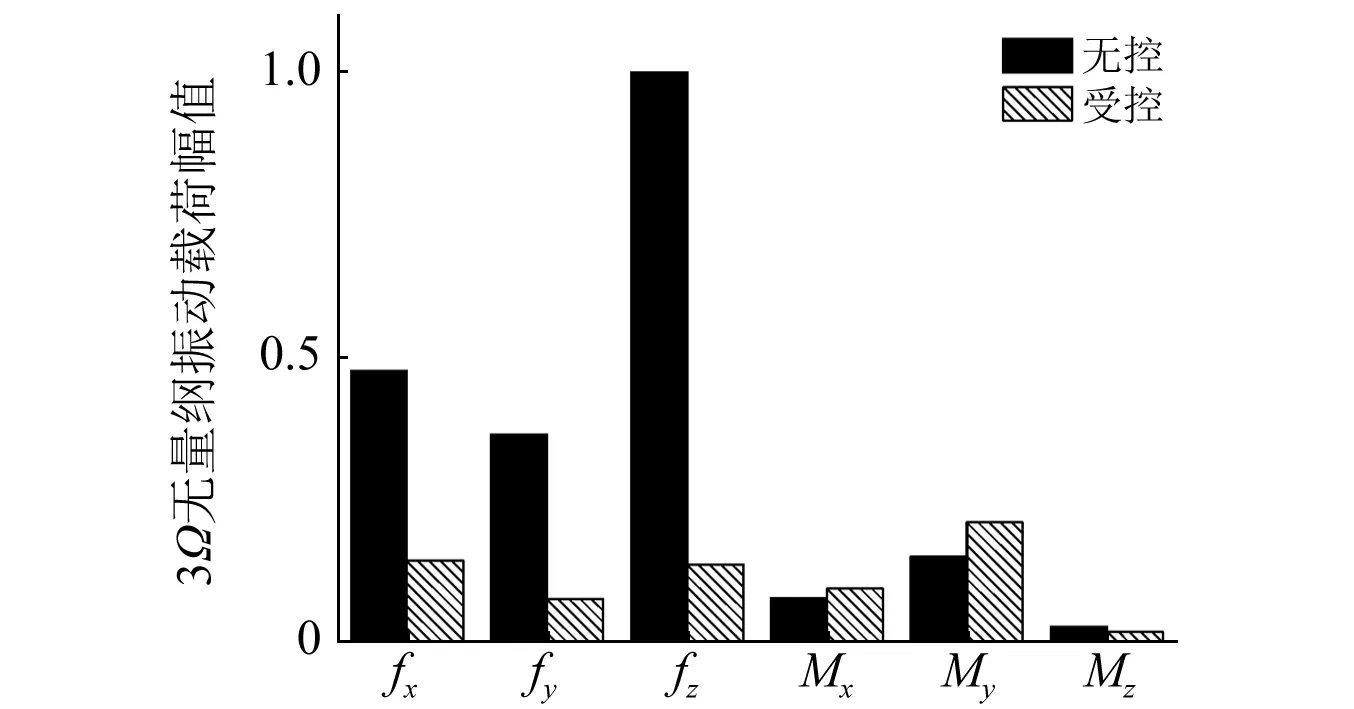
图14 旋翼振动载荷变化，无测量误差Fig.14 Variation in rotor vibratory loads, without measurement error

从图14中可以看出，除Mx和My振动载荷幅值略微增大外，其余方向振动载荷幅值均有明显的降低，其中Fz振动载荷幅值控制效果最为明显，减振幅度达到87%。

在实际试验中，对于系统输出zk的测量误差是真实存在的，测量误差的存在使得由式(37)计算得到的传递矩阵T与实际系统存在偏差，引入均匀分布的随机测量误差

ε=A·rand(nout,1)

(38)

式中：A为测量误差的幅值；nout为系统输出列向量的维数。在前进比为0.14时，桨毂3Ω振动载荷幅值最大值为900左右，引入幅值为500的测量误差，此时高阶谐波控制器的振动控制效果，如图15所示。

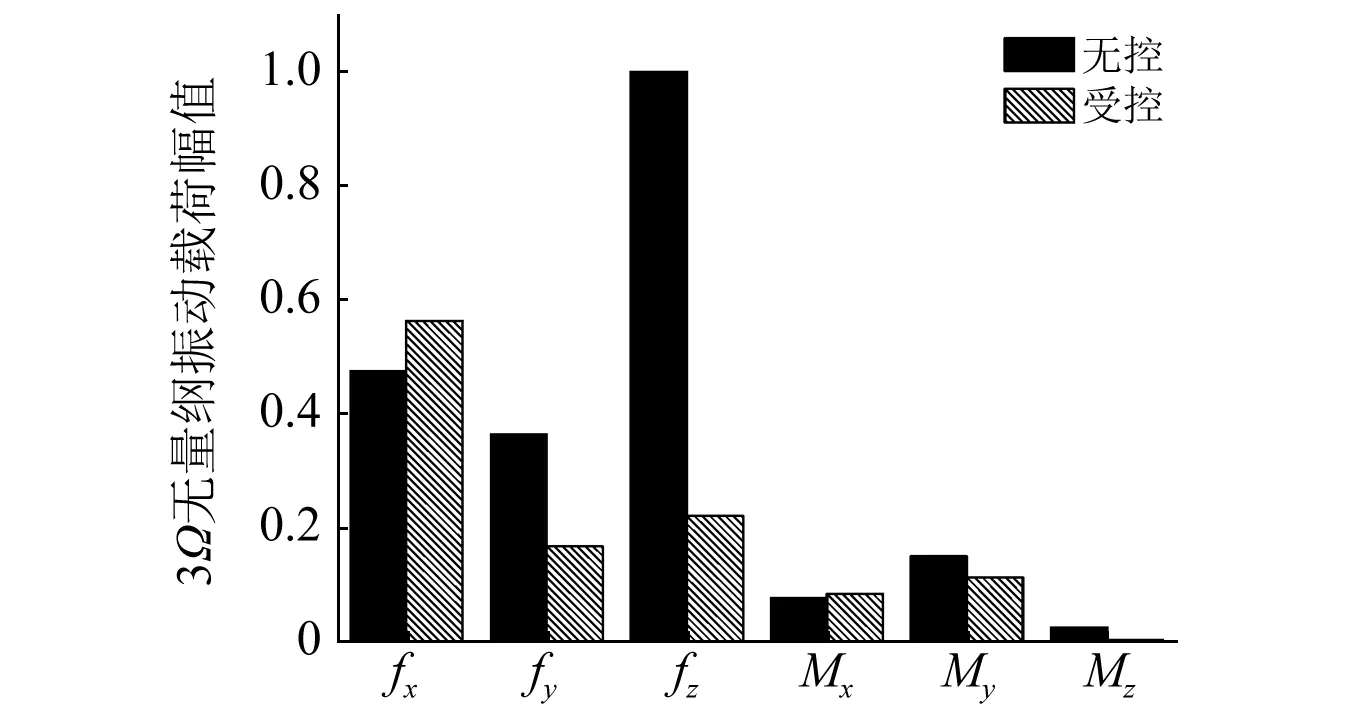
图15 旋翼振动载荷变化，误差幅值500Fig.15 Variation in rotor vibratory loads, with measurement error magnitude of 500

测量误差的引入在一定程度上削弱了高阶谐波控制器的振动控制能力，但是仍能良好的振动控制效果，垂向振动载荷幅值降低78%左右。增大测量误差幅值至1 000，此时测量误差值超过系统实际响应幅值，旋翼振动载荷幅值变化，如图16所示。

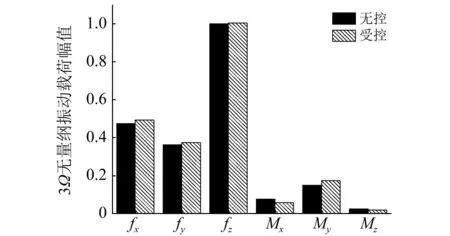
图16 旋翼振动载荷变化，误差幅值1 000Fig.16 Variation in rotor vibratory loads, with measurement error magnitude of 1 000

从图16可知，此时控制器已无明显控制效果，某些方向振动载荷幅值甚至有所增加。原因是测量误差使得辨识出的系统传递矩阵产生较大偏差，因此在实际智能旋翼试验时，还需要辅以其他措施以减小测量误差的影响。

4 结 论

利用建立的带后缘襟翼旋翼气弹耦合动力学模型，对后缘襟翼智能旋翼进行了控制仿真，采用高阶谐波控制算法结合加权最小二乘法辨识，开展了智能旋翼闭环控制仿真研究，获得了如下研究结论：

(1)后缘襟翼偏转运动能够显著影响旋翼通过频率振动载荷幅值，对于相同频率的襟翼偏转控制律，偏转幅值越大对振动载荷幅值的影响程度也越大，对于相同的襟翼偏转幅值，不同频率的襟翼控制律对振动载荷幅值的影响程度也不相同，振动载荷幅值最低时对应的最优控制相位也存在差异。

(2)采用高阶谐波控制算法的智能旋翼闭环控制虽然可能会引起个别方向振动载荷幅值的略微增加，但是能够对通过频率桨毂振动载荷产生良好的综合控制效果。

(3)采用加权最小二乘法辨识的智能旋翼闭环控制器对于测量误差表现出较强的鲁棒性，随测量误差幅值的增大，控制器振动控制效果虽然有所减弱，但在试验测量误差幅值不大于振动载荷真实幅值情况下，控制器仍具有较好的振动控制能力。