尺度各异刚体碎块断裂面的匹配方法
2019-02-22赵夫群周明全耿国华
赵夫群, 周明全, 耿国华
(1.西北大学 信息科学与技术学院,陕西,西安 710127;2.咸阳师范学院 教育科学学院,陕西,咸阳 712000;3.北京师范大学 信息科学与技术学院,北京 100875)
厚度不可忽略的刚体碎块的匹配可以通过对碎块断裂面的匹配来实现,即为两个不同坐标系下的断裂面寻找一个合适的变换,使得两个曲面能够完全配准或重合. 目前,曲面匹配方法已经在三维建模[1]、文物复原[2-3]、航空影像处理[4]以及医学研究[5]等领域得到了广泛的应用.
目前有很多刚体碎块断裂面的匹配方法,可以利用点特征进行匹配,如Pokrass 等[6]通过对碎块断裂面进行离散采样得到的若干采样点进行匹配;也可以利用断裂面的轮廓曲线特征进行匹配,如李群辉等[7]提出了一种基于轮廓曲线特征的刚体碎块断裂面匹配算法,王洋等[8]提出用傅里叶变换边缘曲线法来实现W型轮廓曲线的快速匹配方法;此外还可以利用区域特征进行匹配[9],如Papaioannou等[10]通过获取断裂面上的局部特征区域实现了碎块的匹配. 以上这些算法都在一定程度上实现了刚体碎块的匹配问题,但是它们大多只考虑匹配中的刚体变换问题,在实际的匹配应用中往往还存在着尺度因素.
本文充分考虑尺度因素,针对刚体碎块的三角网格数据模型,采用一种改进的ICP算法进行碎块的匹配,即在ICP算法中添加尺度矩阵、旋转角约束和动态迭代系数,来解决碎块的尺度匹配问题、因刚体变换中旋转角变换过大引起的匹配失败的问题以及匹配速度的问题.
1 断裂面的提取
为了提高计算速度、减少存储空间、突出建模特征,首先采用基于平均曲率的精简算法[11]对初始数据模型进行精简. 然后进行碎块外面表面的分割,即将碎块的外表面以棱边为界限分割成多张曲面. 这里采用区域生长算法[12]实现曲面分割,具体思想为:首先判断相邻三角面片法矢的夹角是否大于给定阈值,若大于给定阈值则将这两个三角面片分割在两个不同的曲面上,否则分割在同一曲面上,重复该过程直到所有三角面片分割完成为止;然后逐一检查分割曲面,若曲面特别小,则将其合并到相邻的曲面中,否则判断该曲面与其相邻曲面的平均法矢夹角,若小于给定阈值则进行合并,否则不合并.
针对刚体碎块的断裂面较原始面更加粗糙的情况,可以根据断裂面上所有顶点的法向量的变化情况来区分断裂面和原始面,表现在几何特征上就是断裂面上顶点的法向量变化较大.
定义曲面φ上顶点p的弯能量ek(p)为
(1)
式中:qj表示顶点p在曲面φ上k近邻的顶点;np和nqj分别表示p和qj的法向量.
设置一个以p为球心r为半径的包围球,则点p在邻域Br(p)内的局部弯曲能力定义为
(2)
式中:Nr(p)=Br(p)∩φ.
那么,曲面φ的平均粗糙度为
(3)
若ρ(φ)大于给定阈值ρ′,则认为该曲面为断裂面,否则认为该曲面为原始面.
2 断裂面的匹配
2.1 ICP算法
设两个待匹配的断裂面为φ1和φ2,其三角网格数据模型所对应的三维点集分别为D={di}和M={mj},i=1,2,…,Nd,j=1,2,…,Nm,Nd和Nm分别表示点集D和M的大小. 那么断裂面φ1和φ2的匹配问题实际上就是点集D和M的配准问题,即寻找变换T使得D和M能够最佳匹配,可以采用最小二乘(least square,LS)法计算,计算式为
(4)
由Besl等[13]提出的ICP算法解决的就是两个点集的配准问题,即寻找从点集D到M的旋转和平移变换,使得它们能够达到最佳配准,即令式 (4) 中的T为刚体变换(包括旋转和平移变换),计算式为
s.t.RR=Im,det(R)=1.
(5)
式中:R表示旋转矩阵;t表示平移变换.
ICP算法的具体实现步骤如下.
① 建立点集D和M的相关性,计算式为
(6)
式中i=1,2,…,Nd.
② 计算点集D和M的新旋转和平移变换,计算式为
(R*,t*)=
(7)
然后,更新Rk+1和tk+1,计算式为
(8)
重复步骤①和②,直到满足终止条件为止.
虽然ICP算法是一种精度较高的点集配准算法,但是它没有考虑尺度因素. 在实际应用中,经常要考虑尺度配准的问题,也就是既有尺度变换又有刚体变换的情况.
2.2 SICP算法
既有尺度变换又有刚体变换的点集配准可描述为[14]
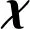
(9)
式中:S=diag[s1s2…sm]为一个尺度矩阵;R为一个正交矩阵;t为一个平移矢量.
将式 (9) 代入到式 (4) 中,则有
(10)
那么式 (10) 就描述了尺度配准问题,式中正交矩阵R表示旋转变换. 为了避免一个点集收敛到另外一个点集中的一个很小的子集情况,也就是尺度矩阵为0矩阵的情况,就必须为尺度矩阵S设置边界. 于是,该尺度配准问题又进一步转换为
(11)
式中:S为一个带有边界的尺度矩阵;R为一个旋转矩阵;t为一个平移矢量.
那么SICP算法的实现步骤如下.
① 通过当前的变换 (Sk,Rk,tk)建立点集D和M的相关性,计算式为
(12)
② 令S=diag[s1s2…sm],计算新的变换(Sk+1,Rk+1,tk+1),计算式为
(Sk+1,Rk+1,tk+1)=
(13)
重复步骤①到②,如果S的变化量 ΔS=|Sk+1-Sk|小于阈值ε或达到最大迭代次数εmax,则停止该迭代过程.
2.3 改进的ICP算法
为了进一步提高SICP算法的配准精度和收敛速度,首先在SICP算法中引入旋转角约束(即设置旋转角的上界和下界),解决由旋转角变化过大引起的配准失败的问题,然后加入动态迭代系数h,以提高算法的收敛速度. 这里将这种改进的SICP算法简称为改进的ICP算法.
首先,针对两个3D点集的配准问题,定义旋转矩阵R为R=RxRyRz.Rx,Ry,Rz分别为
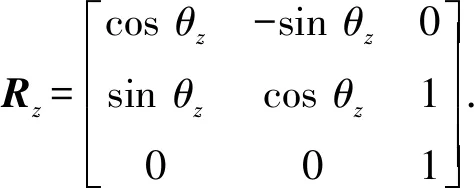
式中:θx、θy和θz为旋转角[15];θxb、θyb和θzb表示旋转角的均值;Δθx、Δθy和Δθz为旋转角的偏差;θxb-Δθx、θyb-Δθy和θzb-Δθz为旋转角的下界;θxb+Δθx、θyb+Δθy和θzb+Δθz为旋转角的上界.
旋转角的主成分矢量采用主成分分析(princilalcomponentanalysis,PCA)方法来计算. 对于3D点集的刚体配准,如果这两个点集能够正确配准,那它们必然具有相似的点分布. 因此当它们正确配准时,旋转角的3对主成分矢量都接近0°或180°. 所以旋转角可以通过旋转角的3对主成分矢量来估计.
假设点集D和M的主成分分别为:VD={VD1,VD2,VD3}和VM={VM1,VM2,VM3},VDi和VMi是3×1的矢量,i=1,2,3. 那么点集M中有8组主成分满足条件,即
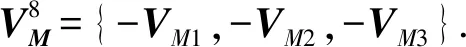
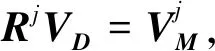
(14)
旋转角的均值θxb、θyb和θzb可以通过式(14)的计算得到. 旋转角的偏差Δθx、Δθy和Δθz的值取决于点集的相似程度,具体由实验情况来给定,为了计算方便可以设置为Δθx=Δθy=Δθz=10°.
那么点集D和M的配准问题可进一步描述为
动态迭代系数h是一个可以自动调整变换参数的整数值,它可以在不影响算法的配准精度和收敛方向的情况下,大大减少算法的迭代次数、提高算法的收敛速度. 在SICP算法中加入动态迭代系数h的步骤如下:
① 计算刚体变换矢量q=[Rk|tk]T以及qk的相邻两次迭代的变化量Δqk;
② 用刚体变换矢量Δqk更新SICP算法步骤2)中的(Sk+1,Rk+1,tk+1)共h次,通常h是一个大于等于0的整数.
那么改进的ICP算法的具体实现步骤如下.
① 给定刚体变换初值q=[R0t0]T,R0为初始旋转矩阵,t0为初始平移矢量,初始尺度值为S0,尺度的边界为[ak,bk];
② 令D0=R0S0D+t0,迭代次数k=0,动态迭代系数h=0;
③k=k+1;
④ 估计旋转角度θx,θy,θz的边界,即θx∈[θxb-Δθx,θxb+Δθx],θy∈[θyb-Δθy,θyb+Δθy],θz∈[θzb-Δθz,θzb+Δθz],Δθx=Δθy=Δθz=10°;
⑤ 计算最优旋转角θxo,θyo,θzo,最优旋转矩阵Ropt=RxoRyoRzo;
⑥ 利用式 (12) 建立点集D和M的相关性ck(i)∈{1,2,…,ND};
⑦ 利用奇异值分解法计算旋转矩阵Rk、平移矢量tk和尺度Sk;
⑧ 计算Dk=RkSkD+tk及其相邻两次迭代的变化量ΔDk;
⑨ 判断动态迭代系数h,若h>0,则利用式 (15) 计算新的变换(Sk+1,Rk+1,tk+1),并执行Δqk(Sk+1,Rk+1,tk+1)共h次来进一步更新变换;
⑩ 判断均方根误差σRMS,若σRMS,k+1-σRMS,k>ε,则执行h=h+1操作,否则执行h=0操作,RMS的定义为
.
(16)
3 碎块匹配实验
实验采用公共数据集石头和灰泥碎块[16]以及3D扫描仪获取的兵马俑碎块完成匹配,所有碎块均采用三角网格数据模型表示,如图1所示,显然匹配中存在尺度变换. 匹配过程为:首先提取碎块的断裂面,然后分别采用ICP算法、SICP算法和改进的ICP算法对碎块断裂面进行尺度配准. 石头碎块、灰泥碎块和兵马俑碎块的匹配结果分别如图2、图3和图4所示.
从图2、图3和图4的匹配结果来看,ICP算法不能实现碎块的尺度匹配,而SICP算法和改进ICP算法均能实现碎块的尺度匹配,并且改进ICP算法的匹配误差更小,效果更好. 实验中,ICP算法、

图1 待匹配的碎块 Fig.1 Blocks needed to be matched
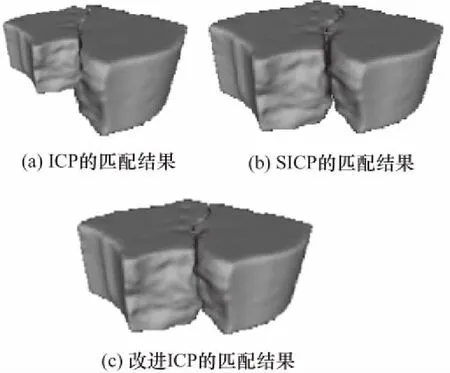
图2 石头碎块的匹配结果Fig.2 Matching results of stone blocks
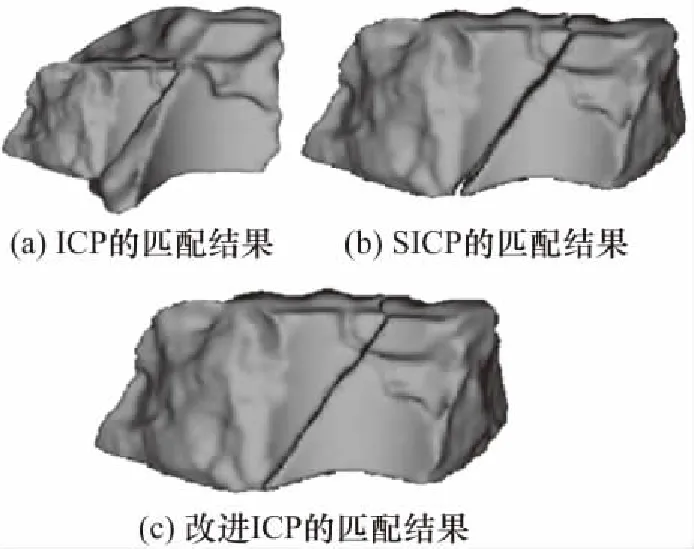
图3 灰泥碎块的匹配结果Fig.3 Matching results of plaster blocks
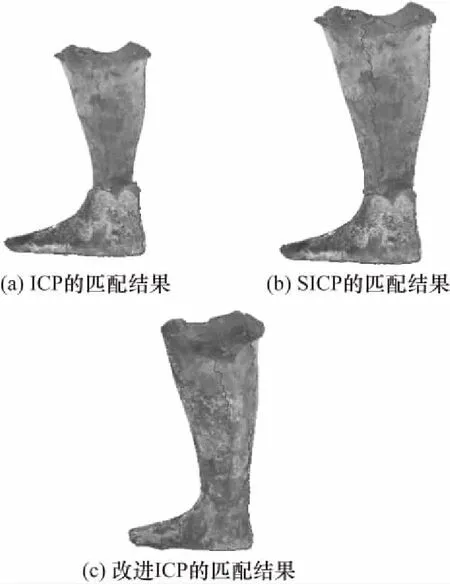
图4 兵马俑碎块的匹配结果Fig.4 Matching results of Terracotta Warriors blocks
SICP算法和改进ICP算法的匹配参数(匹配误差、迭代次数和耗时等)如表1所示.

表1 算法的匹配参数
从表1可见,ICP算法的匹配误差较大,SICP算法和改进ICP算法均有较高的匹配精度,并且改进ICP算法的匹配速度和精度较SICP算法又有了大幅度的提高,是一种精度更高、收敛速度更快的碎块断裂面点集匹配算法.
4 结束语
针对厚度不可忽略的刚体碎块的三角网格数据模型,本文提出了一种改进的ICP算法来对两个刚体碎块的断裂面进行精确匹配. 该算法通过加入尺度矩阵、旋转角度约束和动态迭代系数的方式来改进ICP算法,使得算法在匹配精度、速度等方面的性能都得到了很大的提高,能够将两个不同尺度碎块的断裂面进行精确、快速地对齐. 在今后的研究中,要进一步考虑噪声和外点对碎块匹配精度和速度的影响,提出更加精确、快速和抗噪的碎块匹配算法. 此外,还要进一步研究特殊碎块的匹配问题,如兵马俑碎块,分析其特点,寻找更加适合这种特殊复杂碎块的匹配算法,以达到自动虚拟复原兵马俑的目的.
