欧拉刚体旋转定理虚拟实验设计*
2021-07-21崔玉鑫杨彬杨洋王超飞
◆崔玉鑫 杨彬 杨洋 王超飞
0 前言
欧拉旋转定理[1]是由瑞士著名数学家和物理学家莱昂哈德·欧拉提出的:刚体绕定点的任意有限转动可由绕过该点某根轴的一次有限转动实现。可理解为刚体从一个姿态运动到任意一个姿态可由绕某根轴一次转动某个角度实现。该轴称为欧拉一次转轴,该角称为欧拉一次转角。
欧拉旋转定理是刚体运动学中非常经典的定理之一,其研究意义在于:一方面,它是转动四元数和欧拉四元数姿态坐标的理论依据;另一方面,该定理蕴含了刚体姿态问题的几乎所有内容,理解了该定理也就弄清了刚体姿态问题的实质。但由于欧拉旋转定理非常抽象[2-3],在三维空间一般很难找到欧拉一次转轴和欧拉一次转角,必须经过复杂的计算才能获得,即使这样也很难想象绕欧拉一次转轴转动欧拉一次转角后,刚体能够转到什么姿态,使得学生学习起来很困难。为此,本文借助国家级虚拟仿真实验教学中心——机械虚拟仿真实验教学中心的建设机会,设计一套证明欧拉旋转定理的虚拟实验台。
1 实验台总体结构与实验原理
实验台结构与作用 如图1所示,该实验台由两个装置组成,即装置一和装置二。
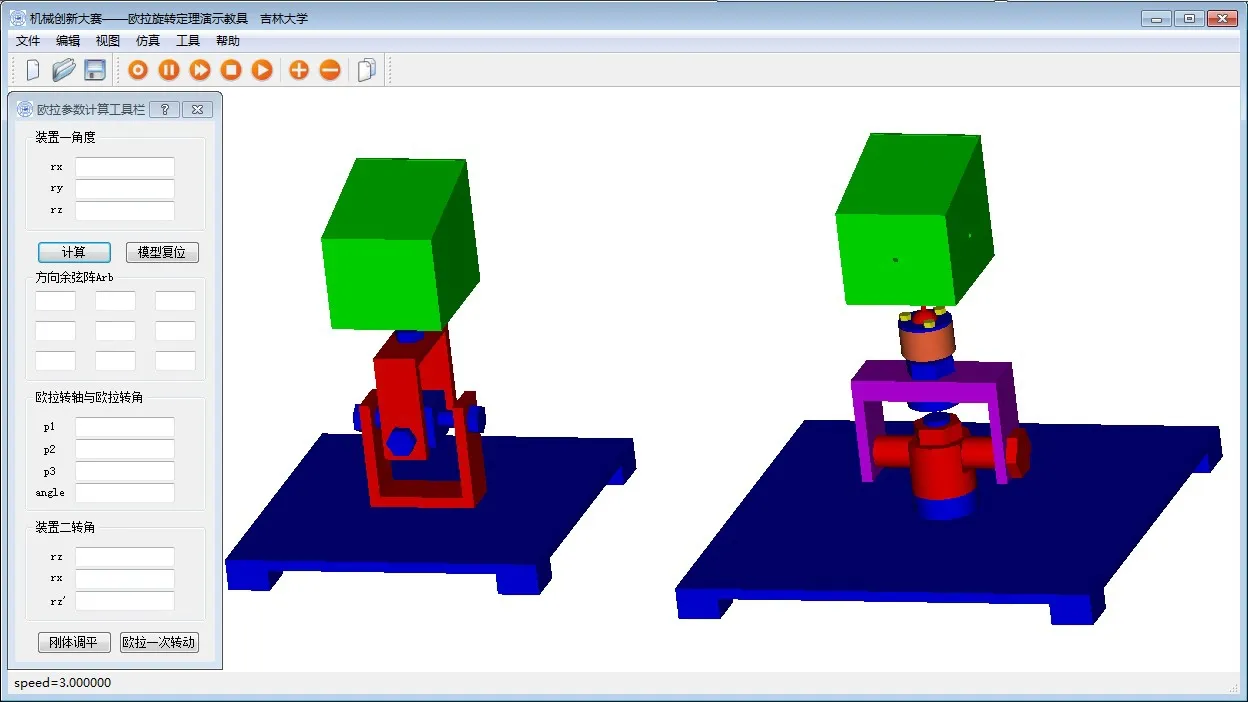
图1 欧拉旋转定理虚拟实验台视图
装置一的作用是设定刚体在空间中某一任意姿态。上端的类似长方体的物体代表刚体,下端为支座,刚体与下端支座之间通过一个万向节和一个转动铰相连,使得刚体与支座之间有三个相对自由度,从而能够达到有限范围内的任意姿态。
装置二的作用是通过测量和计算得到的装置一中刚体转动的欧拉一次转轴和欧拉一次转角来重现装置一中刚体的姿态,从而达到欧拉旋转定理的演示目的,同时证明欧拉旋转定理的正确性。装置二的上端是一个与装置一中相同的刚体,下端为支座,与支座相连的为一绕z轴转动的转动铰,设转角为H;与这个转动铰相连的是一个绕x轴转动的转动铰,设转角为p,利用这两个转动铰可确定欧拉一次转轴p。与刚体相连的是一个球铰,其作用是将刚体调整回初始姿态,原因是:在确定欧拉一次转轴过程中进行两次转动,刚体也随之转动,使得确定欧拉轴之后刚体的姿态不在初始姿态,而装置一中的刚体姿态是从初始姿态开始变化的。为了实现姿态的复现,完成欧拉一次转动,则装置二中的刚体也要由初始姿态开始转动。球铰的下边是一个转动铰(欧拉一次转动铰),当利用与支座相连的两个转动确定了欧拉一次转轴之后,欧拉一次转铰的轴线方向即为该方向。将刚体调整回初始姿态并锁死球铰后,便可以利用欧拉一次转动铰转过欧拉一次转角θ来实现欧拉旋转定理的演示。
实验原理 设在装置一中,通过其上的刻度尺读出的各个转动的角度分别是φ1,φ2,φ3,利用这三个角度可以计算出刚体所处的姿态,即方向余弦阵:
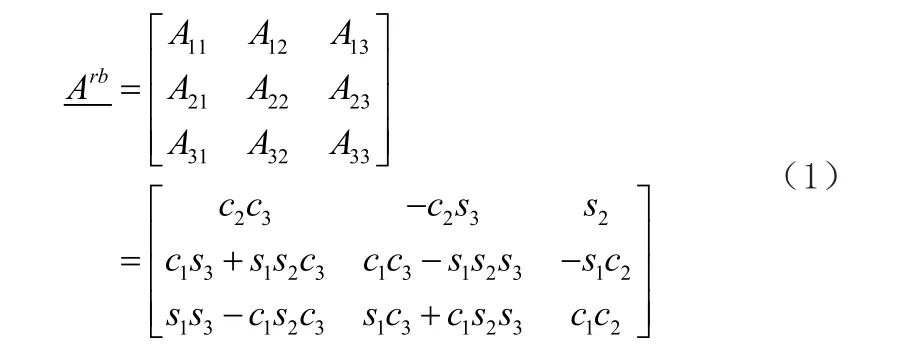
其中,s1=sinφ1,c1=cosφ1,其余类似。
欧拉一次转轴和欧拉一次转角的计算方法如下。
1)利用解线性方程组的高斯消去法计算方向余弦阵对应于特征值为1的特征向量,并进行单位化处理,得到欧拉一次转轴p1、p2、p3。
2)根据式(2)计算cθ:

3)找出最大的pi,设其为pm,将其带入式(3)中的一式可求出sθ:
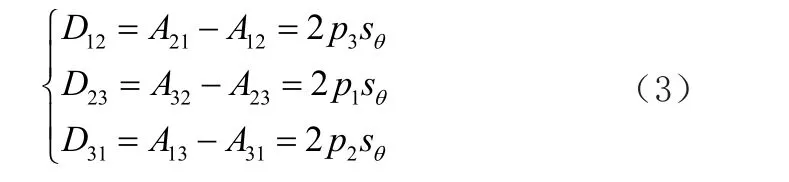
4)根据sθ和cθ,利用计算机语言的数学函数θ=atan2(sθ,cθ),便可计算出欧拉一次转角。
装置二中的转角为H和P的计算方法见式(4)。
2 虚拟实验
如图2所示,设装置一的刚体被搬动到该位置,各转轴处转角分别为10°、20°、30°,则计算得到的方向余弦阵见式(5)。

图2 装置一刚体运动到任意姿态

然后将装置二中的刚体转回初始姿态,如图3所示,并将球铰锁定。
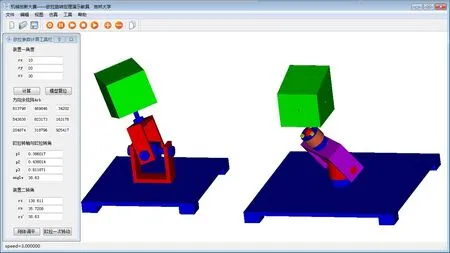
图3 装置二刚体运动到任意姿态
最后将装置二中的刚体绕球铰下面的转动铰转动欧拉一次转角,即完成欧拉一次转动,刚体从初始姿态转动到装置一中刚体的姿态,如图4所示,从而证明欧拉旋转定理。
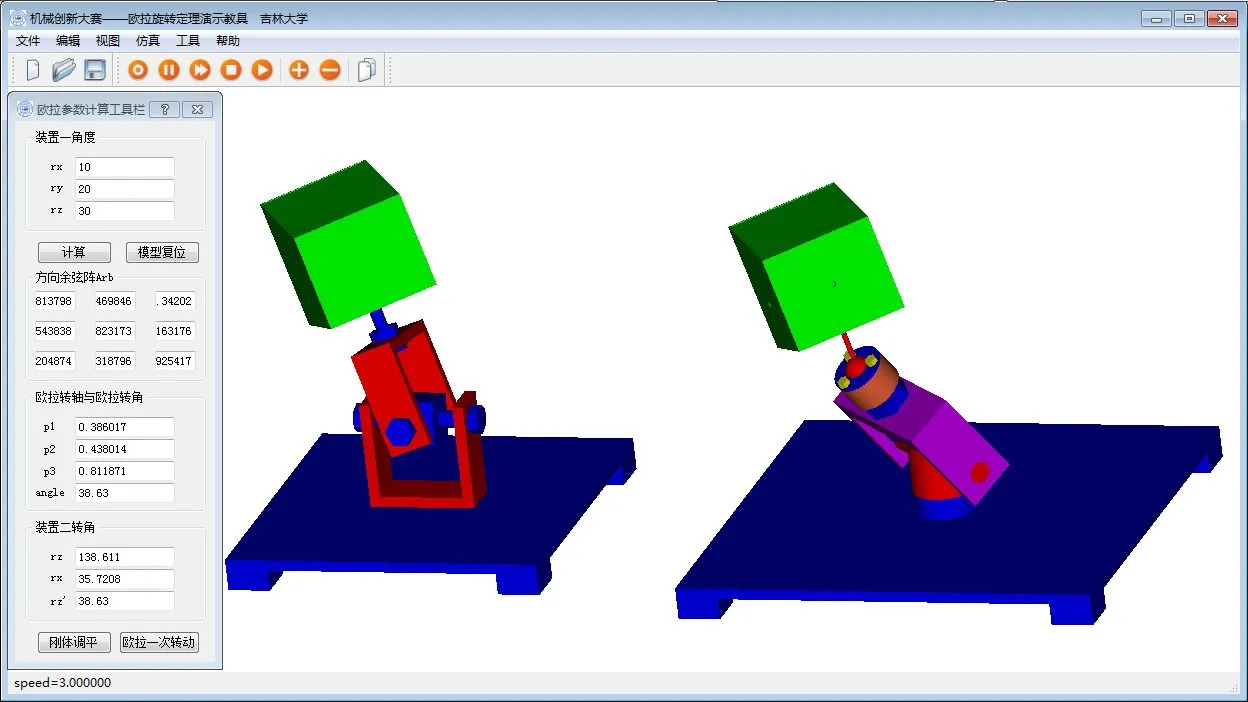
图4 装置二刚体进行欧拉一次转动后与装置一姿态相同
3 结语
针对刚体运动学相关课程教学过程中的欧拉旋转定理难以讲授、不易理解的问题,本文设计一套证明该定理的虚拟实验台,分析实验原理、实验步骤以及相应参数的解算方法,通过实例说明、证明虚拟实验的有效性。实验改革措施经笔者三年多的实践,效果较为令人满意。
