湿式铜基摩擦副局部接触对摩擦因数的影响

2019-02-22李明阳马彪李和言赵二辉杜秋李慧珠

北京理工大学学报 2019年1期

李明阳，马彪,2，李和言,2，赵二辉，杜秋，李慧珠

(1.北京理工大学机械与车辆学院，北京 100081；2.北京电动车辆协同创新中心，北京 100081)

铜基摩擦副为湿式离合器的关键组件，广泛应用于重型车辆，其性能优劣直接制约着传动系统的安全性和可靠性[1]. 工作中，离合器摩擦元件传递较大转矩的同时承受较高热负荷，极易发生屈曲变形，致使摩擦元件间发生局部接触. 当摩擦副所受载荷较大，接触表面一部分微凸峰因压力较大导致边界膜破裂，发生两表面直接接触，润滑状态由混合润滑向边界润滑转变. 边界润滑是由液体摩擦过渡到干摩擦过程之前的状态，是不光滑表面发生部分表面接触的润滑状况. 由于工程实际中多种不同类型润滑机理同时存在，且受到金属表面特性、润滑油中的微量成分、介质条件的影响，目前尚无统一的边界润滑理论，边界润滑的应用也还处于经验阶段. 杨本杰等[2]通过实验对不同形貌接触界面摩擦行为进行了研究，研究表明摩滑速度和接触压力是影响接触界面摩擦行为的重要因素. 赵二辉等[3-4]通过大量铜基摩擦副销-盘实验深入研究了温度、摩滑速度和接触压力对摩擦因数的影响，通过数据拟合得到了混合润滑状态下摩擦因数的表达式. 现有的研究表明，机械转矩和热应力引起的屈曲变形是导致摩擦元件间发生局部接触的主要原因. Xiong等[5]应用Timoshenko弯梁理论对摩擦元件的热屈曲问题进行了研究，并通过台架实验对模型进行了验证，研究表明，当周向热应力引起的周向弯矩超过摩擦元件的屈曲临界弯矩时，摩擦元件会发生屈曲变形. 李明阳等[6]建立了多片离合器摩擦元件临界屈曲弯矩计算模型，对机械转矩作用下摩擦元件周向屈曲变形问题进行了研究，并通过周向温度测量实验对屈曲模型进行了验证，研究表明，在较大机械转矩作用下，多片离合器摩擦元件间极易出现屈曲导致的局部高压接触. 李和言等[7]建立了摩擦热流密度与真实接触面积的动态分析模型，研究表明高热流密度输入条件下配对摩擦副真实接触面积仅为名义接触面积的10%～40%，即局部接触压力为名义平均压力的2.5～10倍. Zhao等[8]建立了局部接触下温度场计算模型，由温度仿真结果可知，在文献[7]中的接触比条件下，局部接触区压力集中，较短的摩滑时间即出现较高温度.

当前湿式铜基摩擦副摩擦因数研究中多采用宏观全接触模型，较少考虑摩擦元件屈曲变形导致的局部接触. 针对这一问题，本文建立了铜基摩擦副局部接触摩擦因数计算模型，对湿式离合器摩擦元件局部接触状态下，摩擦因数随摩滑过程发生变化的问题进行了研究.

1 局部接触摩擦因数计算模型

多片离合器中，对偶钢片发生周向屈曲变形后，摩擦元件间实际接触面积减小，接触区比压增大，在较大压力作用下，接触区表面微凸峰间接触更加充分，其中一部分微凸峰间的边界膜破裂，发生金属与金属接触，润滑状态逐渐转变为边界润滑为主的混合润滑状态. 摩滑过程中，局部接触通常引起较大的局部温升导致润滑油膜失效，此时摩擦状态由混合润滑转变为干摩擦. 滑摩结束后，在摩擦元件表面留下局部接触导致的摩擦磨损痕迹.

对于混合润滑状态的摩擦因数f，Bowden和Tabor提出其与边界膜的摩擦因数fl和干摩擦因数fc的关系为

f=α(T,Us)fc+[1-α(T,Us)]fl，

(1)

式中α为相对油膜亏量，是温度T和滑动速度Us的函数，可通过式(2)进行计算.

(2)

式中:tx为摩擦表面以滑动速度us通过接触长度x的时间，tx=x/us；tr为吸附分子占接触面的平均时间；ε为吸附热；R为气体常数；Ts为表面接触温度；M为润滑油摩尔质量；V为摩尔体积;Tcr为润滑油临界温度，即摩擦元件表面出现擦伤时的绝对温度. 由式(1)～(2)可知，相对油膜亏量α与温度正相关，与滑动速度负相关,摩擦因数与相对油膜亏量正相关.

传统以边界润滑为主的混合润滑摩擦因数计算时，常认为式(1)中干摩擦因数fc与边界膜的摩擦因数fl为定值. 文献[3]中大量的摩擦因数测量实验表明，fc为温度相关函数，fl为温度和压力相关函数，因此，式(1)可修正为

f(T,us,p)=α(T,us)fc(T)+[1-α(T,us)]fl(T,p)，

(3)

式中：fc(T)为干摩擦因数随温度变化函数；fl(T,p)为边界膜的摩擦因数随温度和压力变化函数.

文中考虑了热衰退对摩擦因数的影响，通过实验数据拟合的方式得到了干摩擦因数fc(T)的表达式(4)，拟合曲线如图1所示. 销-盘摩擦因数测量实验中，摩擦盘为铜基粉末冶金材料(95-5)，柱销材料为65Mn，摩擦因数拟合公式(4)适用于该摩擦副材料的干摩擦因数计算.

图1 干摩擦因数拟合曲线Fig.1 Friction coefficient fitting curve

fc(T)=5.11×10-10T3-3.017×10-6T2+

0.0015T+0.132，

(4)

式中T为局部接触区温度.

式(5)为考虑润滑油黏温、黏压特性应用Reynoleds公式得到的边界膜的摩擦因数表达式[4]. 本文仿真计算中选用的润滑油型号为RP-4652D，为实际车用传动润滑油，黏度等级为SAE 15W-40，质量等级为API CF-4. 压力p为3.5 MPa时，fl(T,p)随温度变化曲线如图2所示.

图2 边界膜摩擦因数曲线Fig.2 Boundary film friction coefficient

fl(T,p)=0.04exp[0.85×10-8p-0.03(T-T0)],

(5)

式中：T为局部接触区温度;T0为初始温度;p为局部接触区的平均面压.

由式(3)～(5)可知，摩擦因数是温度、压力和摩滑速度的函数，在铜基摩擦副摩滑过程中实时发生变化.

为了对铜基摩擦副局部接触摩擦因数计算模型的准确性进行验证，本文进行了销-盘摩擦因数测量实验. 实验设备采用UMT-3高温摩擦磨损实验机.该实验机包含湿式和干式两个模块，通过模块的更换可实现不同润滑状态下摩擦因数的测量. 图3所示的销-盘实验中，柱销材料为65Mn，摩擦盘摩擦层材料为铜基粉末冶金，具体实验工况如表1所示.

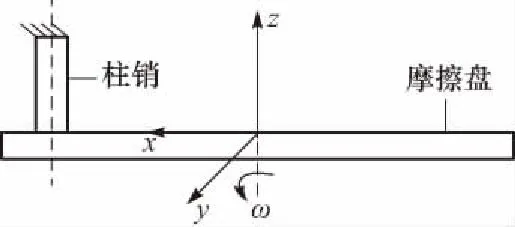
图3 销-盘摩擦因数测量实验Fig.3 Pin on disc tests

表1 实验工况参数Tab. 1 Experimental parameters

图4为不同实验工况下销-盘摩擦因数测量数据.

图4 摩擦因数测量结果Fig.4 Experimental results of friction coefficient

应用式(3)～(5)及表1和表2所示的参数进行摩擦因数仿真计算，将销-盘实验测得的摩擦因数与仿真计算结果列入表3进行对比分析.

表2 模型参数Tab.2 Important parameters

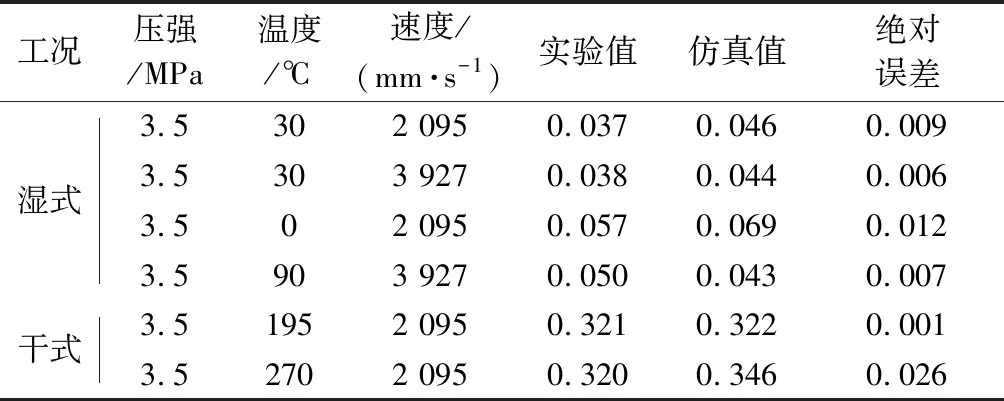
表3 摩擦因数对比分析Tab.3 Results ofexperiment and simulation

由表3可知，在湿式实验条件下，摩擦因数实验值与仿真值的绝对误差集中在千分位，而工程应用中摩擦因数的选取往往精确到百分位，表明该局部接触摩擦因数计算模型精度满足工程应用. 在干式高温实验条件下，仿真值与实验值相对误差小于9%. 两种润滑条件下摩擦因数仿真值与实验值吻合性较好，验证了模型的准确性.

3 模型分析及参数影响研究

为了得到摩滑过程中湿式铜基摩擦副局部接触状态下摩擦因数的变化规律，本文在实验验证的基础上进行了模型分析及参数影响研究.

应用表2所示模型参数及上文建立的局部接触摩擦因数计算模型对摩擦因数进行仿真计算，结果如图5～7所示.

在较高摩滑速度下，摩擦因数随温度变化趋势可分为4个阶段.

① 阶段A，摩擦因数随温度升高呈下降趋势，为混合润滑中的油膜主导阶段. 在该阶段，润滑油黏度随温升下降引起的摩擦因数减小程度大于相对油膜亏量α随温度增大引起摩擦因数的上升量；

② 阶段B，摩擦因数随温度升高而增大，为混合润滑中的微凸峰主导阶段. 为边界润滑与干摩擦的过渡阶段，在该阶段，相对油膜亏量α随温度增加引起摩擦因数增大程度大于润滑油粘度随温升下降引起摩擦因数的下降量；

③ 阶段C，摩擦因数随温度持续增加至最大值，为干摩擦中的摩擦因数升高阶段. 在该阶段润滑油膜由于高温发生分解失效，摩擦状态由混合润滑进入到干摩擦状态；

图5 温度对摩擦因数影响Fig.5 Influence of temperature on friction coefficient

④ 阶段D，摩擦因数随温度升高而下降，为干摩擦中的热衰退阶段. 该阶段摩擦层出现软化，摩擦表面出现黏着，磨损量陡增，摩擦因数下降.

在低摩滑速度下，由于油膜相对亏量α增大，摩擦因数升高，因此混合润滑中的油膜主导阶段A不再出现，直接进入到边界润滑中的微凸峰主导阶段B，如图5(b)所示.

局部接触区平均面压为2.1 MPa时，4种温度工况下，不同摩滑速度对应的摩擦因数如图6所示. 温度较高时，润滑油失效，摩擦系统处于干摩擦状态，摩滑速度对摩擦因数影响较小；温度较低时，油膜未发生分解失效，润滑状态仍为混合润滑，摩擦因数受相对油膜亏量α影响，摩擦因数随摩滑速度增加而下降，温度越低相对油膜亏量越小，摩擦因数随摩滑速度增大而衰减的特性越显著. 30 ℃工况下，摩滑速度由0升高到2 000 mm/s时，摩擦因数减小3倍.

图6 摩滑速度对摩擦因数影响Fig.6 Influence of sliding speed on friction coefficient

相对摩滑速度为3 927 mm/s时，4种温度工况下，不同压力对应的摩擦因数如图7所示. 局部接触区平均面压由1 MPa升高到10 MPa时，4种温度工况对应的摩擦因数几乎不变，如图7(a)所示. 当压力超过100 MPa时，接触面压力开始对混合润滑中的油膜主导阶段产生影响，此时摩擦因数随压力升高而增大，如图7(b)所示. 30 ℃工况下，压力由100 MPa升高到200 MPa时，摩擦因数增加1.4倍.