卸荷孔分布形式对液力变矩器轴向载荷影响规律分析

闫清东, 谭路, 魏巍, 宋泽民

(1.北京理工大学 车辆传动国家重点实验室，北京 100081；2.北京电动车辆协同创新中心，北京 100081；3.一汽-大众汽车有限公司成都分公司，四川,成都 610199)

高功率密度液力变矩器体积小且传递功率大，是重型车辆液力机械传动系统的核心部件[1]. 在液力变矩器结构的轴承、工作轮联接螺钉以及闭锁离合器设计和选型时，均需要考虑轴向力. 目前，减小液力变矩器轴向力的主要措施为在涡轮毂上均布开一组卸荷孔，使得高压泄漏区的工作液体流向低压泄漏区. 如图1所示虚段内的高压泄漏区液体流向涡轮与导轮之间的低压泄漏区，从而平衡这两个泄漏区中工作液体的压力，有效地减少高压泄漏区产生的轴向力.

图1 液力变矩器结构简图Fig.1 Structural diagram of hydrodynamic torque converter

此外，在泵轮和涡轮的结构设计上，若尽量使沿轴向左右两侧的圆盘结构对称，则左右两侧泄漏区中的工作液体作用在叶轮上的轴向力就可以相互抵消，同样达到减小轴向力的目的. 黄建勋等[2]通过研究开设卸荷孔前后的轴向力仿真结果的对比，得出在涡轮轮毂上开设卸荷孔能够有效降低变矩器外壳体与涡轮间传动油的压力，进而大幅减小作用在泵轮与涡轮上的轴向力.

文中采用 CFD 仿真技术分析不同参数的卸荷孔，即不同孔径、不同个数、不同分布圆半径的卸荷孔分别对变矩器轴向载荷及内部流场的影响，以期掌握卸荷孔参数对液力变矩器内外特性影响的规律，为变矩器实际使用过程中卸荷孔设计提供试验及理论指导依据，提升液力变矩器的可靠性.

1 计算模型

文中研究的液力变矩器循环圆直径为420 mm，泵轮、涡轮和导轮的叶片数分别为22、24、20. 如图2所示，液力变矩器的内流体主要分为三个部分：工作轮区、泄漏区、间隙区. 其中虚线圆所在区域为变矩器循环圆，工作轮区为循环圆通过的泵轮、涡轮和导轮的工作腔区. 图中ai、fj、ch所示区段为外泄漏区，dg所示区段为内泄漏区；ab、ef、cd所示区段为循环圆中叶轮之间的间隙区，卸荷孔位于涡轮毂上，使ch段内的高压流体能流向fj段. 同时规定轴向力方向向左为正，向右为负.

图2 液力变矩器计算简图Fig.2 Calculation diagram of hydrodynamic torque converter

建立了液力变矩器全流道几何模型，对于卸荷孔处流体，均采用一组圆孔. 为分析卸荷孔的三个参数对于轴向力大小的影响规律，文中对其进行了正交试验与单因素试验,见表1～表3.

表1 因素水平表

卸荷孔布置形式由卸荷孔分布圆半径rf，卸荷孔数n以及卸荷孔径rh确定. 考虑到液力变矩器的尺寸大小以及结构布置，卸荷孔分布圆半径的范围为65～85 mm，卸荷孔数为4～12个，卸荷孔径的范围为8～12 mm. 将卸荷孔分布圆半径、卸荷孔数、卸荷孔径分别记为因素A、B、C.

考查指标为各个工作轮所受的轴向力. 确定因素水平表，如表1所示.

选择合适的正交表头设计. 从因素水平表看，为3因素3水平，可选用L933正交表，3个因素按顺序占1、2、3列，见表2.

表2 正交试验表

确定的单因素参数范围如表3所示.

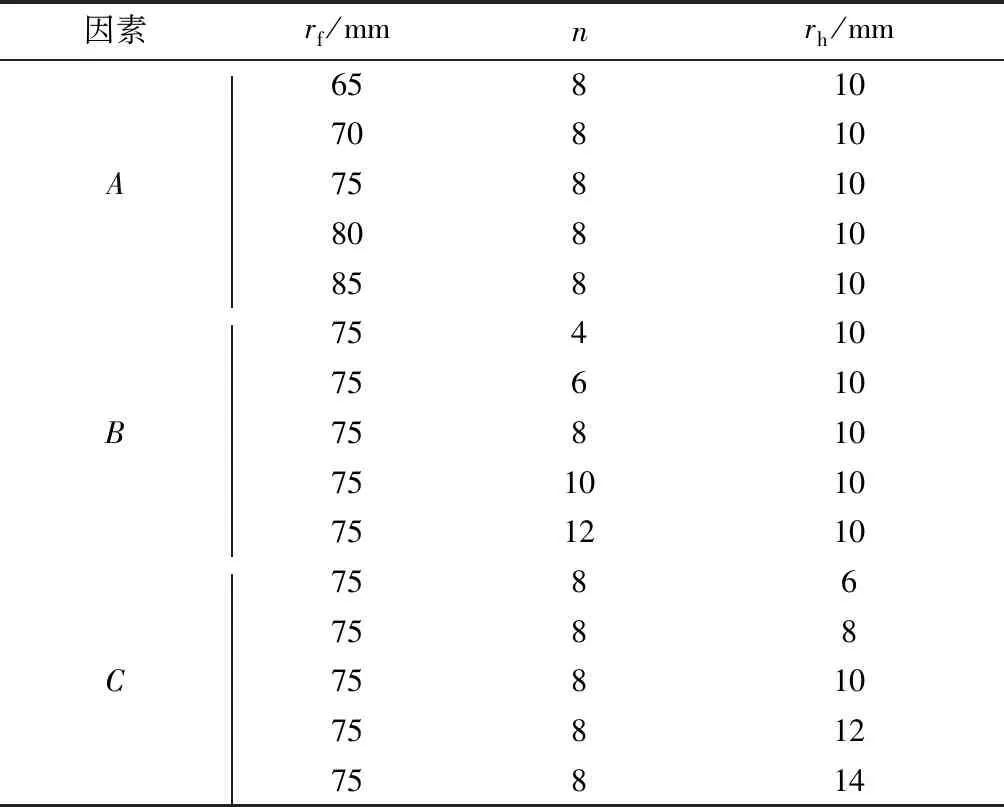
表3 单因素试验参数范围表

根据试验设计建立不同的液力变矩器内流体模型，为了保证其可比性，在这些模型中，只有卸荷孔处的流体模型不同，泄漏区、泵轮、涡轮以及导轮处的流体模型都是相同的，如图3所示.

图3 内流体模型Fig.3 Model of the fluid

2 CFD仿真

仿真实验假设[3-5]：

① 液力变矩器所有元件均视为绝对刚体，忽略流固耦合引起的流道网格变形；

② 工作介质为不可压缩黏性流体，在工作过程中其密度、黏度等保持不变；

③ 流场温度恒定，不考虑液力变矩器内工作介质与工作轮叶片的热交换；

④ 循环流道流场完全封闭，不考虑液力变矩器内流道的冷却循环及容积损失，流道中任意横断面的流体总量相等，满足连续性方程；

⑤ 忽略作用于流体上的质量力.

由上述假设条件可得其应满足质量守恒方程和动量守恒方程[6].

将建立的液力变矩器内流体模型导入ICEM中进行四面体网格划分. 其中泵轮与涡轮流体的结构是确定的，导轮与外泄漏区流体的结构是变化的. 划分出的泵轮与涡轮网格如图4所示，泵轮共1 941 228个网格，涡轮2 033 700个网格.

图4 各部分流体网格Fig.4 Mesh of the domains

对于导轮与外泄漏区流体，使用前文正交试验建立的模型划分出的网格非常接近，导轮约2 000 000个网格，外泄漏区约810 000个网格，划分出的网格与图4(c)和4(d)相似.

文中CFD仿真采用的湍流模型为剪应力输运(SST)模型. 设置流场数值模拟初始条件：将四部分流体分别设置成单相流域，设置参考压力为0.3 MPa，将ah区段外泄漏区流体的转速设为泵轮与涡轮的平均转速. 泵轮转速设为2 000 r/min，导轮固定. 文中正交试验模拟了涡轮转速按传动比i=0、0.8取值时的两种工况，单因素试验研究了涡轮转速按传动比i=0、0.2、0.4、0.6、0.8取值时的5种工况. 设定工作温度75 ℃，液力传动油密度为860 kg/m3，动力黏度为19.6×10-3Pa·s. 流场求解采用迎风模式(Upwind)，计算精度为动量、质量的均方根值小于10-5，初始迭代次数为300次，在不满足均方根植小于10-5时可以增加迭代次数.

3 结果分析

将CFD计算结果的原始特性曲线与试验值进行了对比，两者吻合度较高，CFD计算结果较为准确. 如图5所示，通过对比不同卸荷孔计算模型的特性曲线，发现卸荷孔的改变不会对液力变矩器外特性产生明显影响，变矩器性能主要受工作轮的叶栅结构影响.

图5 原始特性曲线对比图Fig.5 Comparison diagram of the original characteristic curve

在CFD计算模型中，泵轮受到三部分的轴向力：油液对泵轮内外环和叶片的力、ch区段中油液对泵轮外壳的力、ai区段中油液泵轮轴承座的力；涡轮受到自三部分的轴向力：油液对涡轮内外环和叶片的力、ch区段中油液对涡轮外壳的力、fj区段中油液对涡轮毂的力；导轮受到三部分的轴向力：油液对导轮内外环和叶片的力、ai区段中油液对单向离合器外环的力、fj区段中油液对单向离合器外环的力.

基于以上分析，提取各部分轴向力后，发现ch区段中油液产生的轴向力使泵轮和涡轮有互相靠近的趋势，而油液冲击叶轮流道产生的力使泵轮和涡轮有互相分开的趋势.

在建立CFD计算模型时，简化了图2中dg段的内环内空腔中的泄漏区流体，此部分油液的流动将对工作轮的产生轴向力，因此，将这部分轴向力采用如下的束流理论公式进行计算，修正CFD仿真结果. 根据如下的伯努利公式计算dg段内半径R处的压力P为

(1)

式中：Pd为d点的压力，vd为d点的绝对速度.

假定dg段中无能量损失，此点的轴面速度与d点处相等、环量相等，则可得

式中：i为速比;ωB为泵轮的角速度. 根据如下公式计算出dg段的轴向力Fshaft为

式中：Fshaft为轴向力；Rd为d点的半径；Rg为g点的半径.

计算出修正后的无卸荷孔的各工作轮轴向力如图6所示，涡轮和导轮受力方向一致，与泵轮相反，泵轮与涡轮有互相吸引的趋势，在下文中三个叶轮受载方向不变，只研究受载大小，故用绝对值表示轴向力大小.

图6 无卸荷孔时轴向力分布图Fig.6 Thrust forces in the absence of balance hole

将表2中的9组正交试验的模型进行仿真计算，得到起动工况下得轴向力如图7所示.

图7 起动工况轴向力对比图Fig.7 Thrust forces at starting operation

表值表

表5 R值表

极差R越大，表明此因素对于指标的影响越大. 由表5可以看出，在试验所选取的因素变化范围内，在两种速比下，卸荷孔分布圆半径对泵轮和涡轮所受轴向力的影响最大，其次为卸荷孔数，卸荷孔径的影响最小.

由图6可以看到，液力变矩器在低速比时受到的轴向力要大于高速比时工作轮所受的轴向力. 减少在低速比时叶轮所受的轴向力能更好地保护液力变矩器及轴承. 根据表4可以得出的轴向力最小得方案为A3B3C3，但理论最优方案并没有出现在正交试验中，为了验证其是否为最佳方案，对A3B3C3进行计算.

建立卸荷孔分布圆半径85 mm，卸荷孔数为12个，卸荷孔径为12 mm的内流体模型，导入CFX中进行仿真计算，参数设置与前文相同，得到其轴向力分布如表6所示.

表6 A3B3C3最佳方案轴向力

A3B3C3方案中，在起动工况时，泵轮和涡轮的轴向力分别为24.1、17.0 kN，其余方案中泵轮轴向力为24.2～26.8 kN，涡轮轴向力为17.1～20.0 kN，说明此方案确实为最佳方案.

对三个参数分别使用单因素试验研究各自对轴向力的影响，研究结果如下.

3.1 卸荷孔分布圆半径对轴向力的影响

由图8可以看出，在各个速比中，卸荷孔分布圆半径对于泵轮与涡轮轴向力影响较大. 卸荷孔分布圆半径越大，泵轮与涡轮所受轴向力越小，即减荷效果越好. 分布圆半径65 mm的卸荷孔方案可以将泵轮所受的轴向力减小至57.7%～72.8%，而分布圆半径85 mm时可以减少至53.3%～66.7%，减荷效果增加约5%，即轴向力再减小2 kN左右；对于涡轮，后者比前者减荷效果增加5%～8%，约1.2～3.2 kN，优化减荷效果明显.

图8 分布圆半径对轴向力的影响Fig.8 Influence of distribution circle radius for thrust forces

分析其原因是因为在液力变矩器中，泵轮与涡轮所受的轴向力很大一部分是来自外泄漏区. 在泄漏区中，流体受到的是离心力，且距离旋转中心越远，受到的离心力越大，所以在距离旋转中心较远处开卸荷孔可以更多地减少流体受到的压力，从而有效减少泵轮与涡轮的轴向力. 导轮所受的轴向力有略微的上升，这是由于图1中的ch段高压流体通过卸荷孔通到了fj段中，从而增大了fj段中的流体压力，使导轮增大了受力.

由表5中可以看出卸荷孔分布圆半径的影响在低速比时要大于高速比时. 在低速比时，卸荷孔分布圆半径对变矩器轴向力的影响在这三个因素中是占有决定性的,在高速比时，其影响有所削弱.

3.2 卸荷孔数对轴向力的影响

由图9可以看出，在低速比时，泵轮与涡轮的轴向力随着卸荷孔数的增加而减小，但是卸荷孔数的从4个增加到12个，对泵轮和涡轮提升的减荷效果不显著，12个卸荷孔的减荷效果仅比4个卸荷孔增加了1%左右，减少约0.5 kN，故卸荷孔数对于轴向力的影响不显著.

图9 卸荷孔数对轴向力的影响对比图Fig.9 Influence of hole number for thrust forces

在中高速比时，轴向力随着卸荷孔数的增加先增大后减小，存在一个临界卸荷孔个数使得轴向力最大.

3.3 卸荷孔径对轴向力的影响

由表5可以得出，卸荷孔径在高速比工况对轴向力的影响大于在低速比工况的影响.

由图10得出在低速比工况时，轴向力随着卸荷孔径的增大而减小，孔径14 mm比孔径6 mm的减荷效果更好，轴向力减小1.7%，约0.6 kN. 在高速比工况，轴向力反而会随着卸荷孔径的增大而增大，轴向力增加2.0%，约0.5 kN.

图10 卸荷孔径对轴向力的影响对比图Fig.10 Influence of hole diameter for thrust forces

虽然卸荷孔径对轴向力的影响不明显，但是设计卸荷孔时可根据具体应用场景选择卸荷孔径的尺寸，如在工程机械中的液力变矩器长时间工作于中低速比工况，可选择大孔径卸荷孔，对于道路车辆长时间工作于中高速比工况，则可选择小孔径卸荷孔，有利于保护液力变矩器与轴承.

4 结 论

卸荷孔对泵轮与涡轮受到的轴向力减荷效果明显，对变矩器外特性的影响可以忽略. 卸荷孔的变化对导轮受到的轴向力影响不明显.

卸荷孔分布圆半径对轴向力的影响最大，其次为卸荷孔数，卸荷孔径影响最小. 泵轮和涡轮所受轴向力的大小随着卸荷孔分布圆半径的增加而显著减小；低速比时，泵轮和涡轮所受轴向力的大小随着卸荷孔径的增大而减小，随着卸荷孔数的增加而增加；高速比时，泵轮和涡轮所受轴向力的大小随着卸荷孔径的增大而增大，存在一个临界卸荷孔数使得轴向力最大.

文中设计的最优卸荷孔布置方案使得泵轮所受轴向力能减小约47%，涡轮所受轴向力能减小大约57%，同时导轮所受轴向力会增加约5%，由于导轮轴向力较小，以略微增加其轴向力来大幅度减小其他两轮所受轴向力是可取的.

设计卸荷孔时可考虑具体应用场景，对于长时间工作于低速比工况的工程机械用变矩器，应选择较大卸荷孔分布圆半径、较大孔径和较多卸荷孔数，而安装于道路车辆中的变矩器以中高速比工况比为主，选择较小孔径卸荷孔，数量设置为8～10个，减荷效果最佳. 由于孔径和孔数对轴向载荷的影响较小，综合考虑变矩器结构强度后合理设置分布圆半径即可显著减小轴向力.