基于协整理论的高等教育与区域经济长短期关系实证分析——以山西省为例

赵 静

(山西大学商务学院,山西 太原 030031)

亚当·斯密早在《国富论》中就提出教育的发展能够促进经济的增长这个理念,而后舒尔茨、埃茨科瓦茨、雷德斯道夫等学者对高等教育与经济发展互动关系做了大量的理论研究,丰富了教育对经济增长贡献的理念。邓小平在1977年指出:“我们要实现现代化,关键是科学技术要能上去。发展科学技术,不抓教育不行”,之后在1987年党的十三大会议上提出“百年大计,教育为本”。习近平主席在2014年11月的亚太经合组织(APEC)工商领导人峰会上指出，中国经济呈现出新常态,要从要素驱动、投资驱动转向创新驱动推动我国经济的增长,创新驱动成为持续内在增长驱动力,而创新驱动的原生动力在于高质量的教育。可见,教育是经济发展的持续动力,二者互动发展是我们关注的一个持久性话题。

从2013年开始，山西省经济呈现下行态势,GDP总量由原来全国排名居中下滑到全国末尾。2015年人均GDP排名列全国第27位,2016年人均GDP进一步下滑到第28位,且2016年GDP增速排名全国倒数第二。对于山西这个以能源煤炭为经济增长主动力的省份来说，进行产业结构调整、寻找经济增长的新突破口迫在眉睫,因此需要各方面各层次加强创新,而高等教育可以为我省全面深化改革提供强有力的技术型人才、管理型人才等层面的支持,人力资本是进行创新的主体。

我国高校自1999年开始扩大招生,从此全国进入大众化教育阶段,目前理论和实践都证明我国高等教育进入了后大众化阶段。2016年山西省高等教育毛入学率达到43.1%,正在跨入毛入学率为50%的普及化阶段。然而在经济发展增速放慢的新常态下,在高等教育发展多元化的今天,经济发展与高等教育之间的关系又如何呢?因此研究高等教育与区域经济的长短期关系对把握高等教育的发展方向、提高高等教育的发展水平、促进经济的持续发展具有重要的现实意义,同时对丰富该领域的研究具有重要的理论意义。

一、研究现状

高等教育与经济协调发展的实证研究主要从以下两种实证研究方法展开:一是统计分析法，二是应用计量分析法。

统计分析法重在对代表教育发展水平与经济发展水平的指标的选取,然后利用主成分因子分析、主成分分析、灰色关联模型等统计分析法来研究二者的协调性。选取代表教育发展水平与经济发展水平的单项指标在全国的排位比较来分析二者的协调程度,该方法操作简便易行,直观明了。赵静(2017)将全国31个省、市、自治区的高等教育水平与经济发展水平分别进行划分,分为发达地区、中等发达地区、欠发达地区,指出二者的排名不论高低，只要在同一个区域范围就可视为高等教育与经济协调发展类型,反之就为高等教育与经济失调发展类型。通过分析发现，2008—2012年,山西省高等教育发展水平和经济发展水平都处于中等水平,二者属于协调发展类型，从2013年开始,山西省高等教育与经济发展水平处于失调状态。另外一种统计分析法较为复杂,主要是通过建立指标体系使用因子分析、主成分分析、灰色关联模型等来鉴定高等教育发展水平和经济发展水平,不再是单个指标的排位比较,而是综合比较。毛盛勇(2009)选取2006年我国31个省区市的经济和高等教育的截面数据，采用因子分析法计算了31个省区市的高等教育水平和经济发展水平的因子得分,然后利用因子得分排序进一步计算等级差和相关系数。研究表明:31个省区市中,高等教育与经济发展协调程度为好和较好的有12个,差和较差的有13个,协调程度一般的有6个,总体协调程度较差。张耀文(2013)通过构建指标体系，利用因子分析、主成分分析法测算了各个省份的高等教育水平指数,再采用泰尔指数测度了经济发展水平,而后使用VAR计量分析了二者的协调关系。王永杰等(2016)通过2000—2009年我国高等教育与经济发展的相关数据构造了指标体系,利用灰色关联分析法分析了二者的协调程度。研究发现:西部协调值最高,东部次之,中部最低;但西部地区的协调质量低,东部地区的协调质量较高,中部地区的协调质量居中。

应用计量分析法主要通过协整理论、VAR模型、ECM模型、VEC模型、格兰杰因果检验等方法来分析高等教育与经济发展的关系。毛建青(2010)选取浙江省1981—2006年的数据分析发现，二者之间存在长期稳定的协整关系,高等教育规模是经济发展的原因,反之则不成立,二者只存在单向的互动关系。王旭辉(2014)采用福建省 1978—2012 年统计数据分析发现，高等教育规模与经济增长之间存在长期稳定的协整关系,福建省高等教育规模与经济增长互为格兰杰因果关系。陶韶菁、白争辉(2016)选取广东省1978—2014年的数据分析发现，高等教育与区域经济之间存在长期稳定的协整关系,高等学校在校生人数是经济发展的格兰杰原因,但经济增长并不必然导致高等学校在校生人数的增长。

本文在学习总结该研究领域优秀研究成果的同时,也发现了研究中存在的不足,由于每个研究者采用的样本不同，因此结果不尽相同,另外同样的研究方法采用不同的样本也会得出不同的结论。因此本文在研究方法上,继承了协整理论研究方法的优势,引入邹氏稳定性检验法,对比分析在不同时间段高等教育与区域发展水平的长短期关系的差异。

二、数据处理与说明

(一)指标选取说明

代表经济发展水平的指标很多,人均地区生产总值最能体现经济发展的内涵,同时本文对人均地区生产总值进行了价格调整,以1980年为基期水平,用居民消费价格指数进行调整。调整后的人均地区生产总值用GDP表示,未调整的人均地区生产总值用NGDP表示,单位是元/人,1980—2016年调整前后二者的线性比较图如图1所示。通过图1可以看出,未调整的人均GDP增长速度要明显快于调整后的人均GDP,其中很大一部分原因是价格上涨带来的数值增长,因此可比价格的人均GDP才能真正反映经济的实际增长情况。

本文选用在校学生人数代表高等教育的发展程度,用STU表示,单位是万人,图2显示了1980—2016年山西省普通高校在校学生人数的发展情况,1999年之前普通高校在校生人数平稳发展, 1999年以来高校学生规模迅速扩张,开启了我省高等教育发展的热潮。

人均GDP的数据、高校在校学生人数均来源于国家统计局网站,调整后的人均GDP由笔者整理计算得出,其中2016年在校学生人数的数据由《山西省2016年教育事业发展统计公报》推算得出。

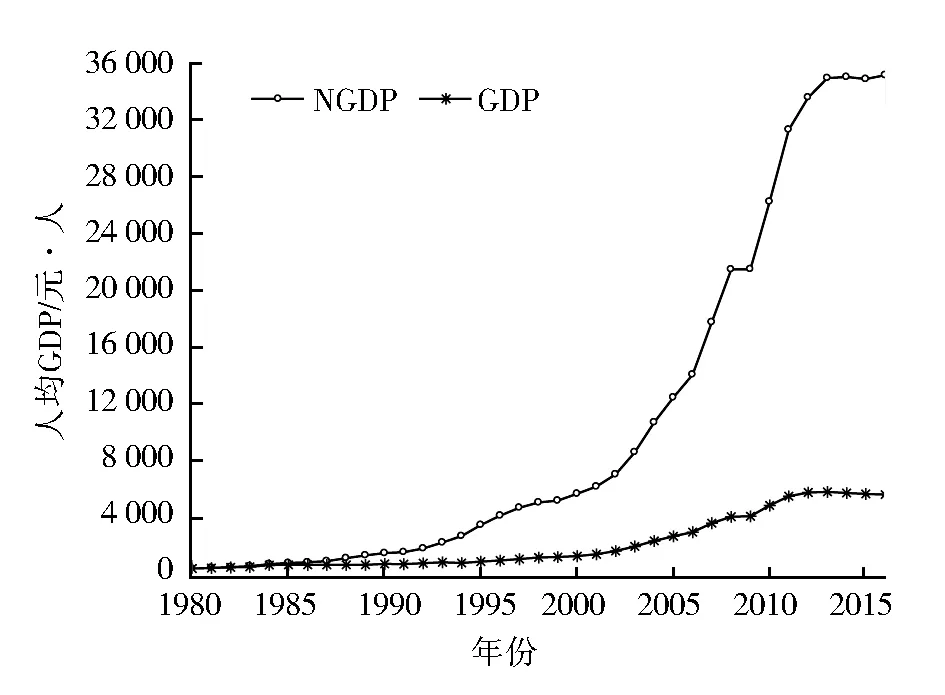
图1 调整前后的人均GDP

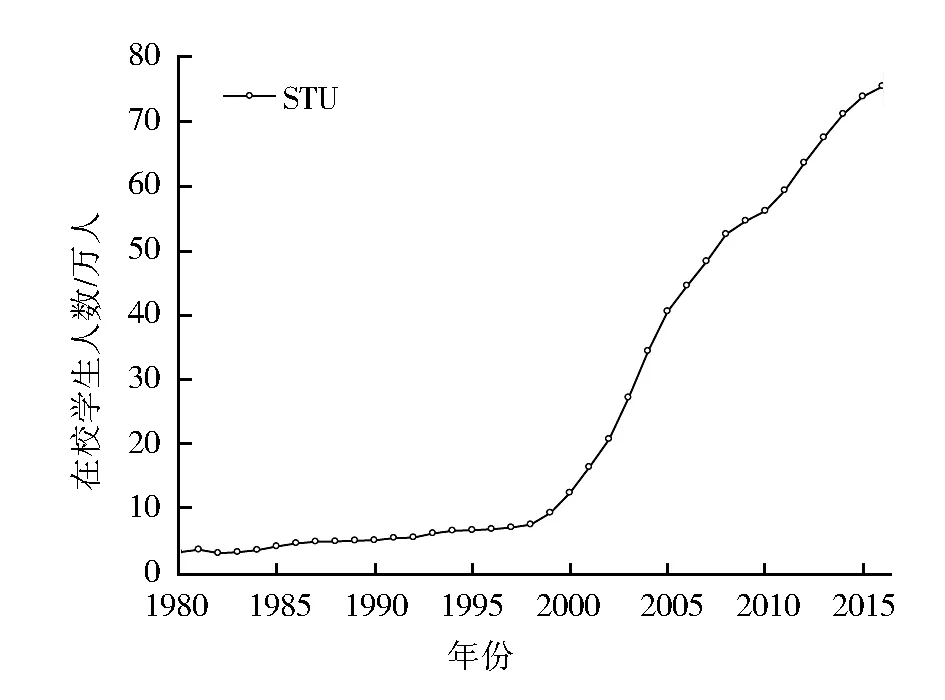
图2 在校学生人数线性图

(二)数据平稳性检验

通过观察图1和图2,可以看到价格调整后的人均GDP和在校学生人数STU都存在明显的上升趋势,初步判断数据并不平稳,对原始数据取自然对数,再对新变量采用ADF法进行平稳性检验,检验结果如表1所示。本文计量分析采用Eviews5软件包进行操作。

从表1可以看出,原始数据人均GDP和在校学生人数STU都是非平稳时间序列,同时取自然对数后的lnGDP和lnSTU也是非平稳的,但是lnGDP和lnSTU的一阶差分dlnGDP和dlnSTU均是平稳时间序列,因此lnGDP和lnSTU是一阶单整序列。

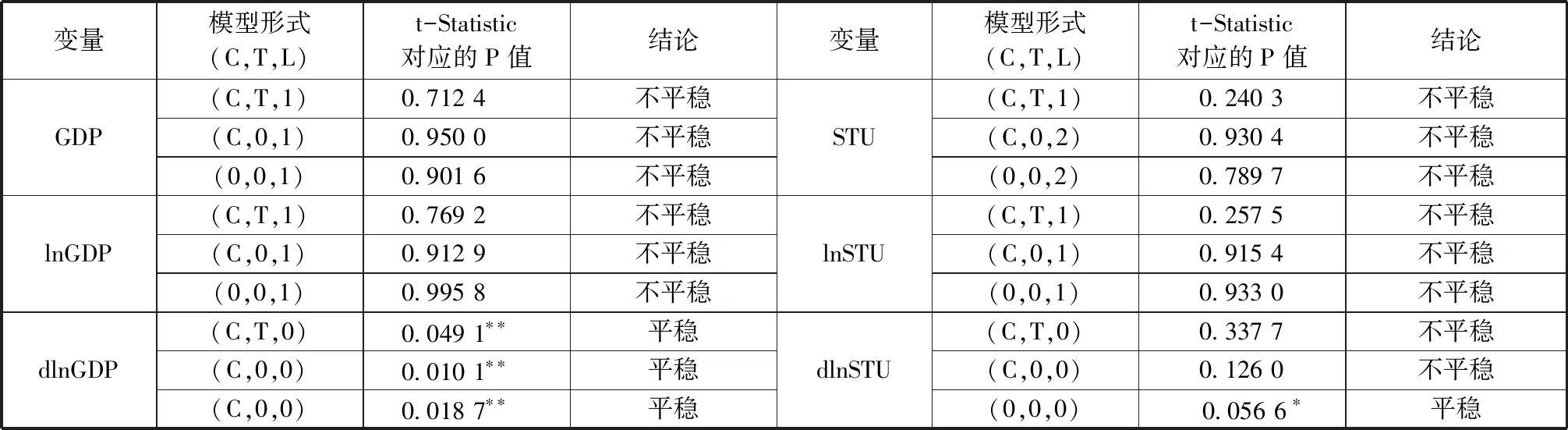
表1 ADF检验结果

注:模型形式(C,T,L)中,C表示截距项,T表示时间趋势项,L表示滞后阶数,滞后阶数根据SIC准则进行确定。*、**、***分别表示10%、5%、1%的显著性水平上拒绝存在单位根的原假设。dlnGDP和dlnSTU代表lnGDP和lnSTU的一阶差分。

三、高等教育与区域经济协调发展实证研究

(一)高等教育与区域经济长期关系研究

协整指因变量和自变量之间存在一个长期的均衡关系,即变量之间存在一种稳定的长期关系。通过协整检验可以避免变量之间的伪回归现象。本文通过协整理论验证高等教育和区域经济之间的长期关系,同时采用邹氏检验来分析模型的结构稳定性,以保证不同时间段内高等教育和区域经济之间长期关系的稳定性。

1.长期协整检验。协整检验的方法主要有Johansen协整检验和EG两步法,两种方法各有优劣。本文首先采用Johansen协整检验法说明山西省高等教育和区域经济之间是否存在协整关系,然后进一步采用EG两步法证明协整关系以及具体结构参数。

表2基于迹检验统计量的Johansen协整检验的结果显示,针对第一个模型协整方程个数为零的原假设,在5%的显著性水平下,由于迹检验统计量对应的P=0.000 7小于5%,因此拒绝模型协整方程数为零的原假设;针对第二个模型协整方程数至多为一个的原假设,由于迹检验统计量对应的P=0.132 6大于5%,因此不拒绝至多一个协整方程的原假设,说明高等教育和区域经济之间存在一个协整关系。

表3基于最大特征值统计量的Johansen协整检验的结果显示,针对第一个模型协整方程个数为零的原假设,在5%的显著性水平下,由于最大特征值统计量对应的P=0.000 9小于5%,因此拒绝模型协整方程数为零的原假设;针对第二个模型协整方程数至多为一个的原假设,由于最大特征值统计量对应的P=0.132 6大于5%,因此不拒绝至多一个协整方程的原假设,说明高等教育和区域经济之间存在一个协整关系。

表2 基于迹检验统计量的Johansen 协整检验(全部数据)

注:检验模型滞后阶数为2。

表3 基于最大特征值检验统计量的Johansen 协整检验(全部数据)

注:检验模型滞后阶数为2。

从表2和表3的检验结果可以看出,不管是基于迹检验统计量还是基于最大特征值检验统计量的Johansen检验,都表明在5%的显著水平下,lnGDP和lnSTU都存在一个协整方程,即二者之间是(1,1)阶协整的。

基于全部数据估计的长期协整模型如下:

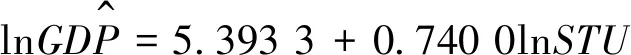
(模型1)

T-stats=(95.09) (37.20)

Prob.=(0.000 0) (0.000 0)

R2=0.975F-stats=1 384.048n=37

模型结果显示lnSTU对应的T统计量的P值等于0,小于5%,因此对lnGDP的影响显著。采用EG两步法进一步证明模型的协整关系,提取上述模型1估计的残差,利用ADF检验法,采用(0,0,1)形式的模型检验得到T-statistic=-3.069 6(P=0.003 1),P值小于5%的显著性水平,表明残差是平稳的,同时也证明了经济发展dlnGDP 和高校发展dlnSTU之间存在长期的协整关系。

2.结构稳定性检验。在经济模型里,各变量相互之间的关系有时会因某些外部冲击或自身性质的改变而发生结构性的变化。如果我们忽视这一变化,仍然同时利用变化前后的数据进行回归分析,则模型的精确度就会大大降低,利用模型所做的估计、推断与预测就可能得出错误的结论。因此,对模型进行结构稳定性检验是必要的,而邹氏检验(Chow’s test)即为检验模型结构稳定性的一种较为简单的方法。

1999年，我国政府基于解决经济和就业问题而施行了扩大普通高校本专科院校招生人数的教育改革政策。自高校扩招政策实施以来,我国高等教育发展迈上了新台阶,这一政策的实施导致高校发展规模在1999年可能会发生结构性的变化。为了验证上述猜想,我们在模型1的基础上选定1999年为可能发生结构变化的转折点进行邹氏检验,结果如表4所示。

表4 Chow Breakpoint Test:1999

检验结果显示,F统计量对应的P值为0.018,在5%的显著性水平下,拒绝模型结构稳定的原假设,说明1999年高等教育规模增长的确发生了结构性变化。基于此,我们将分时段进行回归分析。

3.分时段回归分析。为了提高模型的估计精度,验证不同时间段高等教育和区域经济之间协整关系的稳定性,本文将1980—1998年划分为样本1,包括19个样本数据,1999—2016年划分为样本2,包括18个样本数据,协整回归结果如表5整理所得。采用EG两步法检验二者的协整关系,结果显示,分时段样本和采用全部样本一样,高等教育和区域经济之间存在长期稳定的协整关系,在5%的显著性水平下,lnSTU对lnGDP的影响显著。不同的是分时段回归长期弹性系数和使用全部数据有区别,具体如表6所示。

采用1980—2016年的全部样本数据显示,高校在校人数每增加1%,平均来说人均GDP增长0.74%;1980—1998年的样本数据显示,高校在校人数每增加1%,平均来说人均GDP增长0.892 8%;1999—2016年的样本数据显示,高校在校人数每增加1%,平均来说人均GDP增长0.850 7%。分时段回归提高了估计的精度,长期弹性系数均比全部样本的要高,这为决策提供了更可靠的数值论据。

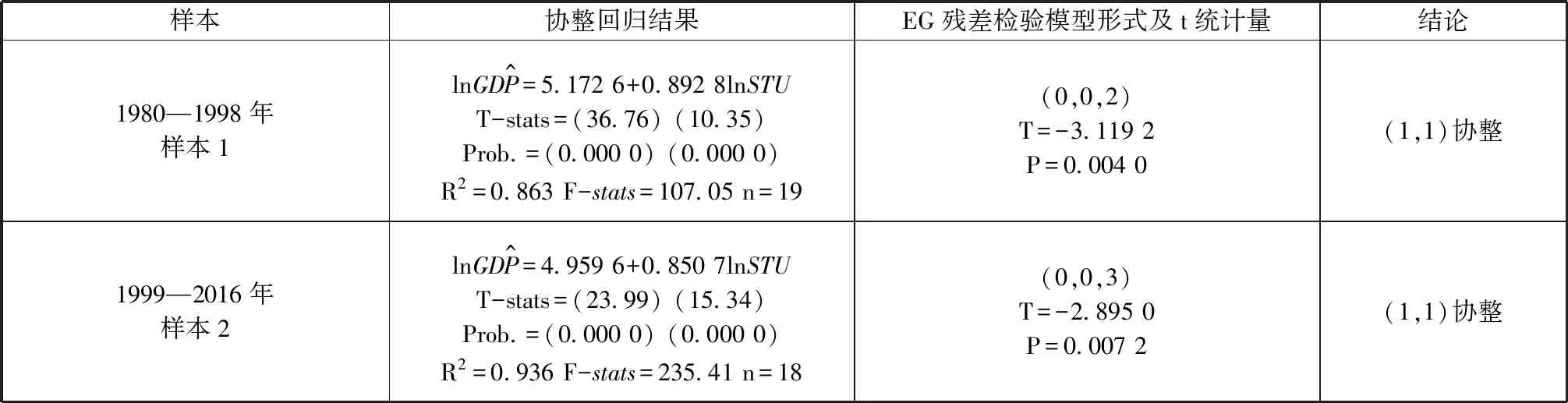
表5 分时段协整回归

表6 分时段协整回归长期弹性系数

(二)高等教育与区域经济短期关系研究

两个变量之间即使有长期均衡关系,但在短期内也会出现失衡。误差修正模型(ECM)的优点在于提供了解释长期关系和短期调节的途径,我们可以用ECM对这种短期失衡加以修正。那么变量之间的关系是否都可以通过误差修正模型来表述呢？1987年恩格尔和格兰杰提出了著名的格兰杰表述定理:如果变量X与Y是协整的,则它们间的短期非均衡关系总能由一个误差修正模型表述。即：

ΔYt=lagged(ΔY,ΔX)-λ·ecmt-1+μt

其中,λ是短期调整参数,0<λ<1,ecmt-1是非均衡误差项。

分时段误差修正模型的回归结果如表7所示。通过表7可以看到，全样本和样本2回归ecmt-1项对样的T统计量在5%的显著性水平下都是显著的解释变量,并且符号均为负号,符合误差修正机制的原理。对于样本1的误差修正回归结果,ecmt-1项对样的T统计量在5%的显著性水平下不显著,通过尝试在模型中增加dlnGDP和dlnSTU的滞后期也没有得到比较理想的结果。对比全样本和样本2的回归,笔者认为尽管ecmt-1在5%的水平下不显著,但是符号为负符合误差修正机制的原理,并且其估计的数值结果和使用全样本和样本2形式上相似,因此如果放宽显著性水平到20%,这也不是一个很大的概率,因此表7中利用样本1做出的ECM也是合理的。

总之,采用1980—2016年的全部样本数据显示,dlnGDP关于dlnSTU的短期弹性系数为0.459 8,上一期lnGDP的实际值与长期均衡值之间的偏离在本期约23.21%得以修正;1980—1998年的样本1数据显示,dlnGDP关于dlnSTU的短期弹性系数为0.483 9,上一期lnGDP的实际值与长期均衡值之间的偏离在本期约28.68%得以修正;1999—2016年的样本2数据显示,dlnGDP关于dlnSTU的短期弹性系数为0.557 1,上一期lnGDP的实际值与长期均衡值之间的偏离在本期约29.91%得以修正。分时段回归提高了估计的精度,短期弹性系数均比全部样本的要高。

表7 分时段误差修正模型

注:e、e1、e2分别是由全部样本、样本1和样本2的长期均衡模型提取得到。

(三)高等教育与区域经济因果关系研究

高等教育与区域经济协调、良性循环互动发展是各地方政府努力的方向。然而,究竟是高等教育的发展拉动了区域经济的发展,还是区域经济的发展促进了高等教育的发展,研究二者的因果关系对政府部门做出行政决策具有重要意义。格兰杰因果检验就是确定一个变量的变化是否是另一个变量变化的原因的一种有效的方法。

虽然回归分析考虑了一个变量对另一个变量的依赖关系,但这并不意味着因果关系,换言之,变量间某种关系的存在不能证明是因果关系或者影响力的方向。若两个变量X和Y是协整的,而且每个变量都是一阶单整I(1)，即都是不平稳的,那么,要么X一定是Y的格兰杰原因,要么Y一定是X的格兰杰原因。由于高等教育与区域经济之间存在协整关系,因此二者之间一定存在一个方向的格兰杰原因。

格兰杰因果关系检验结果如表8、表9、表10所示。采用1980—2016年的全部样本数据显示,在10%的显著性水平下,原假设下F统计量对应的P值均小于10%,因此高等教育和区域经济间存在双向的格兰杰因果关系;1980—1998年的样本1数据显示,在10%的显著性水平下,原假设下F统计量对应的P值均小于10%,同样表明高等教育和区域经济之间存在双向的格兰杰因果关系;1999—2016年的样本2数据显示,在10%的显著性水平下,dlnSTU不是dlnGDP的原假设下F统计量对应的P值=0.079 88小于10%,说明高等教育是经济发展的格兰杰原因,而dlnGDP不是dlnSTU的原假设下F统计量对应的P值=0.203 94大于10%,说明经济发展不是高等教育发展的格兰杰原因。

综上可知,利用全样本与样本1分析时，高等教育和区域经济间存在双向的格兰杰因果关系；利用样本2分析时，存在单向的格兰杰原因,高等教育是经济发展的格兰杰原因,经济发展不是高等教育发展的格兰杰原因,可见现阶段高等教育和经济发展不能良性互动发展,高等教育依然能够在一定程度上促进经济发展,高等教育的消费依然是经济增长的一个驱动力,但是经济发展没有能够反过来作用于高等教育。

表8 全样本格兰杰原因结果

注:Lags4

表9 样本1格兰杰原因结果

注:Lags2

表10 样本2格兰杰原因结果

注:Lags2

四、结论及政策建议

(一)结论

通过对山西省高等教育与区域经济的长短期关系实证研究,主要得到以下结论:

1.邹氏检验表明，1999年高等教育规模增长确实发生了结构性变化,不再适合用全部样本进行分析,为了提高模型的估计精度,据此将样本分为全部样本(1980—2016年)、样本1(1980—1998年)和样本2(1999—2016年)三个时段比较分析二者之间的长短期关系。

2.协整模型估计结果表明，不同时段二者之间均存在长期协整关系,且长期弹性系数不同,全部样本、样本1和样本2对应的长期弹性系数分别为0.740 0、0.892 8和0.850 7,因此高等教育发展水平的提高依然是经济发展的动力。从数值上看,通过采用样本1和样本2的数据分别进行估计，结果显示高校扩招后高等教育对区域经济的贡献没有太大区别,分时段估计值较全部样本增长率要高,模型精度更高。

3.误差修正模型估计结果显示，不同时段二者之间均存在误差修正机制,且短期弹性系数不同,全部样本、样本1和样本2对应的短期弹性分别为0.459 8、0.483 9和0.557 1,分别对应的误差修正量为23.21%、28.68%和29.91%。从误差修正机制数值的大小来看,样本2短期偏离较大,修正的更多；并且样本2对应的短期弹性系数明显较大,说明现阶段高等教育的发展对经济发展水平的提高具有明显的作用。

4.格兰杰因果检验结果表明，利用全样本与样本1分析时，高等教育和区域经济

间存在双向的格兰杰因果关系,利用样本2分析时存在单向的格兰杰原因。高等教育是经济发展的格兰杰原因,经济发展不是高等教育发展的格兰杰原因,可见现阶段山西省高等教育和经济发展不能良性互动发展。

(二)政策建议

1.顺应时代要求，把握高等教育发展方向，提高高等教育质量。研究结果表明，山西省高等教育对经济发展具有明显的促进作用,高等教育仍然是经济持续发展的推动力。在山西省经济结构转型的今天,山西省高等教育发展一定要积极转变方向,培养顺应时代要求的人才;不断提高教育质量,培养创新能力强的人才,为山西省的经济发展添砖加瓦。

2.进一步加大经济发展对高等教育的反哺。格兰杰因果检验结果表明，高等教育是经济发展的格兰杰原因,经济发展不是高等教育发展的格兰杰原因。为了促进二者良性互动发展,加大政府对高等教育的投入力度,同时鼓励提倡企业对教育的投入,支持学术研究,产学研相结合实现“双赢”;支持大学生就业,而非利用经济不景气和就业压力发“国难财”,造成人才流失,知识外溢,而这一方面我省在相关政策和经验方面做得还不够。