N掺杂LaAlO3电子结构的第一性原理研究

李 强，谭兴毅

(1.湖北民族大学新材料与机电工程学院，恩施 445000;2.湖北民族大学新材料成型及装备技术产学研中心，恩施 445000)

1 引 言

钙钛矿结构氧化物(ABO3)具有丰富的物理和化学性质，广泛应用于人类的生产、生活中，其命名源于矿物质钙钛矿(CaTiO3)[1]。理想的ABO3属于立方晶系，空间群为Pm3m(No.221)，单胞中原子的分数坐标为：A (0,0,0)，B (1/2,1/2,1/2)，O (1/2,1/2,0)。一般而言，A位是半径较大的稀土或碱土元素离子，其化学价可以是+1，+2，+3价；相应的B位为半径较小的过渡元素离子，其化学价为+5，+4，+3价；而O离子价态固定为-2价；并且要组成ABO3型钙钛矿结构，离子A，B，O的半径应满足紧密堆积原则，即[1]:

式中RA,RB和RO分别为A, B和O离子的半径，t为容忍因子。一般情况下，t介于0.86～1.03之间可组成钙钛矿结构，当t=1时，体系为理想钙钛矿结构。常见的钙钛矿氧化物材料有KNbO3、BaTiO3、LaAlO3等。

另一方面，近年来，2p轻元素掺杂氧化物产生了铁磁性，由于其磁性起源不同于传统的铁磁性材料而成为凝聚态物理领域研究热点[2-9]。科学家们对C、N、B等轻元素掺杂二元氧化物ZnO进行了大量研究。Pan等[2]制备了C掺杂ZnO薄膜，发现该薄膜具有室温铁磁性，理论计算表明磁性起源于锌原子与碳原子之间的电子交换。Xu等[10]研究发现B元素掺杂ZnO体系同样具有室温铁磁性，但是将磁性归结为B和Zn最邻近的O原子的p电子。Shen等[11]研究了N掺杂ZnO的磁性，将其归结为N原子p电子和O原子p电子间的p-p耦合。Yang等[6]将研究扩展到了具有钙钛矿结构的三元氧化物，并将其磁性归结为掺杂N原子之间的耦合作用。随后，本课题组[12-14]研究发现C和B原子间隙掺杂BaTiO3的磁性源于Ti原子未配对的3d电子自旋极化；C原子替位掺杂BaTiO3的磁性源于C原子未配对的2p电子自旋极化，N原子替位掺杂BaTiO3磁性源于N原子的2p电子与O原子的2p电子的p-p耦合作用，B原子替位掺杂BaTiO3的磁性机制可归结为B原子2p和O原子2p与Ti原子3d电子的p-d耦合作用。本课题组[15]也对另一种钙钛矿氧化物KNbO3的空位磁性进行了研究，发现Nb空位和K空位均有磁性，且磁性起源于O原子的2p电子极化。但是在LaAlO3中，其B位的Al原子的电子组态为3s23p1，没有d电子，2p轻元素掺杂是否可以产生铁磁性？若存在铁磁性，其磁性起源机制是什么？这些都值得探究。基于此，本文采用第一性原理计算N掺杂LaAlO3电子结构，发现N替代LaAlO3中的O原子和位于LaAlO3晶胞间隙均产生铁磁性，其磁性都源于杂质N原子的2p电子与体系价带顶O原子的2p电子间的p-p耦合。

2 理论模型与计算方法

本文计算工作采用VASP软件包[16]完成。计算选取立方相LaAlO3为原胞，然后构建2×2×2的超晶胞作为基本计算模型，如图1(a)所示；本文主要研究了N原子替位、间隙掺杂模型，即N原子替代超胞中的一个O原子和处于超胞的间隙中，分别标记为Nsub-LaAlO3和Nins-LaAlO3，如图1(b)和1(c)所示。首先对构建的计算模型进行了几何结构优化。参与计算的价态电子为：N 2s22p3, La 5d16s2, Al 3s23p1, O 2s22p4。电子与离子实之间的相互作用势采用基于广义梯度近似(GGA)的超软赝势(ultra-soft)[17]和PBE交换关联函数[18]。作用在单个原子上的力小于0.1 eV/Å，平面波截断能量取400 eV。

图1 N掺杂LaAlO3的几何结构 (a)LaAlO3;(b)Nsub-LaAlO3;(c)Nins-LaAlO3 Fig.1 Geometry structure of N-doped LaAlO3 (a)LaAlO3；(b)Nsub-LaAlO3;(c)Nins-LaAlO3

3 结果与讨论

3.1 稳定性分析

生成焓和结合能是判定物质稳定性的重要参数[19-20]，生成焓ΔHf定义为：

ΔHf(LaAlO3)=[Et(LaAlO3)-nLaEbulk(La)-nAlEbulk(Al)-3nOE(O2)/2-nNE(N2)/2]/n

(1)

式中Et(LaAlO3)为掺杂体系的总能量，Ebulk(La) 为稳定La单质的总能量，Ebulk(Al)为稳定Al单质的总能量，E(O2)为一个氧气分子的总能量，E(N2)为一个氮气分子的总能量，nLa、nAl、nO、nN分别为超胞中所含的La、Al、O、N原子个数。计算的生成焓数值如表1所示，发现Nsub-LaAlO3，Nins-LaAlO3体系的生成焓小于零，说明N掺杂LaAlO3体系的结构稳定；而且发现ΔHf(LaAlO3)<ΔHf(Nsub-LaAlO3)<ΔHf(Nins-LaAlO3)<0，说明体系结构稳定性按LaAlO3，Nsub-LaAlO3，Nins-LaAlO3的顺序依次降低。

体系的结合能的定义为[21]:

Eb(LaAlO3)=[Et(LaAlO3)-nLaEisolate(La)-nAlEisolate(Al)-nOEisolate(O)-nNEisolate(N)]/n

(2)

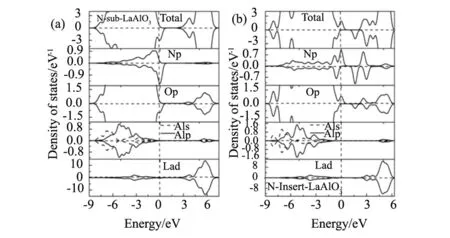
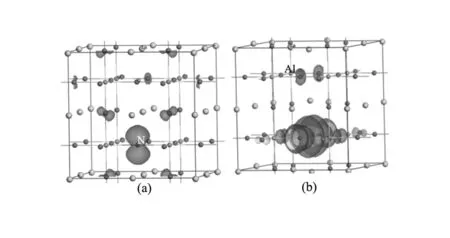
式中Et(LaAlO3)为掺杂体系的总能量，Eisolate(La)为一个La原子的总能量、Eisolate(Al)为一个Al原子的总能量，Eisolate(O)、Eisolate(N)分别为一个O、N原子的总能量，nLa、nAl、nO、nN分别为超胞中所含的La、Al、O、N原子个数。计算的体系结合能数值如表1所示，发现Eb(Nins-LaAlO3)

表1 N掺杂前后LaAlO3的生成焓、结合能和自旋极化能Table 1 Enthalpy of formation, cohesive energy and spin polarization energy of N-doped LaAlO3

3.2 缺陷形成能

为进一步研究N掺杂LaAlO3结构的稳定性，计算了掺杂体系的形成能。对Nsub-LaAlO3模型，其形成能计算公式如下[12,21]：

Eform=Etot(N-doped)-[Etot(pure)+μN-μO]

(3)

对Nins-LaAlO3模型，其形成能计算公式如下：

Eform=Etot(N-doped)-[Etot(pure)+μN]

(4)

式中Etot(N-doped)和Etot(pure)分别为N掺杂后和未掺杂的LaAlO3晶胞总能量， N和O原子的化学势分别为μN和μO。考虑生长条件对形成能的影响，即分别在氧化状态下和还原状态下形成能。在氧化状态下，O原子的化学势取基态氧分子的能量，即μO=μO2/2；对N原子，其化学势取自N的最高稳定化合价的氧化物，即NO2分子与氧分子O2的差值，即μN=μNO2-μO2。在还原状态下，替位掺杂时，考虑到化学方程式：

LaAlO3+(x/2)N2→LaAlO3-xNx+(x/2)O2

(5)

式中的x为掺杂的N原子的个数。所以对O原子，其化学势依然取基态氧分子的能量，即μO=μO2/2。

计算结果如图2所示，表明替位掺杂和间隙掺杂体系在还原状态下的形成能更低，即在还原条件下更能实现N掺入LaAlO3中。且对比替位掺杂的形成能比间隙掺杂的形成能更低，即在制备过程中，N更多以替位而非间隙形式存在。

图2 N掺杂LaAlO3的形成能 Fig.2 Formation energy of N-doped LaAlO3

图3 不同N源掺杂LaAlO3的形成能 Fig.3 Formation energy of doped LaAlO3 with different N source

基于以上结论，继续探讨不同的N源对掺杂的影响。分别以NH3和N2为N源时，替位掺杂时形成能计算方程式分别为：

LaAlO3+(x/2)N2→LaAlO3-xNx+(x/2)O2

(6)

LaAlO3+x(NH3)→LaAlO3-xNx+xH2O+(x/2)H2

(7)

定义以NH3和N2为N源时，间隙掺杂时形成能计算方程式分别为：

LaAlO3+(x/2)N2→LaAlO3Nx

(8)

LaAlO3+x(NH3)→LaAlO3Nx+(3x/2)H2

(9)

其中x为氮源的个数，计算结果如图3所示，表明对替位掺杂而言，NH3源的形成能更低，更容易掺杂；对间隙掺杂而言，N2源的形成能更低，更容易形成掺杂。综上，发现以NH3为N源制备的N替位掺杂LaAlO3的形成能最低，最易合成LaAlO3-xNx。

3.3 电子结构

Nsub-LaAlO3体系和Nins-LaAlO3体系的总态密度(DOS)以及La、Al、O、N原子的分波态密度(PDOS)如图4所示。从图4(a)看出，在Nsub-LaAlO3体系中能量E=0即费米面附近自旋向上和自旋向下的态密度不相等，具有明显的劈裂现象，说明Nsub-LaAlO3体系中对外表现出净磁矩，呈现铁磁性。从分波态密度图可发现N原子的2p电子态与O原子的2p电子态在费米面附近具有明显的重叠现象，说明N-2p电子态与O-2p电子态产生了杂化，形成共价键，该杂化耦合作用导致费米面附近的能级退简并，从而使得能量E=0附近的自旋向上和自旋向下的态密度不相等，Nsub-LaAlO3体系因此产生铁磁性；即Nsub-LaAlO3体系的铁磁性源于杂质N原子的2p电子与价带顶O原子的2p电子间的类似p-d耦合的p-p耦合作用。一个氮原子替位一个氧原子产生的总磁矩为1.00 μB，相应的自旋电子密度分布图如图5(a)所示。

从图4(b)看出，在Nins-LaAlO3体系中，同样地，在费米面附近自旋向上和自旋向下的态密度不相等，具有明显的劈裂现象，说明Nins-LaAlO3体系中电子间的耦合作用使得自旋排列出现有序，体系对外表现出净磁矩，呈现铁磁性。同样从分波态密度图也可发现自旋密度局域在掺杂的N离子本身以及邻近的O原子上，说明Nins-LaAlO3体系的磁矩可归结为N-2p电子态与O-2p电子态间的耦合作用。由于LaAlO3体系的价带顶部由O-2p态电子构成，而杂质N-2p电子态的对称性以及波函数均与O-2p电子类似，所以在费米面附近O-2p和N-2p电子态会发生p-p耦合，使得2p轨道分裂，进而使得自旋向上和自旋向下的态密度不相等，体系产生铁磁性。每个N原子间隙掺杂产生1.00 μB的总磁矩，相应的自旋电子密度分布图如图5(b)所示。

图4 N掺杂LaAlO3体系的电子总态密度及部分原子的分波态密度图 (a)N替位掺杂LaAlO3;(b)N间隙掺杂LaAlO3 Fig.4 Total and partial density of states of N-doped LaAlO3(a)Nsub-LaAlO3;(b)Nins-LaAlO3

图5 N掺杂LaAlO3体系的自旋电子密度分布图 (a)N替位掺杂LaAlO3;(b)N间隙掺杂LaAlO3 Fig.5 Spin electron density distribution of N-doped LaAlO3 (a)Nsub-LaAlO3;(b)Nins-LaAlO3

4 结 论

采用第一性原理计算方法，研究了Nsub-LaAlO3和Nins-LaAlO3的稳定性和电子结构，发现二者都具有稳定的结构，且Nsub-LaAlO3稳定性比Nins-LaAlO3更高；形成能表明在还原条件下，Nsub-LaAlO3比Nins-LaAlO3更容易制备。电子结构表明Nsub-LaAlO3和Nins-LaAlO3体系均具有铁磁性，其磁性均源于杂质N原子2p电子与价带顶O原子2p电子间的p-p耦合，计算结果给制备铁磁性LaAlO3氧化物材料提供了理论指导。