一道高考选择题的多种解法
2019-02-15魏艺铭
数理化解题研究 2019年1期
魏艺铭
(北京工业大学附属中学 100022)
题目设x、y、z为正数,且2x=3y=5z,则( ).
A.2x<3y<5zB.5z<2x<3y
C.3y<5z<2xD.3y<2x<5z
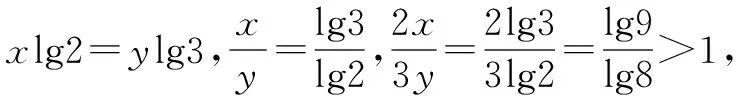
综上,3y<2x<5z.
点评已知条件2x=3y=5z相当于三个等式,首先利用2x=3y去比较2x与3y的大小关系,这类指数问题经常转换为对数,因此将2x=3y两边取常用对数得到x与y的关系,比较大小常用比差法或比商法,根据式子的结构我们感觉更适合用比商法.然后再利用2x=5z,类似地得到了2x与5z大小关系,法1是此类问题的基本解法.
解法2 令2x=3y=5z=k,则x=log2k,y=log3k,z=log5k.

综上3y<2x<5z.
点评对于等式2x=3y=5z,常常令它们都等于k,用指对数的互化把x,y,z都用k表示出来,再用比商法,但在解题过程中为了消掉k,用到了换底公式.
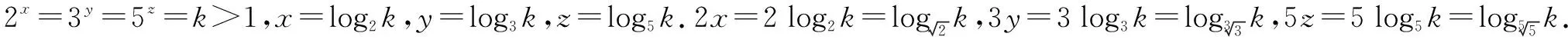
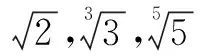
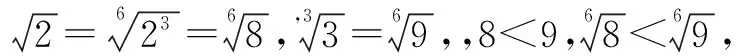
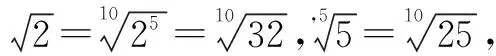

点评解法3一开始与解法2一样,后面用了换底公式的推论把2x,3y,5z表示成了底数不同真数相同的对数,根据同一坐标系中不同对数函数之间图象的位置关系,只需比较三个底数之间的大小关系.这种统一很重要,为我们比较大小提供了一个切实可行的思路.
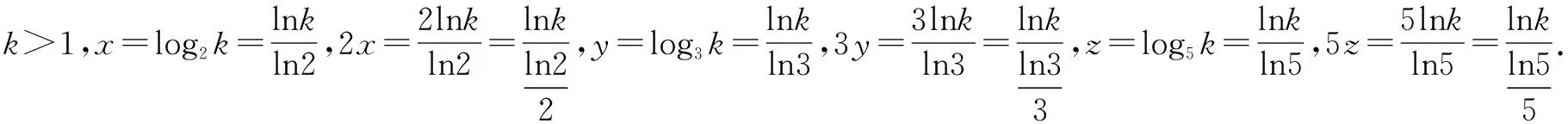
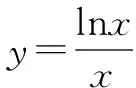
当x∈(e,+)时y′<0,函数单调递减.
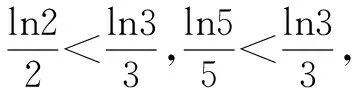
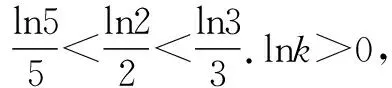
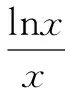
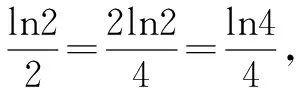
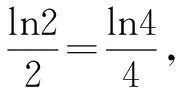
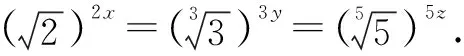
点评前5种解法的共性是都转化成了对数,相比而言解法6把已知条件稍加变形,只用了指数函数的相关性质,可谓简单!漂亮!
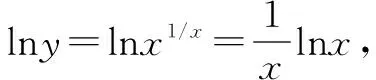
y′=xx-2(1-lnx),当x∈(e,+)时y′<0,函数y=x1/x单调递减.
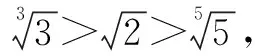
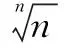
对于一道高考试题,应注重发挥其一题多解背景下的功能与价值,以期达到最小的投入,最大的产出,这样日积月累,同学们的解题意识和能力自然会得到提高.