高考题中解答存在漏洞的四道题
2019-02-15武增明
武增明
(云南省玉溪第一中学 653100)
试题1 (2017年高考全国Ⅲ卷文科数学第19题)如图,四面体ABCD中,△ABC是正三角形,AD=CD.

(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
为了方便表述,现把命题者(官方)给出的解答照录如下:
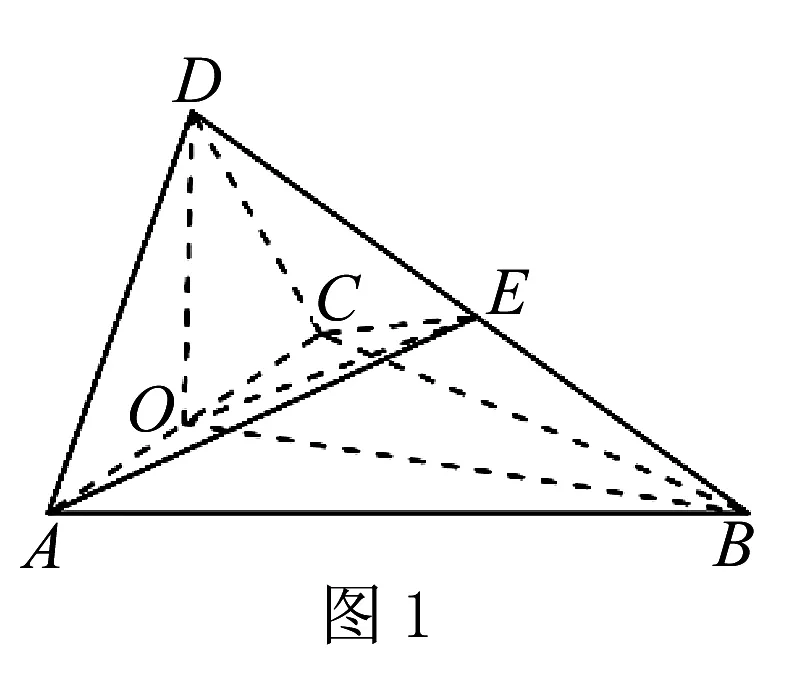
解(1)取AC的中点O,连接DO,BO,如图1.
因为AD=CD,所以AC⊥DO.
又由于△ABC是正三角形,所以AC⊥BO.
从而AC⊥平面DOB,故AC⊥BD.
(2)连接EO.
由(1)及题设知∠ADC=90°,所以DO=AO.
在Rt△AOB中,BO2+AO2=AB2.
又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.


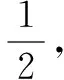
上述解答,漏洞在哪里?漏在哪一步?漏什么?我们先看下面的结论1.
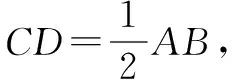
证明方法1(解析几何法) 以直角顶点C为原点,边CA所在直线为x轴,建立平面直角坐标系,如图2.


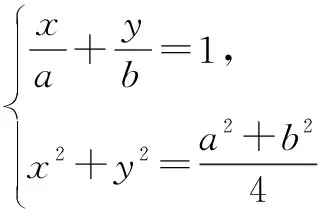
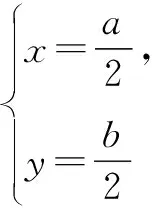
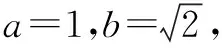


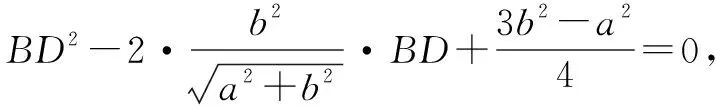
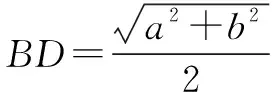
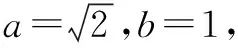
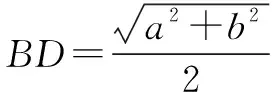


方法3(几何画板法) 借助几何画板,可画出如图3的图,由图直观看到,点D不一定是斜边AB的中点.

漏什么?这个漏洞怎么补?我们先看下面的结论2.




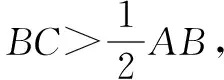
此结论通过作图,如图4,观察图形就可理解.
由上述结论2我们可看出,上述高考题的解答,漏了说明OB与OD的关系式或OB与AB的关系式或OD与AB的关系式这个条件.
这个漏洞可以说是很严重的,甚至致使了解答上的错误,也很容易误导学生.当然这也许是命题者的疏忽,但是由于数学是一门非常严谨的自然科学,所以我们都要引以为戒!
许多学生和老师都认为这道高考题是道容易题,笔者认为是道难题,难在不容易严谨地判断出E是BD的中点.这种观点,可能命题者不同意,也可能命题者在命制这道高考题时,没有意识到严格地判断出E是BD的中点确实不容易.
试题2 (2017年高考北京卷文科数学第15题)已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5.
(1)求{an}的通项公式;
(2)求和:b1+b3+b5+…+b2n-1.
为了方便表述,现把命题者(官方)给出的解答照录如下:
解(1)设等差数列{an}的公差为d,
因为a2+a4=10,所以2a1+4d=10,解得d=2.
所以an=2n-1.
(2)设等比数列{bn}的公比为q,
因为b2b4=a5,所以b1qb1q3=9,解得q2=3.
所以b2n-1=b1q2n-2=3n-1,
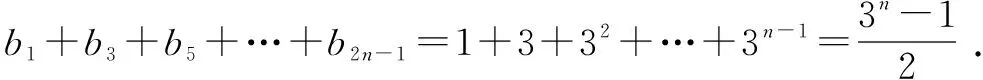

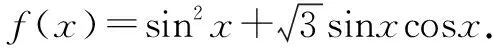
(1)求f(x)的最小正周期;
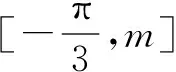
为了方便表述,现把命题者(官方)给出的解答照录如下:

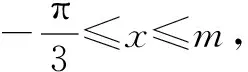

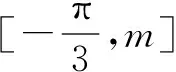
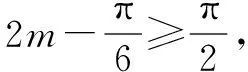
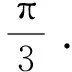



为了方便表述,现把命题者(官方)给出的解答照录如下:
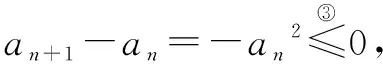
由an=(1-an-1)an-1,得an=(1-an-1)(1-an-2)…(1-a1)a1>0.
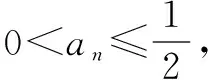
所以Sn=a1-an+1, ①
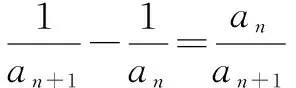
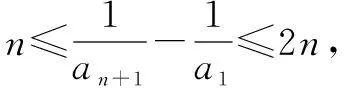


命题者(官方)给出的解答过程中,有三处漏洞,甚至可以说是有三处错误,第一、二处漏洞是③处、④处的等号不应该有,否则an+1=an=0.第三处漏洞是⑤处不应该是“闭”,否则an=0.
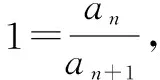
另外,笔者有一些不成熟想法:虽然在证明不等式时,可以不考虑等号成立的条件,再说,“3>2”可以改写为“3≥2”,“3=3”可以改写为“3≥3”,但是由于数学是一门非常严谨的自然科学,所以我们在教学过程和学习数学的过程中都会很自然地想到等号成立的条件.在此高考试题的第(1)问和第(2)问待证不等式左边的等号既然不成立,这个等号就不要加上去了,否则会误导考生,甚至会影响考生的前途和命运.