用解析法求解蟑螂的速度范围

黄俊威 杨承翰 张至佳

(湖北省武市汉黄陂区第一中学 430300)

杨承翰(2001.11-)，男，在校学生.

张至佳(2001.2-)，男，在校学生.

题目一只蟑螂和两只甲壳虫在一个水平大桌面上爬行，每只甲壳虫的速度都能达到1cm/s，开始时，这些虫子恰好位于一个等边三角形的三个顶点上，问蟑螂应具备什么样的速度才能在两只甲壳虫任意移动的情况下仍能保持三者分别位于一等边三角形的三个顶点上？

解析首先，假设第一只甲壳虫A1不动，在时间Δt内，第二只甲壳虫A2爬行了S2，要保持蟑螂和两中甲壳虫在变化后的等边三角形的三个顶点上，为协调这一关系，由图1可知，蟑螂移动了TT′=S2=v1Δt.其次，再假设第二只甲壳虫A2不动，同样在时间Δt内，第一只甲壳虫A1爬行了S1，则蟑螂移动了T′T″=S1=v1Δt.

上述两只甲壳虫的运动是独立的，它们的位移是各自产生的，是遵循矢量的独立原理.同时，矢量也是满足叠加原理的，我们完全可以想象两只甲壳虫的运动同时进行的，而蟑螂是分别协调关系的，即将两个独立的运动协调关系叠加，则由图2可得蟑螂同时满足两只甲壳虫随意运动的位移协调关系为：TT″=TT′+T′T″.同时由图2的矢量关系

可知;TT″≤TT′+T′T″=(v1+v2)Δt,则v0≤v1+v2=2v=2 cm/s.

即蟑螂必须具备可达到2 cm/s的速度才能保证三者分别位于一等边三角形的三个顶点上.

笔者认为以上的分析表面看起来天衣无缝，但是不是两只甲壳虫的速度同向时蟑螂有最大速度吗？两只甲壳虫速度方向相反时蟑螂有最小速度吗？

正解解析

1.建立模型

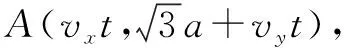
B(-a+v1cosθ·t,v1sinθ·t),

C(a+v2cosα·t,v1sinα·t)

2.方程的求解

由于三只昆虫始终组成一个正三角形，则AB=AC=BC，即

解方程后得

蟑螂的速度方向与水平方向所成的角为

3.讨论

(1)当θ-α=2π/3时，蟑螂的速度有最大值v1+v2

(2)当α-θ=π/3时，蟑螂的速度有最小值|v1-v2|

如图4所示，当两只甲壳虫的速度方向夹角为120度时，蟑螂的速度有最大值.

如图5所示，当两只甲壳虫的速度方向夹角为60度时，蟑螂的速度有最小值.

综上所述，蟑螂的速度范围是v∈[|v1-v2|,v1+v2]