到定点与定直线的距离差为定值的点的轨迹的探究
2019-02-15商轶玮
商轶玮
(上海市北虹高级中学 200080)
一、提出问题
例题(沪教版高二下第12.7节) 动点P(x,y)到定点F(2,0)的距离比它到定直线x+4=0距离小2,求动点P(x,y)的轨迹方程.
变式动点P(x,y)到定点F(2,0)的距离比它到y轴的距离大2,求动点P(x,y)的轨迹方程.
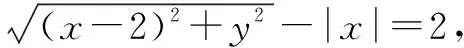
反思经历了上述的错误,很多同学再遇到类似的问题时,难免困惑——到定点与定直线的距离的差为定值的动点的轨迹到底是什么?何时才是一条抛物线?
二、探究过程
我们可以从“数”与“形”两个角度来进行分析.
1.几何方法:不妨设动点P到定点F的距离为d1,到定直线l的距离为d2,定点F到定直线l的距离为d.
当d1=d2时,由抛物线定义可知,点P的轨迹是一条抛物线(F∉l);或是一条过点F且垂直于l的直线(F∈l).
当d1
(1)若t
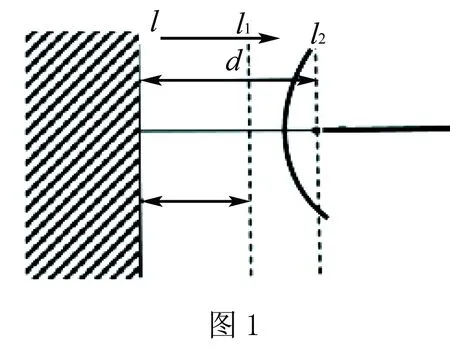
(2)若t=d,如图1,可将直线l向右平移t个单位至直线l2,即动点P到点F和直线l2的距离相等,所以动点P的轨迹就是以为定点F为端点一条垂直于l2的射线(方向向右)
(3)若t>d2,若将直线l向右平移t个单位,则“越过”了定点F,显然不成立,故动点P的轨迹不存在.
当d1>d2时,令d1-d2=t(t>0).
(1)若t
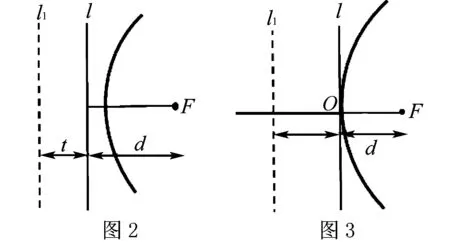
(2)若t=d,如图3,此时动点P的轨迹既可以出现在直线l的右侧,又可以出现在直线l的左侧.直线l右侧的轨迹可将直线l向左平移t个单位至直线l1,所以在直线l的右侧动点P的轨迹就是以点F为焦点,以l1为准线的一条抛物线(顶点为O).显然,直线l左侧的轨迹是一条以O为端点的向左的射线.综上所述,动点P的轨迹是一条抛物线加上一条射线.
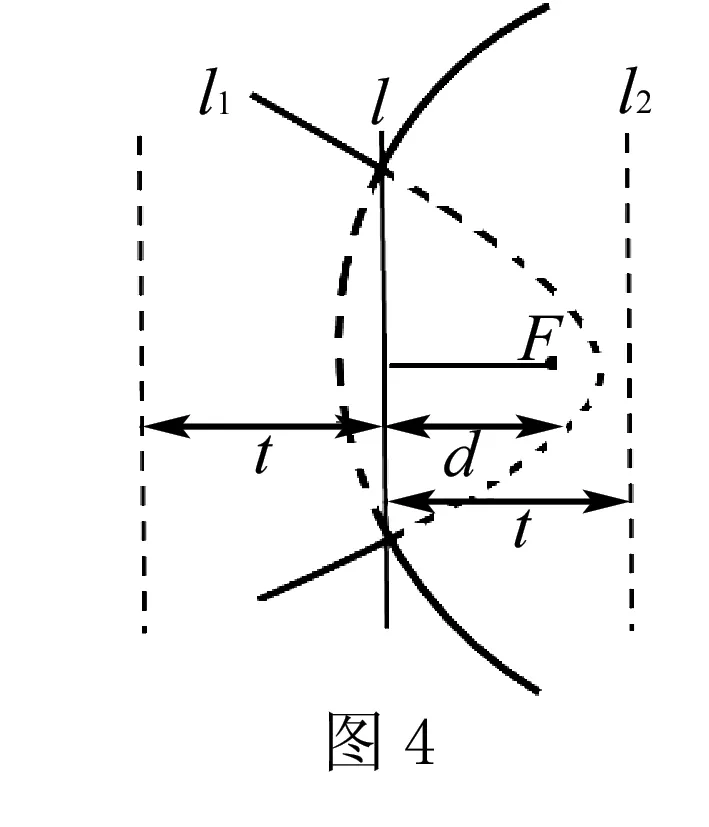
(3)若t>d,如图4,此时动点P的轨迹既可以出现在直线l的右侧,又可以出现在直线l的左侧.对于直线l右侧的轨迹,可以将直线l向左平移t个单位至直线l1,所以动点P的轨迹就是以点F为焦点,以l1为准线的抛物线在直线l右边的部分;同样对于直线l左侧的轨迹,可以将直线l向右平移t个单位至直线l2,所以动点P的轨迹就是以点F为焦点,以l2为准线的抛物线在直线l左边的部分.
综上所述,动点P的轨迹是两条抛物线各取一部分.
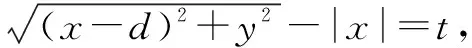
两边平方并化简得,y2=t2-d2+2dx+2t|x|,即y2=
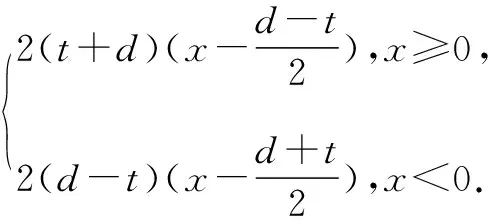
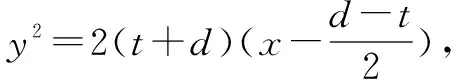
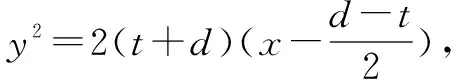
三、一般结论
1.通过以上探究过程,不难发现,平面内到定点与定直线的距离的差为定值的动点的轨迹大致分为三类八种情况.
2.可以归纳出,定值t当且仅当-d
3.抛物线定义的推论:平面内到定点F与定直线l(F∉l,F到l的距离为d)的距离的差为常数t(|t|