浅析整体法和隔离法在高中物理习题求解中的应用
2019-02-15宋惠龙
宋惠龙
(湖南省醴陵市第一中学 412200)
一、隔离法与整体法的基本内涵
在习题求解过程中将研究对象聚焦到“部分”之中,将其从系统之中“隔离”出来进行单独的研究和分析,即为隔离法.整体法则是将研究的对象定位于整体上并对相关的规律进行思考与研究.在高中物理习题求解过程中整体法与隔离法充分地贯穿其中,在动量能量、连接体以及静力学等物理习题的求解中有着广泛应用.在运用中需要把握好三个核心的问题:一个是方法的选用及研究对象的确定;一个是两种方法在习题求解中的应用顺序;再一个就是受力分析方法的恰当运用.
二、在物理习题求解中隔离法与整体法应用的思维方法
1.应用于平衡状态类习题求解
如图1所示:有两个物体,其质量分别为m1和m2,它们以轻质弹簧为媒介互相连接,对物体施加F力,此时m1和m2两个物体均沿着水平方向进行匀速直线运动,其中m2处于空中状态,而m1则是位于地面之上,F力与水平方向之间的夹角为θ,需要求解的问题是m1所受到的摩擦力f与支持力FN是?
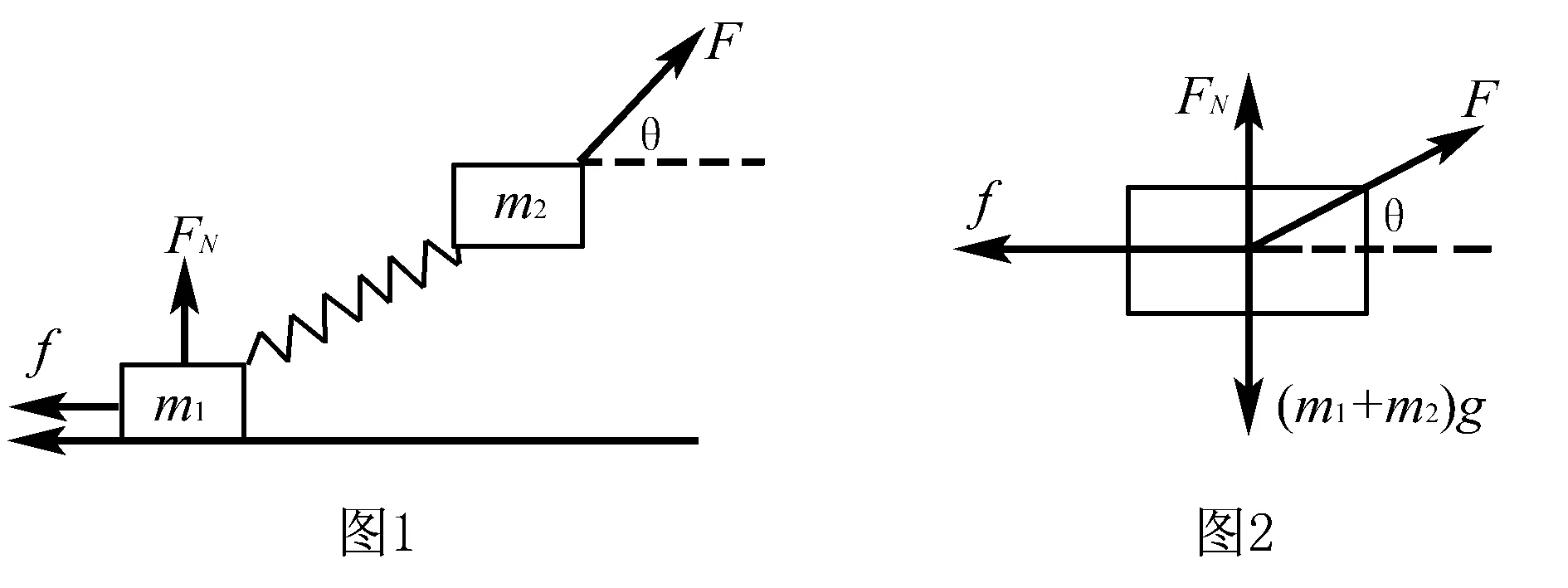
在该问题的思考中,可以将m1、m2及其他们的连接媒介弹簧作为一个整体来看待,m1和m2两个物体所受到的弹簧力属于内力的范畴,因此可以忽略不计.那么就可以对这一整体所收到的外部作用力进行分析,如图2所示,那么就可以分别从竖直和水平两个方向列方程,即:f=Fcosθ
FN+Fsinθ=m1g+m2g-Fsinθ
求解上述方程:
F=Fcosθ
FN=m1g+m2g-Fsinθ
在这一物理习题的求解过程中如果选择隔离法则需要对于m1和m2两个物体分别受到的力进行分析,在列方程的过程中也需要分别列,这样就会让问题的过程变得复杂,列的方程不仅比较多,而且极为繁琐,而运用整体法则实现了问题的简单求解.
2.应用于牛顿定律类问题求解
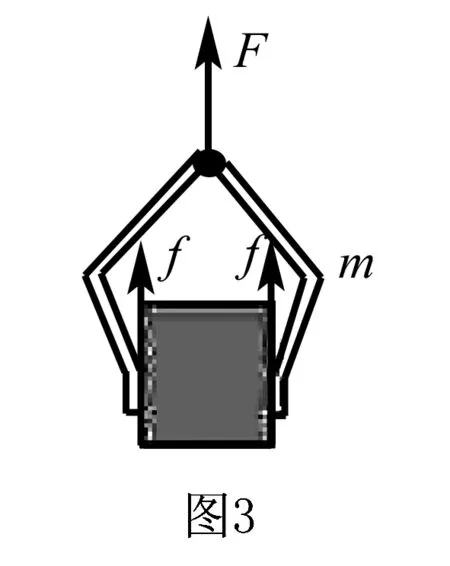
如图3所示,用一个带有弹簧的夹子将木块固定住,通过外力F力的施加将木块拉起来,假定夹子的质量为m,木块的质量为M,木块和夹子的连接部分两侧都受到静摩擦力f力的影响,如果木块在上升的过程之中保持不滑动的状态,需要求解的问题是F的最大值.
此问题中可以首先将小木块拿出来作为一个部分看待,那么在小木块的受力分析中运用隔离法可以得到:2f-Mg=Ma,此时求得的木块的最大加速度为a=2f/M-g.
同时,还需要对木块和夹子构成的整体进行力的分析,由此可以得出F-(M+m)g=(M+m)a,通过计算得到F=2f(M+m)/M.
在这一习题的求解过程中先后运用了隔离法与整体法,分别将小木块作为部分、小木块与夹子作为整体进行研究对象的精准确定.
3.应用于非平衡状态类问题求解
如图4所示:将一个木箱子置于地面上,该木箱子质量为M,木箱上方有一拉杆,一小球套于拉杆上,其质量为m,从拉杆的顶部将处于静止状态的小球释放下来,小球自然地沿着立杆下滑,保持0.4g的加速度,需要求解的问题是:小球在向下滑落时,求木箱子对于地面的压力?
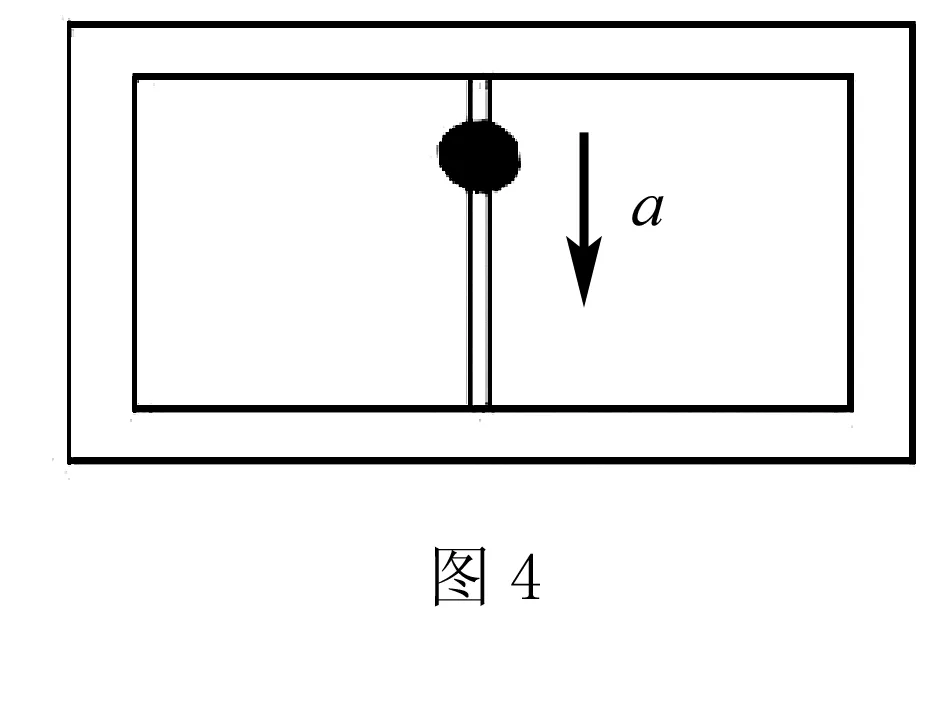
可以将研究内容聚焦于小球,并对其受力进行分析,小球受力包含:向上摩擦力f和向下重力mg.借助牛顿第二定律原理我们可以得出:mg-f=ma=0.4mg,推导出f=0.6mg.再将研究对象定位于木箱上,并对其受力进行分析,可得知,木箱总共受到三个力的作用,即:地面支撑力F、小球对木箱向下的摩擦力f2和重力Mg,此时木箱处于静止状态.通过牛顿第二、第三定律分别得出
F=Mg+f2
F2=f
F=Mg+0.6mg
同时,还可以将研究对象定位于小球和木箱这一整
体上,并对其受力进行分析,此时系统小球和木箱所受到的作用力包括两个方面:一个是地面对木箱的支持力F,另一个则是系统所受到的重力(M+m)g.
通过牛顿第二定律可以求得:
(M+m)g-F=ma=0.4mg
经计算得到:F=Mg+0.6mg
该题目中所涉及到两个物体,因此隔离法应用并不复杂,但当涉及到3个及其以上的物体时,并且涉及到的物体保持不同的加速度时,则整体法的运用更为适宜.
综上,在物理习题中涉及到多个运用过程的组合或者多个物体相互作用的情况之下,应当选择隔离法或者整体法进行习题的求解,在运用过程中要充分结合题目的具体情况进行研究对象的选择和运用方法的实施.