如何利用函数的单调性解题
2019-02-15庞宇轩
庞宇轩
(山东省青岛第二中学 266100)
一、函数单调性的概念
1.函数单调性的概念
在函数f(x)中,假设f(x)中存在两个自变量x1和x2且两个自变量在区间V中,区间V在函数的定义域里,如果x1小于x2时,有f(x1)大于f(x2),就说明函数f(x)在区间V上是单调减函数;反之如果x1小于x2时,有f(x1)小于f(x2),就说明函数f(x)在区间V上是单调增函数.
在研究函数的单调性时一定要在相应的定义域中讨论,如果题目中没有给出明确的区间和区间单调性,此时求解函数的单调性就没有意义.
2.利用函数单调性的概念解题
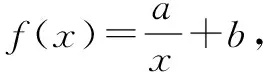
分析由题意可知,x不等于0,因此该函数的定义域是负无穷到0和0到正无穷的并集.
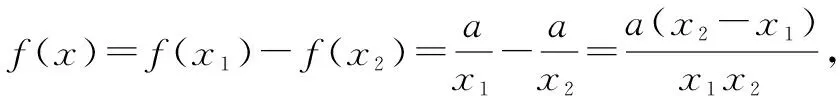
当a<0时,仿照上述方法可得f(x)在(-∞,0)和(0,+∞)内分别是单调递增的.
二、函数单调性的不同解题方法
高中数学在函数单调性这一模块中主要的研究方法有:函数单调性的定义、导数的应用、复合函数的研究以及数形结合的方法.
函数定义:用这种方法做题一般是三个步骤,首先要在相应的单调区间中分别设定两个不同的自变量;其次用两个因变量来比较大小,确定两个因变量的大小关系;最后运用函数单调性的定义在区间下得出结论.
复合函数求解:判断复合函数的单调性首先应该确定定义域下,内外层函数的函数单调性,然后应用复合函数单调性的复合法则来进行判定,在定义区间下,如果内外函数的单调性相同,复合函数是单调增;相反的如果内外函数的单调性不相同,复合函数是单调减.
数形结合:图象是解决函数问题时比较常用的方法之一,利用图象进行观察,可以使问题变得更加直观简单.学生熟练掌握各种基本函数的具体图象和其特点后,就可以直接通过对函数图象的分析去解决相关问题.观察函数的图象,当自变量不断变大时,此区间中该函数的函数值是不断增加的,那么说明该函数在该区间内是单调递增的;同理,如果自变量不断变大,区间中该函数的函数值是不断减少的,那么说明该函数在该区间内是单调递减的.图形的对称性也是解题的关键点,学生可以利用两个函数的对称性和函数自身的对称性来研究函数的单调性.无论如何学生学习这一部分内容都需要认真观察熟练掌握.
三、解决一些实际问题
1.求值
例1 设x,y为实数,且满足
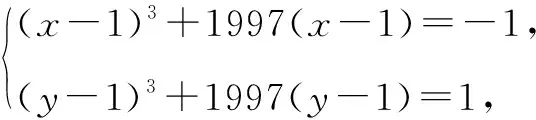
解由已知条件,可得:
故若设f(t)=t3+1997t,则上述条件即为:f(x-1)=f(1-y)=-1.
又易知函数f(t)=t3+1997t在R上是单调增函数,所以由上式有:x-1=1-y,即x+y=2.
2.解方程
例2 解方程(5x+3)3+x3+6x+3=0.
解原方程变为:(5x+3)3+(5x+3)=-(x3+x).
设f(x)=x3+x,则原方程即为:f(5x+3)=-f(x).又f(-x)=-f(x),从而原方程即为:f(5x+3)=-f(x).
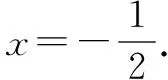
3.求最值
例3 已知点B(0,6),C(0,2),试在x轴正半轴上求一点A,使得∠BAC最大.
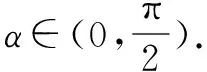
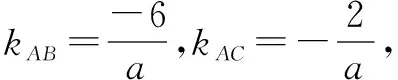
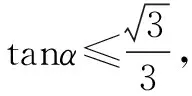
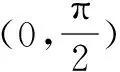
4.比较大小
例4 已知a>1,且ax-logay>ay-logax,试比较x,y的大小.
解由条件得:ax+logax>ay+logay.
引入函数f(t)=at+logat,则上式即为:f(x)>f(y).
易知函数f(t)=at+logat在(0,+∞)上是增函数,所以x>y.
5.证明不等式
例5 设a∈R,求证:a8-a5+a2-a+1>0.
证明当a≤0或a=1时,不等式显然成立.
当a>1时,函数y=ax在R上是增函数,所以a8>a5,a2>a,所以a8-a5+a2-a+1>0;
当0
所以a8-a5+a2-a+1>0.
故对一切a∈R,不等式a8-a5+a2-a+1>0成立.
6.求参数范围
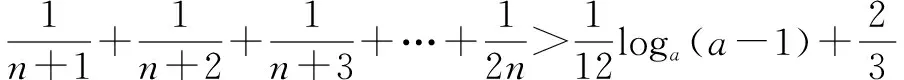
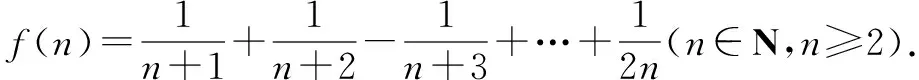
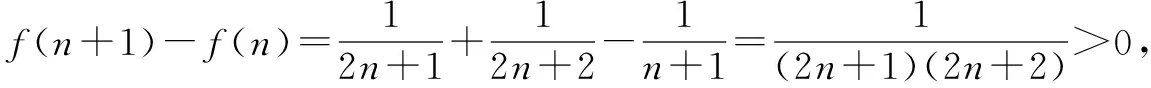
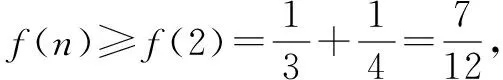
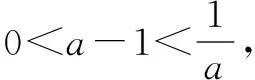
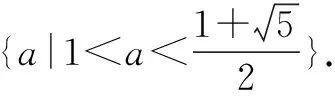
例7 设函数
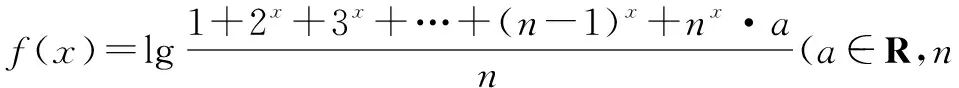


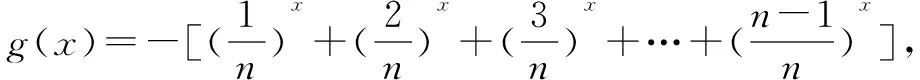
7.解不等式
例8 函数f(x)对任意a、b∈R,都有f(a+b)=f(a)+f(b)-1,且当x>0时,f(x)>1.若f(a)=5,解不等式f(3m2-m-2)<3.
解析可以先根据单调性的定义来判定函数f(a+b)=f(a)+f(b)-1的单调性.
任取实数x1,x2,设x1
f(x2)=f(x1+x)=f(x1)+f(x)-1>f(x1).
所以f(x)在R上是增函数.
由f(4)=f(2)+f(2)-1=5,得到f(2)=3.所以f(3m2-m-2)<3=f(2).

运用函数的单调性解不等式,要注意该函数的定义域,要明确相应定义域上的函数单调性,不然的话在做题过程中很容易出错.
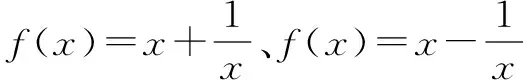
同时,在判断函数单调性的过程中还可以通过观察函数图象的奇偶性的方法来进行.如果函数是奇函数,那么以原点为中心,关于原点对称的区间内该函数的单调性相同;如果函数是偶函数,那么关于原点对称的区间内该函数的单调性相反.
总之,函数知识一直是高中数学教学过程的重点和难点,函数知识的有效学习对于学生未来数学知识的学习过程具有重要的地位. 因此,加强高中函数知识的教学是十分必要的.充分掌握函数单调性的知识可以帮助学生更好地解决不等式,例如参数的不断建立和方程参数的范围.因此,掌握函数的单调知识是非常重要的.