铣刀盘激光熔覆修复过程的温度场与应力场有限元仿真

2019-02-15舒林森王家胜

中国机械工程 2019年1期

舒林森王家胜

1.陕西理工大学机械工程学院，汉中，7230012.陕西省工业自动化重点实验室，汉中，723001

0 引言

目前，数控铣床和铣削加工中心为了缩短换刀时间和保证切削质量，采用“刀片+盘刀”的组合结构替代整体式刀具，但金属高速切削过程产生的冲击、高温和高压等工况容易引起刀具破损失效。刀具破损瞬间使刀具和刀盘上的载荷发生突变，通常会造成刀盘塑性变形而报废。针对此情况，企业要么将损伤刀盘发往原产地维修，要么报废再重新购置新刀具产品。近年来，高能量密度的激光熔覆技术在装备再制造工程中得到推广，激光熔覆对损伤刀盘的再造修复，不仅可实现高效、优质、低成本修复，而且还具有显著的绿色环保效果。基于冶金熔合的激光修复工艺使损伤零件形状、尺寸以及性能得以复原，但也容易在修复部位产生较大的热应力，甚至导致修复部位开裂等问题,因此，铣刀盘激光熔覆修复过程的热-力耦合问题研究就具有重要的研究意义和工程价值。

铣刀盘激光熔覆修复成形机理非常复杂，若控制不当将影响修复后质量，甚至产生缺陷而不能使用。实验表明[1-3]，激光与工件基体、金属粉末直接作用的有限区域内反应剧烈(如：传热、传质、相变以及弹塑性应变等)，工件内部热-力数据即时捕捉难度大、费用高。随着计算机仿真技术的发展，利用有限元法重现铣刀盘激光熔覆修复成形过程，使工件内部的热-力数据即时获取成为可能。CALLEJA等[4]对燃气轮机叶片连续激光熔覆成形过程进行模拟，通过仿真数据对工艺参数进行了优化。张平等[5]采用有限元法，并利用计算软件对比分析，提出了一种激光熔覆热源计算模型。仇卫华等[6]利用ANSYS对激光熔覆过程进行了数值模拟，得到了熔覆层宽度与激光各个参数之间的关系。郭卫等[7]对激光熔覆成形过程中移动高斯热源作用下的温度场进行数值模拟，探讨了扫描速度、激光功率和搭接率等工艺参数对温度场的影响。任会芳等[8]对柴油机曲轴进行激光熔覆修复模拟，确定了激光熔覆过程中的最佳修复材料。贾文鹏等[9]、李德英等[10]仿真模拟了TC4钛合金和SiC/316L复合涂层新材料激光熔覆过程的温度场和应力场分布情况。此外，模拟仿真中的热源模型[11]及各工艺参数选取方法[12-14]也被国内外学者关注。目前尚未见到铣刀盘零件激光熔覆修复及其修复过程温度场及残余应力场分析的文献。

本文首先在分析铣刀盘失效的几何特征基础上建立铣刀盘激光熔覆修复刀盘三维模型，然后对刀盘结构进行有限元网格划分，建立刀盘激光熔覆修复的过程分析模型，通过离散求解获得修复过程的温度场和应力场，最后对该刀盘进行工程实践，进而验证有限元仿真的正确性。

1 铣刀盘修复过程建模

1.1 有限元建模

(a)某失效后的铣刀盘

图1 所示为失效后的某铣刀盘外观形貌及损伤形式。由图1a可见，该铣刀盘能够安装六个刀片，其中刀盘体1号刀片安装位发生了显著的塑性变形(图中圆圈标注位置)，尽管着色检验中未发现其他部位损伤，但该铣刀盘已不能继续使用，必须进行修复处理。为了清晰地表达该刀盘体塑性变形情况，绘制简图进行说明(图1b)。由图1b可以看出，大切削力冲击作用使刀盘体1号刀片支承面发生了不可恢复的挤压塑性变形，其支承平面产生挤压倾斜，材料受挤向外流动，使原有边缘形状向外突出，端部还发生了二次挤压再变形。

(b)铣刀盘损伤形式图1 某失效后的铣刀盘外观形貌及损伤形式简图Fig.1 Appearance and damage form of a milling cutter disk after failure

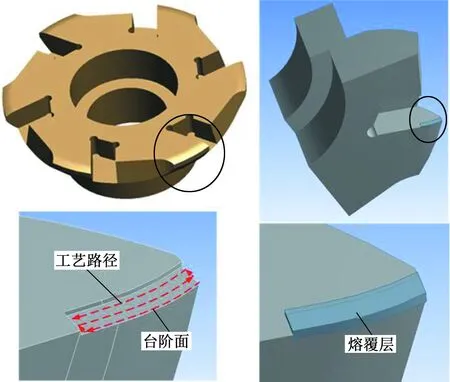
图2 铣刀盘三维几何模型及修复路径Fig.2 Three-dimensional geometric model and repair path of milling cutter disk

为了满足该铣刀盘激光熔覆修复工艺要求，对其进行清洗和铣削台阶等预处理，通过刀盘几何特征点提取得到该铣刀盘的基本形状与尺寸，建立激光熔覆修复铣刀盘的几何模型如图2所示。预处理时在刀盘修复部位加工了台阶面，用于容纳激光熔覆工艺生成的高硬度镍基合金组织。修复过程中金属粉末和激光沿着图中所示的扫描路径进行增材填充，形成的镍基熔覆层比原铣刀盘表面高出0.2 mm，其原因在于激光熔覆修复后的刀盘要达到制造技术的要求和精度还需预留加工余量进行后处理。有限元仿真和后续工程实际采用的激光熔覆过程都采用“弓形”激光扫描工艺路径，既可以保证相邻两次激光扫描的时间间隔较短，又可以使前次扫描的余热成为后次扫描的预热能量，使熔覆深度和宽度增大，熔覆层翘曲变形减小。

本文采用文献[15]的计算域虚拟规划策略及其算法对连续体离散分解，并在修复熔覆层及热影响区进行高密度的局部细化，结果显示，网格模型含六面体HEXA单元20 628个，如图3所示。此外，模型限定网格单元均为规则六面体单元，瞬态热和瞬态结构分析分别用Solid70和Solid185单元，且单元排列与熔覆层形成过程匹配。该模型采用空气自然对流来模拟热边界，以单元生热来模拟激光热源。设基体和熔覆层均满足双线性随动强化模型和屈服准则，并利用“单元生死法”按时序激活来实现金属粉末逐渐沉积的模拟。

激光熔覆修复区域的温度具有高度非线性和时变性，热应力受热循环、基体和粉末材料膨胀率、相变潜热、屈服强度等诸多因素影响，在建立铣刀盘激光熔覆修复过程分析模型时，假设粉末颗粒形状为等尺寸立方六面体，熔覆层表面光整且材料各向同性，忽略熔池金属内流动和压缩性，不计算粉末吹送能耗影响，仅考虑结构张力，计算过程满足准稳态条件。

1.2 过程分析建模

为了更好地逼近激光在熔池中的穿透性，激光熔覆修复过程的热输入采用三维圆锥体热源，其函数为

(1)

式中，q(r,z)为体热流密度；Q为激光能量；η为热转换效率；rj、ri分别为锥体热源顶端半径和底端半径；zj、zi分别为锥体热源深度z的最大值和最小值；r0(z)为关于深度z的热分配系数。

三维非稳态导热微分方程为

(2)

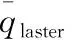
令初始温度为T0，则有始末状态为

(4)

边界条件为

(5)

式中，Ts为边界温度；qs为物体表面的热流密度；Tα为环境温度；h为表面传热系数；nx、ny、nz分别为边界外法线的方向余弦。

根据假设，节点总应变Δε为

Δε=Δεe+Δεp+Δεth

(6)

Δεth=α(T-Tref)

式中，Δεe、Δεp、Δεth分别为弹性应变、塑性应变和热应变；α为线膨胀系数；Tref为参考温度。

节点塑性热应力向量Δσ为

Δσ=Dep(Δεth-Δεp)-Δσ0

(7)

式中，Dep为节点的弹塑性矩阵；Δεth为材料热应变向量；Δεp为弹性应变向量；Δσ0为初始应力向量。

2 分析结果与讨论

2.1 温度场

图4所示为铣刀盘激光熔覆修复成形过程的熔池形态及温度分布。熔池随热源移动而变化，熔池逐渐由半球形演变成彗星形，激光光斑临近区域的温度和温度梯度为非均衡分布。在初始1.2 s内熔池形状不稳定，易导致基体金属熔深不够，需热补偿来满足工艺要求。随后，随着热量累积，熔池的温度达到准稳态，激光照射的修复区域形成稳定的彗星状熔池边界，光斑位置温度达1 690 ℃，熔池边界温度达到1 050 ℃，高于粉末和基体熔点温度，以致于边界透过结合面。值得注意的是，铣刀盘几何边界对熔池形状有明显影响，有可能导致结合边界上的应力突变和塑性变形过大。

(a)t=0.065 s (b)t=1.298 s

(c)t=2.597 s (c)t=3.245 s图4 熔池形态及温度Fig.4 Shape and temperature of molten pool

为了得到铣刀盘上熔覆层与基材的结合状态，按照熔覆层和基体材料层共用单元节点的原则，沿着熔覆路径在修复区域的结合面上选取观测节点N1、N2和N3，其温度-时间历程如图5所示。由图5可见，熔覆层及基体在激光工作时被瞬时熔化(边界节点温度大于1 050 ℃)，激光移开后节点温度快速降低，由曲线可知，结合面的最低温度随着热循环产生的热量累积而升高，循环结束工件急速冷却，最终达到室温。

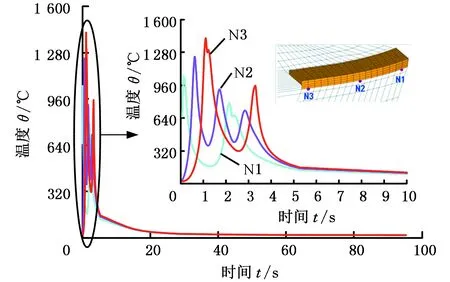
图5 铣刀盘结合界面上的三节点温度-时间历程曲线Fig.5 The temperature-time history curve of threenodes on the interface of the milling cutter disc

图6所示为铣刀盘激光熔覆修复成形过程的温度场，图中，S为步数。由图6可知：①随着激光移动，金属粉末材料在损伤刀盘的基体表面累积，其温度分布也随之改变；②刀盘的基体温度和热影响区随着熔覆过程推进而逐步升高和扩大；③在冷却阶段，模型的熔化区域迅速凝固并快速降温至室温。激光束持续热输入产生能量累积使熔覆层金属和基体温度都得到升高，热传导、对流和辐射使熔覆结束后刀盘迅速进入冷却阶段，激光熔覆加工时间为3.312 s，修复后冷却时间为315.312 s就可达到室温。

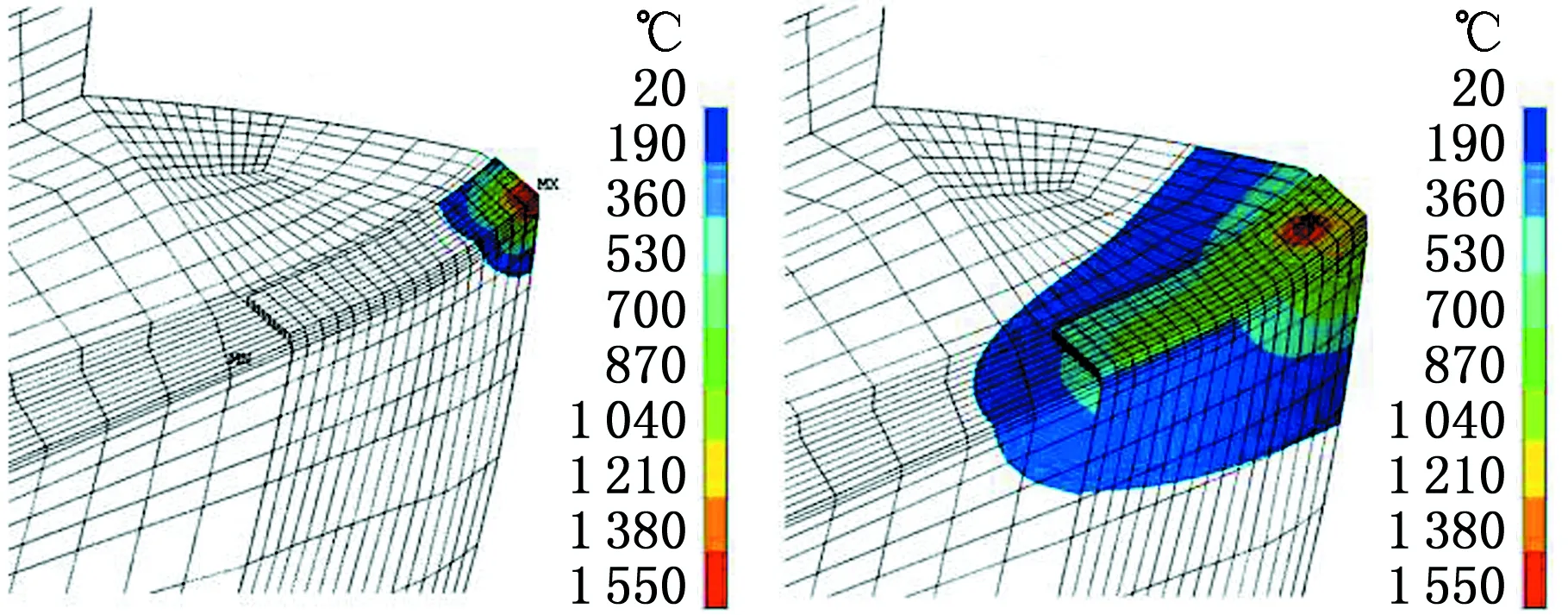
(a)S=1,t=0.065 s(b)S=20,t=1.298 s

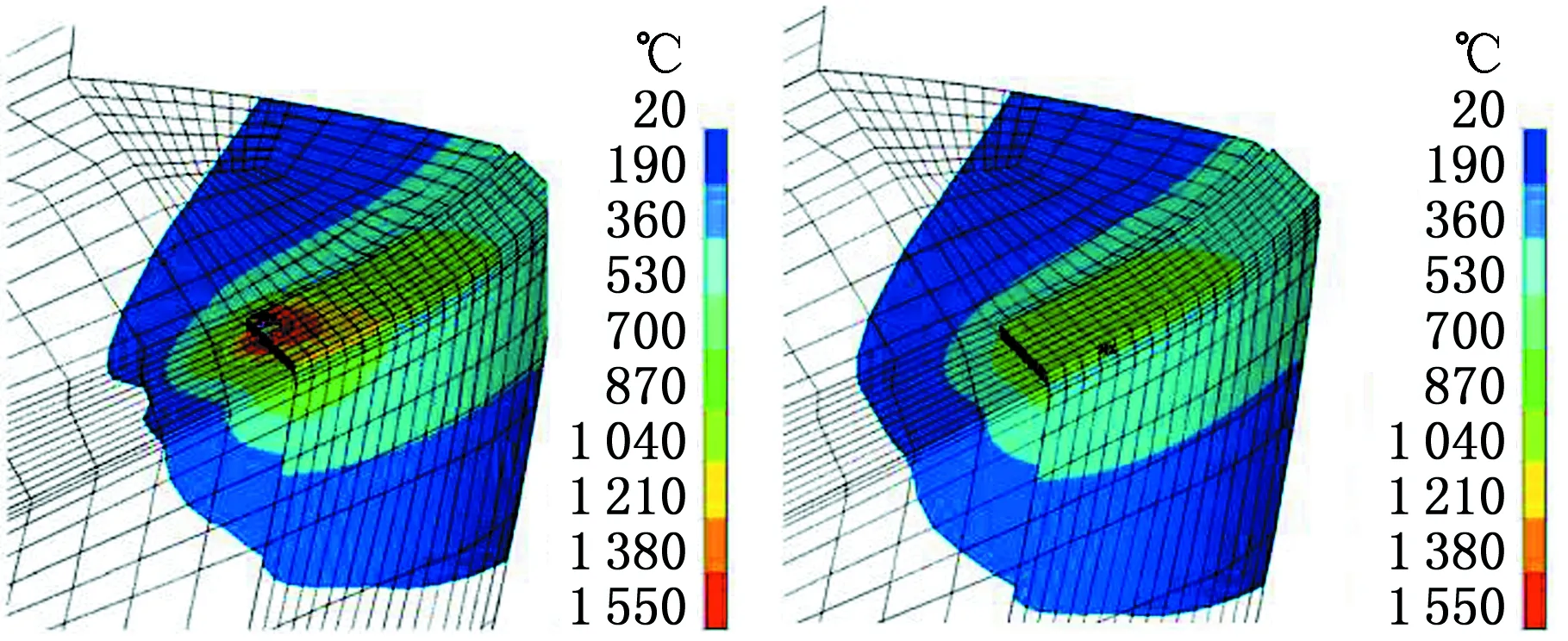
(c)S=51,t=3.312 s(d)S=52,t=3.412 s

(e)S=70,t=5.120 s(f)S=102,t=315.312 s图6 铣刀盘激光熔覆修复过程的温度分布Fig.6 Temperature distribution during laser claddingrepair of milling cutter disk

2.2 应力场

图7为在熔覆层与基材的结合边界上选取的观测节点N1、N2和N3的热应力-时间历程曲线。铣刀盘的激光熔覆修复热应力形成过程复杂，与修复过程激光加热规律相关，加热过程的热应力是不稳定的瞬态应力，材料膨胀和挤压塑性变形同时发生，随着激光远离，节点的热应力历经多个热循环后逐渐稳定到某个数值，整体上表现为初期不稳定且往复变化，随后逐渐稳定形成激光熔覆修复的工艺残余应力，铣刀盘修复后的工艺残余应力为60～200 MPa。

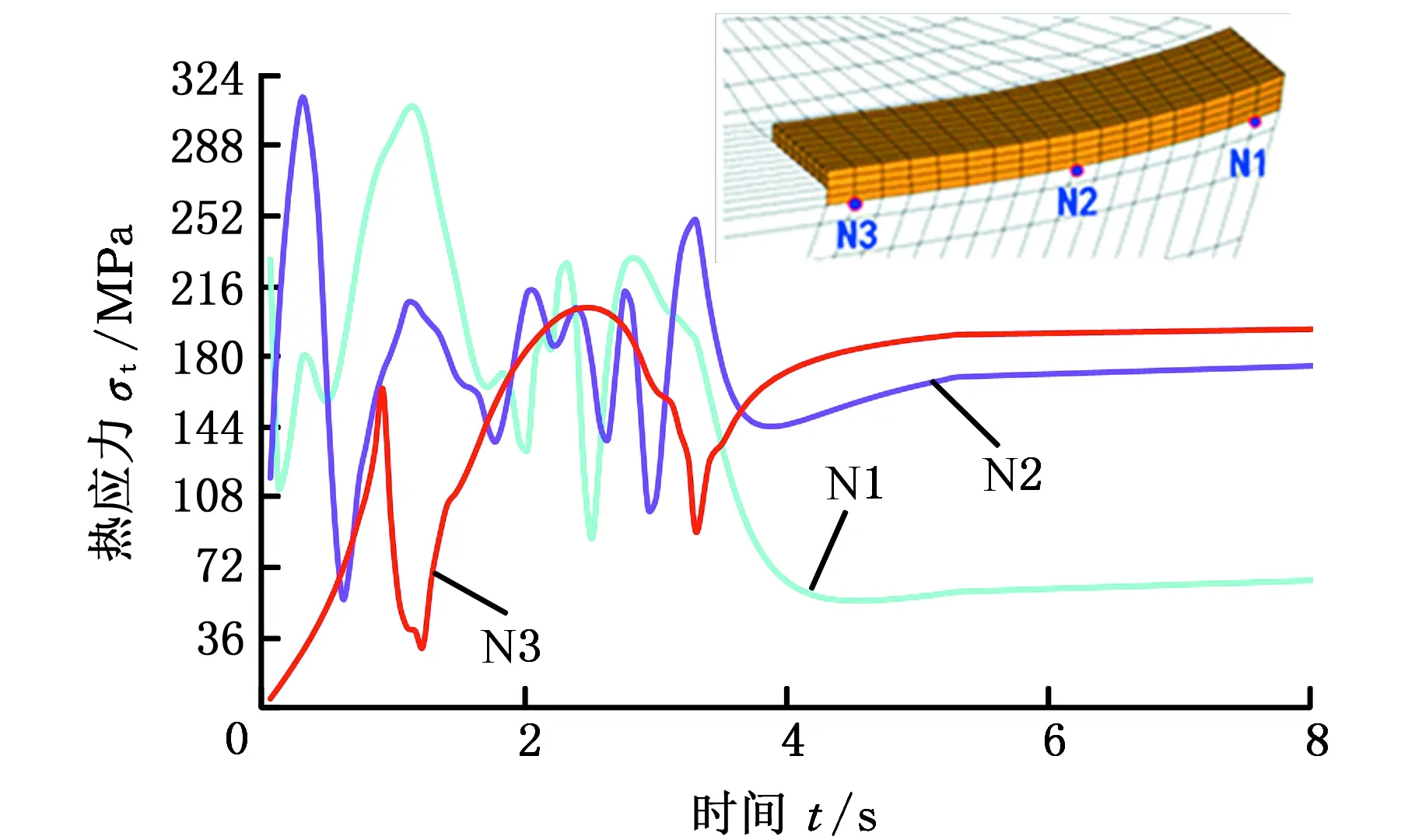
图7 铣刀盘激光熔覆结合面上的三节点等效应力历程Fig.7 Equivalent stress history of three nodes on the interface of milling cutter disc

图8所示为铣刀盘激光熔覆修复加工过程及冷却后的残余应力-应变分布,可以看出，铣刀盘激光修复过程的热应力也是瞬态变化的，热应力随着金属粉末材料在铣刀盘损伤区域的立体堆积逐渐变化。修复过程中，铣刀盘边界上的热应力接近材料的屈服极限，铣刀盘修复结合面处发生了弹塑性变形。冷却后，修复后的铣刀盘熔覆层结合区的残余应力较大，其最大名义应力约为380 MPa，与温度梯度分布基本一致。受几何约束限制，高应力集中在激光修复的熔覆层和铣刀盘的结合位置，最大应力为384 MPa，略低于材料的屈服极限强度。

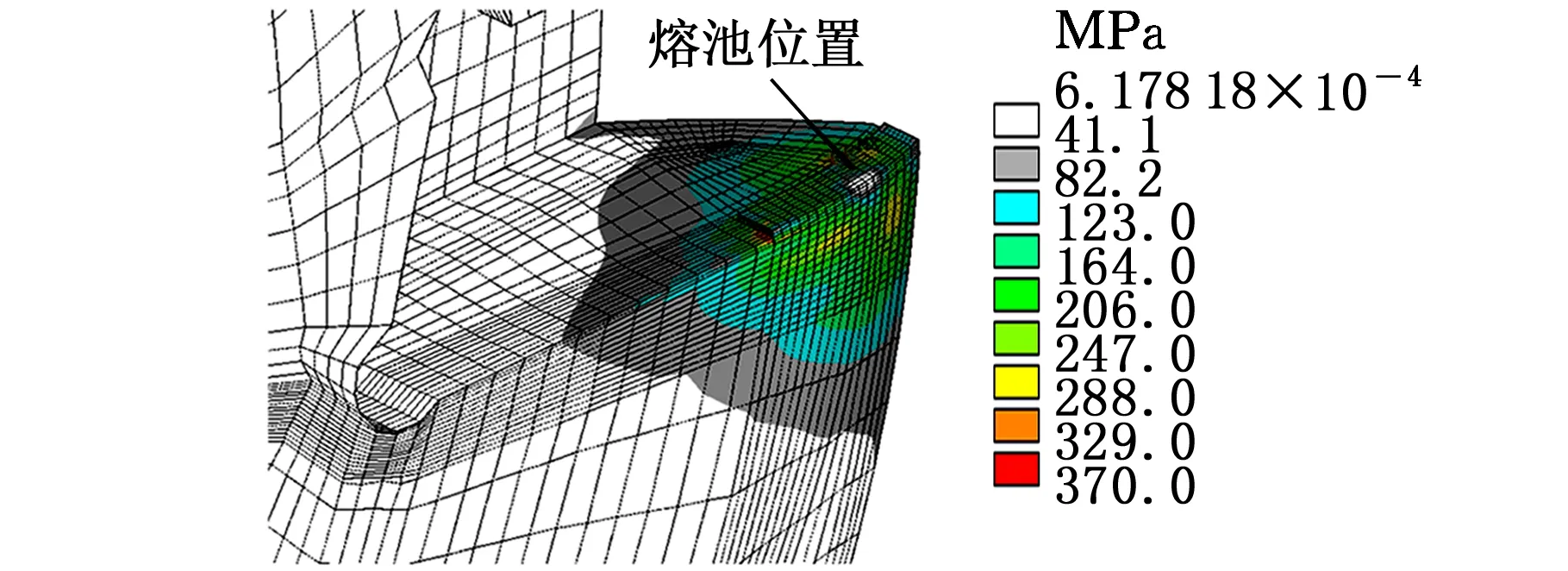
(a)过程应力分布(S=12)

(b)最终等效应力分布(S=114)

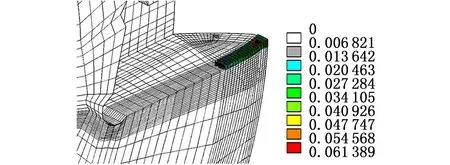
(c)最终等效塑形应变分布(S=114)

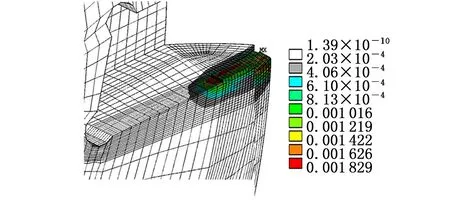
(d)最终等效弹性应变分布(S=114)图8 激光熔覆修复过程的应力及应变云图Fig.8 Distribution of stress and strain of milling cutterdisk in laser cladding repair

综上可知，铣刀盘激光熔覆修复产生的塑性应力集中于结合面的热影响区，这与材料高温屈服产生的塑性应变累积有关。修复后的铣刀盘上残余应力应变具有显著的非均匀分布特征，原因在于非稳态热和几何约束限制的影响。

3 工程应用验证

为了验证有限元仿真结果的正确性以及实际铣刀盘修复部位是否会产生应力开裂的问题，开展工程应用验证实验。铣刀盘损伤部位的切除预处理(台阶高为0.2 mm)采用了DMG铣削中心，激光熔覆修复采用了功率为800 W的YAG激光熔覆成形系统，使用与有限元仿真相同的工艺参数(扫描速度为300 mm/min，光斑直径为2 mm，离焦量为-1 mm，电流为180 A，脉宽为2.8 ms，工作频率为24 Hz，多道搭接的搭接率为40%～50%，送粉速率为21 g/min)，按照预设工艺路径(图2)吹送合金粉末(熔点为1 050 ℃)到工件表面，产生0.4 mm厚的金属熔覆层，修复后再进行加工处理使铣刀盘几何形状和尺寸得以复原，激光熔覆修复后的铣刀盘外观形貌如图9所示。