考虑参数不确定性的转向架构架结构强度分析
2019-02-15智鹏鹏李永华陈秉智
智鹏鹏 李永华 陈秉智
1.大连交通大学机械工程学院,大连,1160282.大连交通大学机车车辆工程学院,大连,116028
0 引言
转向架作为铁道车辆的重要承载部件,是保障行车安全的关键。构架作为转向架的重要零部件之一,不仅起着承载和传力的作用,而且是铁道车辆转向架其他各零部件的安装基础[1]。我国列车运营速度的不断提升以及铁路线路的复杂多变对转向架的结构性能提出了更高的要求。在实际工程设计和分析中所建立的模型都是经过各种假设和理想化而得出的确定性模型。由于加工制造工艺水平的限制和人为因素的存在,使得实际生产的任何产品在材料属性、加工公差和载荷等方面均存在不确定性[2],因此在分析转向架构架的结构强度时考虑参数的不确定性,有助于设计阶段对可能出现的各种问题进行安全评判和设计参数的修改。
目前,已有学者对转向架构架的结构强度进行了研究。李万莉等[3]利用ANSYS Workbench软件根据UIC 615-4-2003标准对新型轨道运料车转向架构架进行了静强度分析。史艳民等[4]对跨座式单轨交通作业车转向架构架进行了基于4种超常载荷工况的静强度和基于Goodman疲劳极限图的疲劳强度分析。李金城等[5]根据欧洲EN 13749标准对70%低地板有轨电车动力转向架构架进行了静强度、疲劳强度和模态分析。周元[6]和卢耀辉等[2]利用ANSYS的PDS模块,对构架静强度可靠性进行分析,得到了转向架构架参数对可靠性的灵敏度。LI等[7]利用改进的正交设计去拟合响应面,并利用ANSYS软件对高速动车组转向架构架焊接接头进行了疲劳可靠性分析,证明了改进正交设计方法的可行性。上述研究多以确定性的参数为属性建立模型,分析转向架构结构强度是否满足标准和要求,未能考虑工程实际中参数的不确定性。基于PDS模块的不确定性分析虽然计算精度高,但是计算效率低,对复杂程度较高或模型较大的结构不适用。
本文以某货车转向架构架为研究对象,综合考虑工程实际中设计参数的不确定性,对转向架构架进行结构强度的可靠性分析,进而评估设计参数的不确定性对转向架构架结构强度的影响。
1 转向架构架设计参数的确定
转向架构架的设计参数对其整体的结构性能有着重要的影响,是设计阶段对结构进行安全评定的基础。为确定关键的设计参数,提高转向架构架结构强度分析的效率,本文根据国际铁路联盟标准UIC 510-3-1994对转向架构架进行结构强度分析。
转向架构架整体采用Shell181壳单元,转臂座采用Solid185实体单元进行网格划分,节点总数为128 819个,单元总数为121 978个。在轴箱吊挂的两个圆孔采用Rbe3单元模拟螺栓连接,同时在两圆孔之间采用Beam188单元模拟螺栓,转臂座之间采用Spring单元COMBIN14模拟弹簧连接,转臂座实体网格与侧梁壳单元采用刚性元模拟连接,单元类型选择CP_STRUC。构架有限元模型见图1。

图1 转向架构架的有限元模型Fig.1 Finite element model of bogie frame
根据UIC 510-3-1994标准规定,转向架构架结构强度的评定为5种超常载荷工况下结构的静强度。本次分析仅施加第一超常工况下的载荷的情况,即在中心盘处施加366 kN的载荷。在一系弹簧单元和转臂座弹簧单元刚性连接处的4个位置分别施加如下约束:Y、Z方向的位移约束,即2和3;Z方向的位移约束,即3;X、Y、Z方向的位移约束,即1、2和3;X、Z方向的位移约束,即1和3。具体约束情况见图2。

图2 转向架构架位移约束Fig.2 The displacement restraint of bogie frame
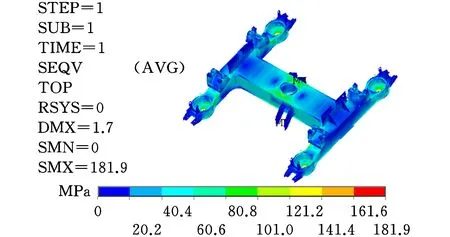
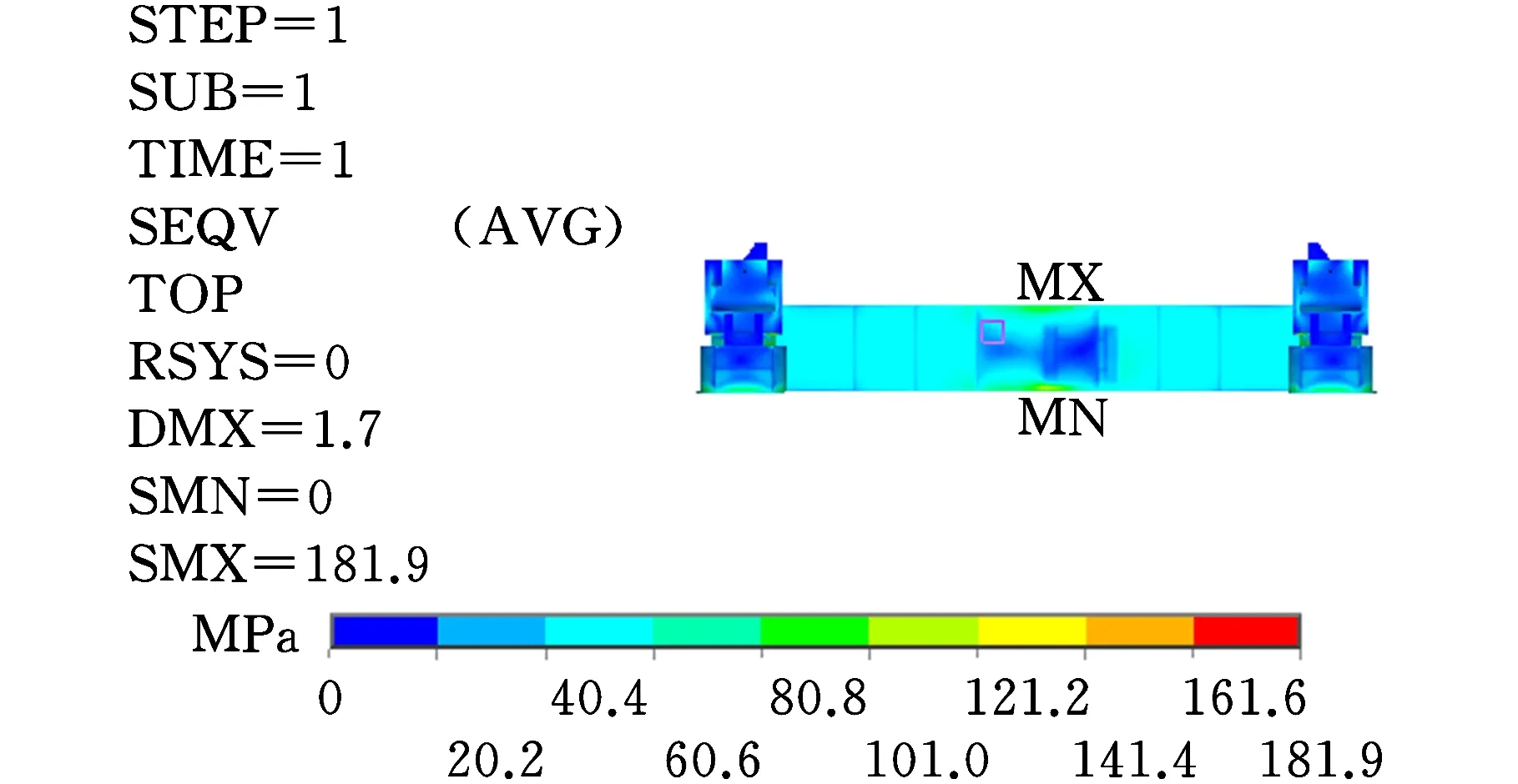
转向架构架钢板材质为Q345E,屈服强度为345 MPa,转向架构架的最大应力取有限元分析结果的最大节点等效应力,构架的应力云图见图3。由图3a可知,转向架构架的最大应力出现在中心销座孔,为181.9 MPa,小于材料的屈服强度。通过分析转向架构架的结构应力可知,构架横梁和侧架的上下盖板与侧板对其结构应力的影响较大,可将其厚度作为结构强度不确定性分析的重要设计参数。
2 不确定性的分析方法
2.1 响应面法
响应面法(response surface methodology,RSM)是一种利用试验设计数据求解多元方程组并进行多元回归分析的经验统计建模技术[8-9]。采用RSM法进行结构强度分析能够较大地提高分析效率,有利于大型复杂模型的不确定性分析。基于响应曲面的转向架构架结构强度分析流程见图4。

(a)正面轴侧图
(b)反面轴侧图
(c)主视图

(d)侧视图图3 转向架构架应力云图Fig.3 The stress nephogram of bogie frame
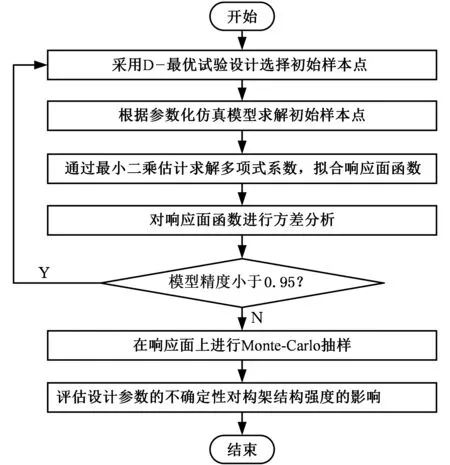
图4 转向架构架结构强度分析流程图Fig.4 The structure strength analysis flow chart of bogie frame
2.2 D-最优试验设计
D-最优试验设计在选择试验运行方面具有较强的预测能力,适用于每一个特定的研究。它可以设计2~24个因素,能够最大限度地减小与该模型系数估计相关的方差,对于高度受限的设计是有用的[10-11]。本文选择该方法对转向架构架进行试验设计。
不论因变量与自变量之间存在何种回归关系,可设其回归模型为
yα=β1f1(xα)+β2f2(xα)+…+βmfm(xα)+εα
(1)
式中,xα为给定的因子区域X中一点,若因子空间为p维欧氏空间,则xα为p维向量,xa=(xα1,xα2,…,xαp);f1(xα),f2(xα),…,fm(xα)为连续函数;β1,β2,…,βm为m个待定系数;εα为服从正态分布的随机变量。
若试验方案由N个试验点x1,x2,…,xN组成,则可以得到式(1)的参数估计:
(2)
信息矩阵
(3)
D-最优设计就是使得信息矩阵的值极大化的一种设计。D-最优试验设计可以使回归系数的估计值b1,b2,…,bp的方差所构成的密集椭球体的体积最小化,同时可以使模型回归预测值方差最大值达到最小[12]。
基于D-最优试验设计提供的初始数据点,采用二次多项式拟合设计参数与响应值的函数关系,并通过最小二乘法估计获得各项的待定系数。为判断拟合的响应面函数能否准确表示转向架构架的结构特征,需要对其进行方差分析(analysis of variance,ANOVA)和精度的检验。表1给出了五因素的方差分析表,其中,n为试验总次数。
通过方差分析能够得到对响应值有显著影响的因素、各因素之间的交互作用以及显著影响因素的水平,进而确定设计参数选择的合理性。
响应面函数精度的测定常采用r检验法。设计参数x的各个观测点与回归方程越靠近,即r2越接近1,表明回归直线和观测点越接近,响应面拟合程度越好,精度越高[13]。

表1 五因素方差分析表
2.3 结构可靠性评估
根据机械结构可靠性评估的应力-强度干涉理论,假定设计参数均服从正态分布,其表达式为
(4)
式中,μX、σX为分布参量,分别表示随机变量X的均值和标准差;x的取值范围为(-∞,∞)。
根据式(4),转向架构架结构可靠性评估的极限状态方程定义如下:
R=fX(x)-S
(5)
式中,fX(x)为构架的最大应力;S为材料屈服强度。
根据式(5),可靠度可定义为
(6)
式中,n′为应力不大于强度(R≤0)的抽样次数;N′为抽样的总次数。
对转向架构架进行可靠性评估,实际是在考虑各设计参数不确定性的条件下,求出R≤0的概率分布特征,评估设计参数的不确定性对结构强度的影响程度。
为提高计算效率,本文采用MCLHS对不确定性设计参数进行随机采样,基本步骤为[14]:①将每个随机变量的分布函数按照等概率原则分成互不重叠的区间;②根据每个随机变量的概率密度函数,从每个区间任意选择一个值;③重复步骤(1)和步骤(2),直到选择了每个随机变量;④将xi的n′个值和xj≠i的n′个值进行随机组合。
3 转向架构架结构强度不确定性分析
3.1 选择初始样本点
根据第1节分析得到的转向架构架的重要设计参数,将板壳厚度和材料的弹性模量作为不确定的设计参数,运用APDL语言对有限元分析模型进行参数化,各设计参数的统计特征见表2。

表2 设计参数统计特征
采用D-最优试验设计选取初始样本点,并将其代入到参数化的有限元分析模型中,得到试验设计后转向架构架的最大应力值。D-最优设计试验及响应值见表3。

表3 D-最优试验设计及响应值
取任意两个设计参数为坐标轴X和Y,根据表3通过MATLAB 2015b编程绘制设计参数的样本空间,见图5。图5能够直观地反映设计点在空间的位置以及重复试验的样本点。由图5可知,31组设计点均匀地分布在样本空间,且某一设计点存在重复设计,其目的在于提升试验结果的可靠度与精确度,减小误差。

(a)设计参数t1、t2对应的样本空间

(b)设计参数t3、t4对应的样本空间图5 设计参数的样本空间Fig.5 Sample space of design parameters
3.2 响应面的建立
根据表3得到的31组包含仿真模型信息的数据点,利用最小二乘法求解多项式的系数,建立转向架构架最大应力的响应曲面函数:
Smax=-3 793.987 84-78.248t1+16.56t2-
176.236 53t3+41.637 2t4+0.053 29E-0.755 89t1t2+
3.487 50t1t3-1.194 47t1t4+1.042 86×10-4E-
2.076 42t2t3+0.794 69t2t4-6.224×10-5t2E-
2.767 99t3t4-8.853 5×10-5t3E-7.016 2×10-5t4E+
1.410 53t12+0.857 15t22+6.920 59t32+0.462 83t42-
1.237 73×10-7E2
(7)
为了更好地观测不确定设计参数和构架结构强度之间的关系,图6和图7分别示出了设计参数对构架结构强度的三维响应曲面图和等高线图。

(a)设计参数t1、t2的响应曲面

(b)设计参数t3、t4的响应曲面图6 设计参数对构架结构强度的响应曲面图Fig.6 Response surface of design parameters forstrength of frame structure
由图6可知,设计参数的变化对转向架构架的结构强度具有一定的影响,由图6a可以看出,侧架侧板和横梁侧板厚度的增加均会导致构架所受应力的减小,与实际情况相符。在相同的厚度变化区间范围内,相比横梁侧板,由侧架侧板厚度变化产生的应力减小程度更大,表明侧架侧板对构架结构强度的敏感性较强。由图6b可以看出,横梁上下盖板对构架结构强度的敏感性较强。设计参数与构架结构强度的等高线形状为椭圆说明两个设计参数的交互作用显著,圆形说明交互作用不显著[15]。由图7可知,设计参数之间的交互作用显著性较低,表明在转向架构架设计时,可以忽略交互作用不显著的设计参数的变化。
3.3 响应面的精度检验
响应面的精度是保证试验设计和响应面函数有效性的基础,是进一步利用该模型进行分析的前提。通过对响应面精度的检验可以获得响应面函数的准确性及选择设计参数的显著性,有助于判定选取的设计参数是否合理。本文利用ANOVA对该模型进行分析,结果见表4。

(a)设计参数t1、t2的等高线
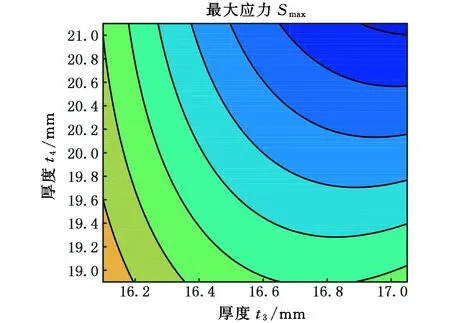
(b)设计参数t3、t4的等高线图7 设计参数对构架结构强度的等高线图Fig.7 Contour diagram of design parameters forstrength of frame structures
表4中,F值和P值均代表相关系数的显著性,F值越大,P值越小,说明相关系数越显著。通过表4可知,该模型的拟合精度较高,且设计参数t1、t2、t3、t4均非常显著,说明设计参数的选择是合理的,能够反映结构强度的变化。参数E表现不显著,说明该设计参数对结构强度影响不大。各设计参数之间的交互作用显著性较低,说明各设计参数的相关性较小,与等高线图的分析结果吻合。响应面函数的测定系数r2为0.994 8,说明拟合程度较高。

表4 响应面函数ANOVA表
为了更好地观测响应面的拟合精度,图8和图9分别给出了试验值和预测值的相关图和残差分布图。由图8和图9可知,所有的设计点均在45°对角线附近,且残差基本控制在2.0范围内,说明转向架构架响应面函数的预测值和试验值相当接近。

图8 试验值和预测值的相关图Fig.8 The correlation between the experimental andpredicted values
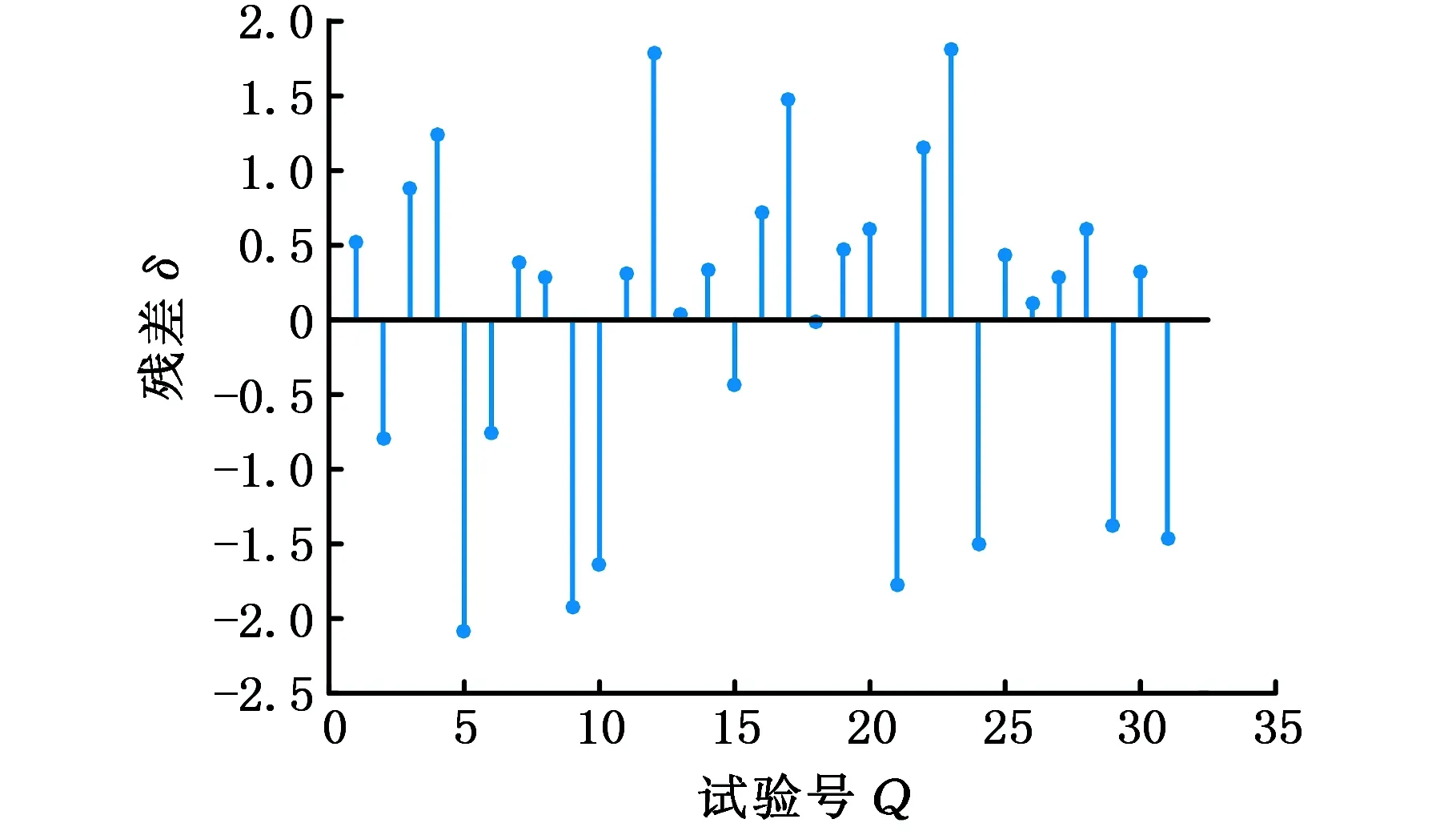
图9 试验值和预测值的残差图Fig.9 The residual values of test and predicted values
3.4 转向架构架结构可靠性评估
基于式(4),利用MATLAB 2015b软件使设计参数均产生10 000个随机数,用以进行可靠性评估,不确定设计参数的概率分布特征见图10。

(a)t1产生的随机分布
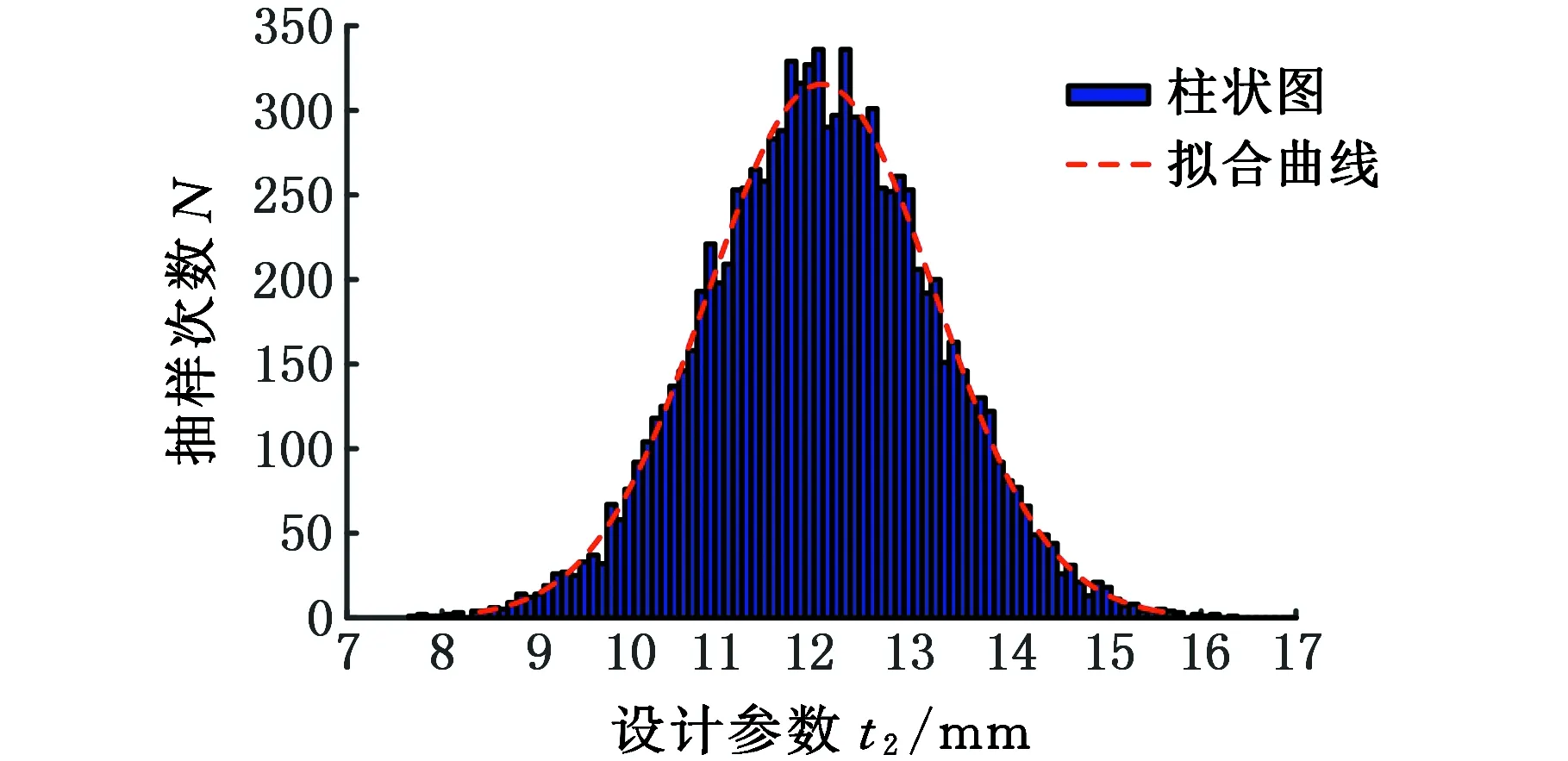
(b)t2产生的随机分布

(c)t3产生的随机分布

(d)t4产生的随机分布图10 不确定设计参数的概率分布特征Fig.10 The probabilistic distribution characteristicsof uncertain design parameters

图11 转向架构架最大应力的频率分布直方图Fig.11 The frequency distribution histogram ofmaximum stress of bogie frame
根据图10所产生的不确定设计参数,运用MCLHS对其进行10 000次抽样,并将结果代入式(7),得到转向架构架最大应力的频率分布直方图,见图11。由图11可知,设计参数的不确定性使转向架构架的结构强度出现了一定的波动,主要分布在150~300 MPa,同时该波动导致转向架构架的最大应力出现超出材料屈服强度的情况。相比传统意义上仅按照标准对构架进行确定性的静强度分析而言,不确定性分析能够更好地评估构架设计的合理性和安全性。
将式(7)得到的计算结果代入式(5),并结合式(6),得到构架结构强度的可靠性评估结果,见图12和图13。

图12 结构强度抽样历史Fig.12 The sampling history of structural strength

图13 结构强度可靠度收敛曲线Fig.13 The convergence curve of structuralstrength reliability
图12展示了进行10 000次计算后转向架构架的强度抽样历史,其中构架应力在200 MPa左右居多。空心圆圈代表应力超过构架材料的屈服强度,说明在这些设计参数范围内构架是不可靠的,安全系数小于1。
由图13可知,当抽样次数较少时,设计参数的随机组合较少,构架所受应力均低于材料的屈服强度,结构可靠度为1。当抽样次数增加,构架的可靠度下降,在500次左右时趋于收敛,得到转向架构架的结构可靠度为0.984 3,相比确定性的结构强度分析,考虑设计参数的不确定性使得计算结果更加贴近工程实际,计算结果更加精确。
4 结论
(1)根据UIC 510-3-1994对转向架构架进行结构强度分析,得到了构架受力较大处的位置为构架横梁、侧架的上下盖板和侧板,并将其厚度确定为结构强度分析的不确定设计参数。
(2)采用D-最优试验设计并结合响应面法,对转向架构架结构强度进行不确定性分析,获得了高精度的响应面,直观地展示了设计参数的变化对构架结构强度的影响和各设计参数之间的交互作用。与传统的直接对设计参数进行抽样的强度计算比较,本文方法提高了分析效率,同时保证了分析结果的准确性,适合其他大型复杂结构的不确定性分析。
(3)基于高精度响应面的结构可靠性评估,进一步验证了考虑不确定设计参数的重要性。转向架构架的结构可靠度为0.984 3,表明了在考虑设计参数不确定的条件下,构架的结构强度有超过材料屈服强度的可能性,即结构失效,因此,为确保结构设计的安全性,在设计过程中考虑参数的不确定性更加符合工程实际的需要。
