考虑硬度的高弹性合金钢3J33微细特征磨削仿真分析及实验研究

2019-02-15徐路遥李蓓智杨建国

中国机械工程 2019年1期

徐路遥李蓓智杨建国

东华大学机械工程学院，上海，201620

0 引言

航天零部件加工具有复杂性，为了节约资源与时间，目前通常采用仿真模拟方式对其加工过程进行研究，在控制挠性接头细筋变形的研究领域中更是如此。陈杰[1]提出通过平衡挠性接头细筋应力的方式控制细筋的加工精度，利用Advant-Edge软件对细筋双侧进行模拟加工，优化了工艺参数。DING 等[2-3]利用有限元分析方法研究了挠性接头细筋在高速磨削时内部的相变变化规律，建立了针对高弹性合金钢3J33考虑相变因素的仿真模型，并得到了相变因素对仿真结果的影响机制。但相关仿真研究几乎不涉及材料硬度的相关描述及其对残余应力的影响。由于挠性接头的细筋尺寸仅为30～40 μm，热处理前后的硬度变化将对挠性接头细筋的残余应力值及其分布状态产生较大影响，从而直接影响仿真分析结果的真实性，进而导致挠性接头的生产合格率。由此可知，考虑材料硬度对微细特征加工残余应力的作用机理是极其重要和必要的。

本文基于有限元仿真方法，针对难以构建多颗磨粒仿真模型的问题，构建了针对挠性接头细筋考虑硬度的单颗磨粒磨削仿真模型，对在不同硬度下磨削时的细筋残余应力分布状态进行了分析对比，并加以实验论证，从而为实际加工生产挠性接头提供一定的理论参考。

1 微细磨削仿真模型的构建

1.1 微细磨削仿真运动几何模型

在挠性接头微孔细筋的微细磨削过程中，磨床的主轴转速极高，最大可达到120 000 r/min，砂轮上的磨粒在细筋微孔上的接触时间很短(时间不长于10 μs)。在这种情况下，可进行微孔的平面化假设，将微孔磨削简化成平面磨削[1，4]。本文在实验和仿真模拟中，采用直径为2 mm、粒度为100目的立方氮化硼(cubic boron nitride, CBN)小砂轮，对微孔直径为2.5 mm的挠性接头细筋进行磨削。将单颗磨粒统一假设成理想锥体，磨粒高度为20 μm，磨粒刃弧半径为5 μm，顶锥半角为53°，则单颗磨粒最大未变形厚度的表达式如下[1，5-6]：

(1)

式中,vw为工件线速度；vs为砂轮线速度；Nd为砂轮动态有效磨刃数；θ为磨粒顶锥半角；ap为磨削深度；ds为砂轮直径；dw为工件直径。

利用有限元仿真模拟软件AdvantEdge中的二维正交微切削模块，构建了图1a所示的单颗磨粒磨削高弹性合金钢3J33的仿真模型。仿真结束后，工件冷却至室温，表面及亚表面的残余应力分布状态见图1b。

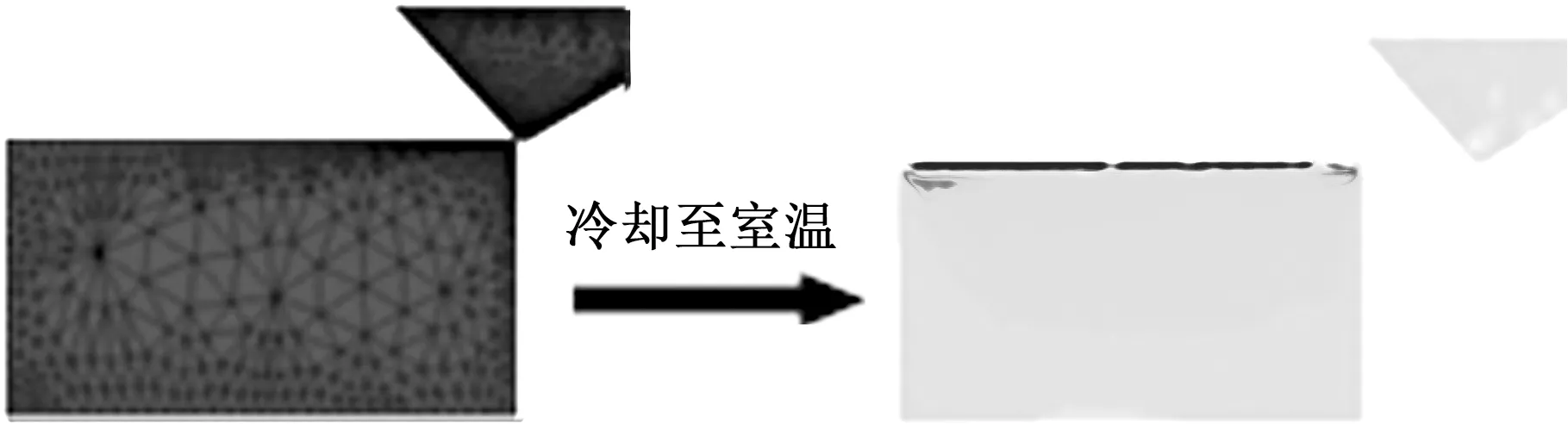
(a)仿真模型 (b)工件残余应力分布图1 残余应力仿真模型Fig.1 Residual stress simulation model

1.2 微细磨削工艺参数设计

在仿真过程中，假设工件转速 (nw=100 r/min) 不变(即工件线速度vw为0.013 1 m/s)，只考虑砂轮线速度vs和最大未变形厚度ag,max的变化，分别选取磨削深度ap为1.5 μm、2.0 μm和3.0 μm。考虑现有纳米磨床主轴的极限转速为120 000 r/min，故在仿真研究过程中选取砂轮转速为90 000 r/min(即砂轮线速度为9.42 m/s)。

1.3 材料本构模型的建立

1.3.1原始模型

细筋的材料选用高弹性合金钢3J33。将砂轮磨粒材料CBN视为刚体，其物理性能参数见表1。

表1 工件与磨粒材料机械物理性能参数

对工件进行微细磨削时，材料会出现应变率强化、应变硬化等变化，因此使用Johnson-Cook模型进行模拟仿真，本构模型的相关参数见表2。模型的计算表达式如下[1,7-8]：

(2)

(3)

表2 3J33的Johnson-Cook模型参数[8]

1.3.2考虑硬度的模型

Johnson-Cook模型中不涉及硬度因素，需增加材料硬度因子及相应的模型，以分析材料硬度对残余应力等表面完整性的作用,因此考虑硬度的方法及其工作流程见图2，其中H表示硬度。表3给出了洛氏硬度在50HRC～52HRC之间的各力学性能参数。

图2 考虑硬度的仿真模型建立流程Fig.2 Establishment process of the simulation modelconsidering hardness

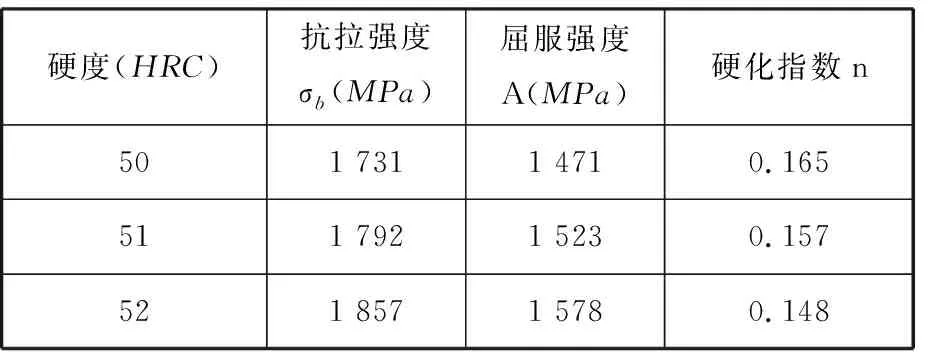
表3 与硬度有关的力学性能参数[9-10]

利用数值分析软件MATLAB对数据进行拟合，分别得到屈服强度A、硬化指数n与硬度H的具体关系表达式：

A(H)=1.4H2-86.9H+2 335.9

(4)

n(H)=-0.004 9H+0.408 6

(5)

将表2中的A值代入式(4)中，得到硬度H为30HRC。工程上用来加工的挠性接头细筋硬度通常在50HRC～55HRC[11]范围内，并用经过热处理后的高弹性合金钢3J33材料进行微细磨削，而目前仿真研究中大多采用未经过热处理、硬度为30HRC左右的材料[12]。研究结果表明[13]，随着材料硬度的提高，切屑从连续带状切屑向锯齿形切屑转变，从而影响切削力、刀具磨损及加工表面质量等，使其体现出不同的特征；且磨削加工与其他加工方式不同，当材料硬度过低时，去除材料时切屑会出现黏性，从而严重影响工件的表面质量，因此构建考虑硬度的仿真模型时，需对细筋工程硬度进行仿真。

1.4 网格划分

在仿真过程中，网格的大小主要取决于最小磨削深度的大小，设最小磨削深度为1.5 μm，则将最小网格细分至0.5 μm。对细筋表层40 μm深度进行细分网格，其最大和最小网格尺寸分别设置为5 μm和 0.5 μm，刀具的最大和最小网格尺寸分别设置为5 μm和 0.5 μm，最终网格划分结果见图3。

图3 刀具、工件网格划分Fig.3 Tool and workpiece meshing

2 细筋微细磨削残余应力对比分析

为了验证考虑硬度模型的正确性，现用考虑硬度的仿真模型分别对硬度为30HRC、40HRC和50HRC的材料进行模拟仿真，得到材料热处理前后对加工工件表面质量的影响规律，并通过实验加以验证。

以砂轮线速度vs=9.42 m/s,磨削深度ap为1.5 μm、2.0 μm和3.0 μm，硬度H为30HRC、40HRC和50HRC的仿真数据为例，图4给出了残余应力分布曲线，其中沿孔径向的残余应力为

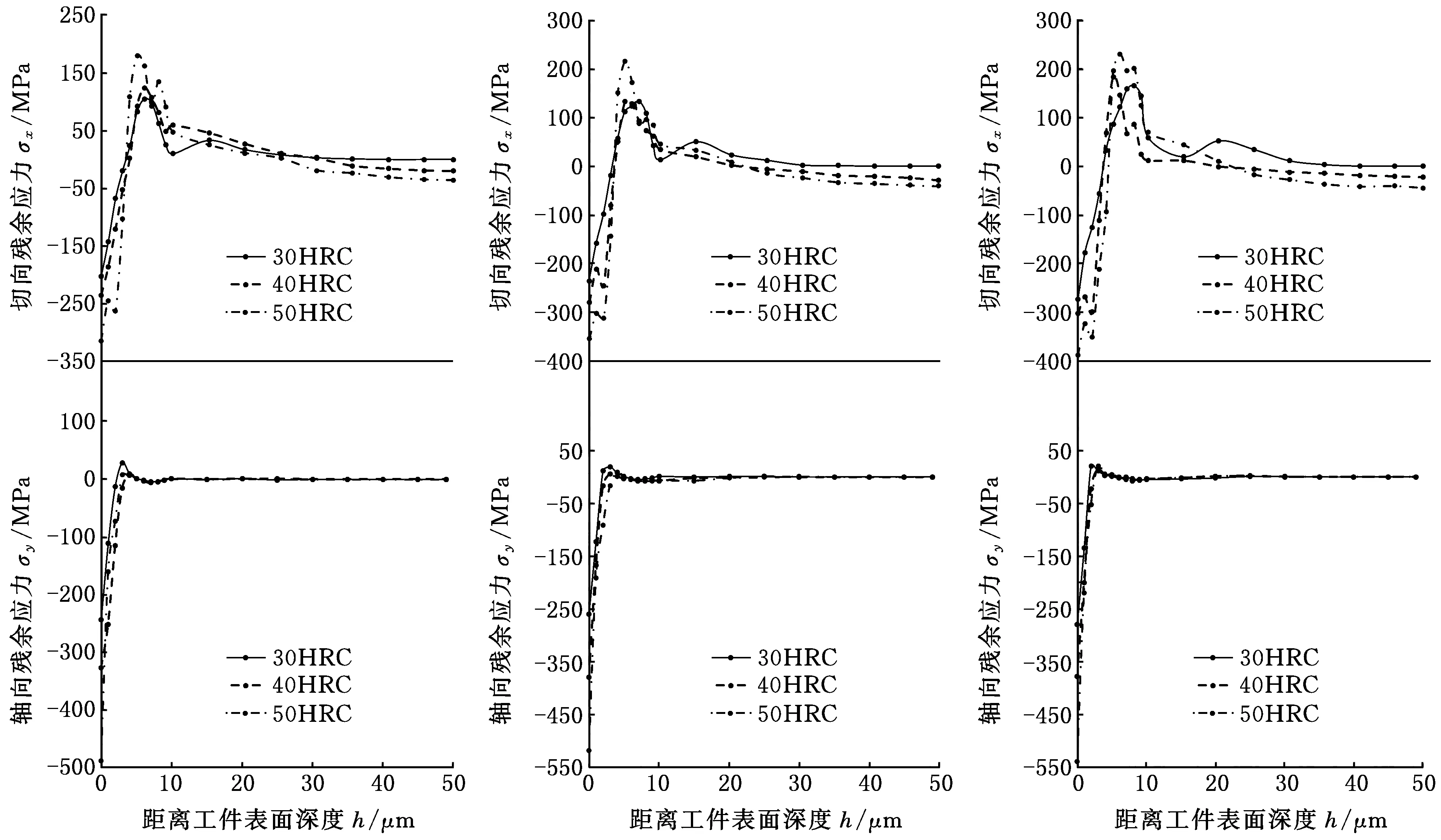
(a)vs=9.42 m/s,ap=1.5 μm (b)vs=9.42 m/s,ap=2.0 μm (c)vs=9.42 m/s,ap=3.0 μm图4 残余应力分布曲线Fig.4 Residual stress distribution curve

切向残余应力，沿轴向的残余应力为轴向残余应力，0 μm处表示工件加工表面，50 μm处表示工件加工面的对侧。

从图4中可以看出，在考虑硬度的仿真模型仿真结果中，当硬度为30HRC时，工件加工面和加工对侧面的残余应力相对于硬度为40HRC和50HRC时的工件加工面和加工对侧面的残余应力小。随着硬度的提高，工件切向和轴向表面(h=0 μm)残余压应力的绝对值均有一定程度的增大，切向亚表面(h>0 μm)的残余拉应力增大，轴向亚表面的残余应力变化不明显，整体切向和轴向残余应力的极差均增大，加工对侧面呈现压应力状态，且这种现象随着磨削深度的增大而更加明显。细筋两侧表面残余压应力的增大，可有效控制其在加工过程中的变形，这种变化也决定了考虑硬度参数仿真模型建立的必要性。

3 实验论证

图5 基础试件与夹具Fig.5 Specimen and fixture

图6 挠性接头细筋微细磨削加工Fig.6 Micro-grinding for flexible joint thin neck

图5所示为基础试件与夹具，试件硬度为50 HRC。图6所示为东华大学和上海机床厂有限公司共同研发的数控纳米曲面磨床，本文在该磨床上进行了挠性接头细筋的磨削实验。仿真验证实验的工艺参数如下：砂轮线速度为9.42 m/s，磨削深度为1.5 μm、2.0 μm和3.0 μm，两轴插补联动速度为0.013 1 m/s。该磨床可用于磨削孔距精度要求很高的精密孔和成形表面，具有精密坐标定位装置。工件装夹在方形定心夹具上，预先在工件圆周面上每隔90°均布钻四组直径约2 mm、深度8 mm的小孔，预留细筋厚度为0.04～0.05 mm。实验采用电镀CBN砂轮(85410-BM)，该砂轮具有工艺简单、制造和使用方便、无需修整等优点，且适合于小孔磨削工艺实验。

为了测试磨削表面残余应力，用PROTO残余应力仪进行测试，借助于X射线测得的细筋表面残余应力对仿真得到的表面残余应力进行校验，如图7所示，残余应力的测试结果见表4。

图7 细筋残余应力测试Fig.7 Residual stress test for thin neck

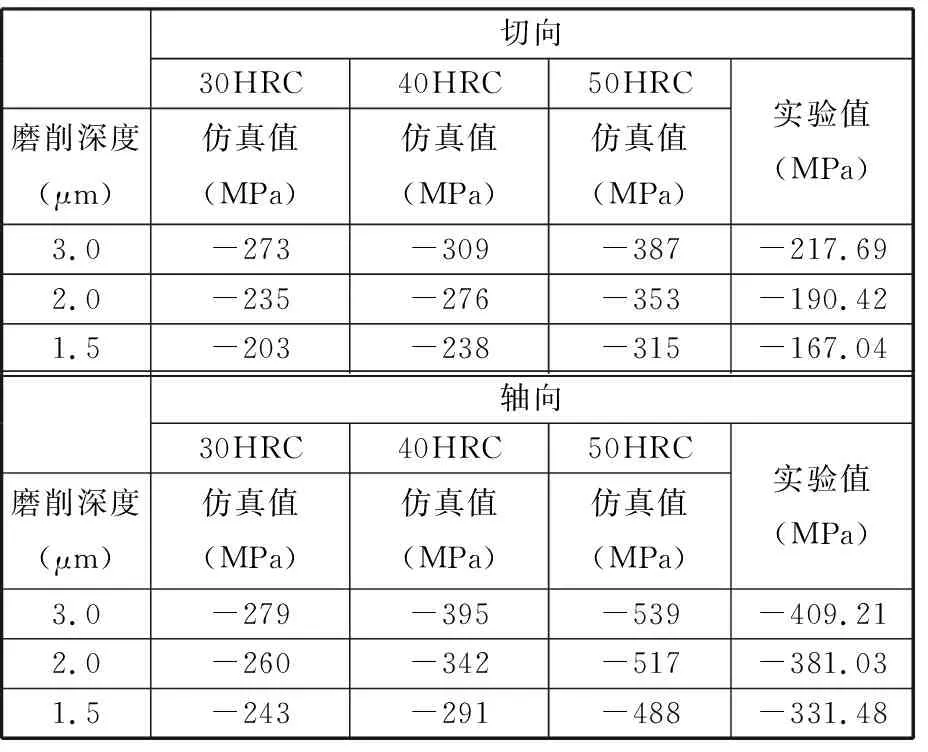
表4 残余应力结果对比

由表4中实验和仿真的对比结果可以看出，在实验过程中，工件切向和轴向表面均呈现残余压应力状态，且轴向残余应力值是切向残余应力值的2倍左右。在仿真过程中，当材料硬度为30HRC和40HRC时，切向和轴向表面的残余应力值相差较小，远达不到2倍的效果，不符合实验所得结论；而与实际应用接近的50HRC材料的仿真结果具有与实验结果相似的特性，基本符合实验所得结论。这种现象主要是因为在挠性接头细筋磨削的过程中，硬度为30HRC的材料进行磨削时会出现黏性，工件表面呈现较小的残余压应力，该现象并非工程所需。在未建立考虑硬度的模型前，通常将硬度为30HRC材料的仿真参数仿真得到的结果与实际硬度为50HRC材料的实验结果进行对比，结果易出现较大出入，从而失去了仿真的意义。而通过对仿真模型进行优化，加入考虑硬度参数后，使仿真可以根据工件的实际硬度进行仿真，由此得到的仿真结果与实验结果的趋势一致，可以认为考虑硬度的仿真模型具有有效性及可靠性。