产品族架构设计与供应商选择的主从关联优化
2019-02-15关进良熊奕璇马玉洁
杜 纲 关进良 熊奕璇 马玉洁
天津大学管理与经济学部,天津,300072
0 引言
随着市场多样化和个性化需求的发展,企业面临着巨大的挑战,需要在控制成本的前提下迎合不同市场中的顾客需求,因此,产品族已经成为企业产品开发的基本单元[1]。供应商是构成企业竞争力的一个必不可少的要素,供应商的选择也直接影响着供应链的整体性、连续性和协调性。供应商的供货能力、所提供的物料质量等直接影响所制造产品的质量,以及企业的效益,从而对企业竞争力造成影响[2]。目前有关产品族设计与供应商选择的研究较多,且理论体系逐渐成熟,但大部分有关产品族设计与供应商选择的文献都是定性分析,相关的定量分析文章相对较少,且大部分研究只考虑单一环境中产品族设计与供应商选择的优化[3-5],极少将两者联合考虑进行优化。客车底盘是具有模块化特性的产品,牛连防[6]从技术、经济和社会3个指标方面构建了底盘产品族的评价指标体系,并认为底盘产品族的模块选择与供应商有很大联系。DU等[7]采用通用产品结构来描述产品族中具有层次结构的模块组织、模块实例与产品变形,并开发不同的变异或衍生产品来满足不同的市场需求。ZHANG等[8]考虑模块选择和供应商的选择,建立整合平台产品设计和物料购买决策的混合线性规划模型。LUO等[9]对模块选择和供应商选择进行研究,建立了单层优化模型。CAO等[10]针对供应商设计阶段进行研究,探讨基于平台的产品供应商预选择,最小化外包成本和供应商风险。
上述优化方案忽略了两种不同决策问题之间的协调,只是简单地将产品问题与供应商选择问题进行线性结合,实际上产品族配置与供应商选择在决策主体、目标等方面是一个主从关联的协调设计与优化问题,两者在研究过程中并不是彼此独立的,而是相互影响和关联的。供应商的选择一般要服从产品族的整体利益,而产品族中的架构设计对下层供应商的相关因素具有影响和约束,进而影响整个供应商的选择[11]。
目前,许多学者研究了供应商评价的多种准则。马士华等[12]在参阅国外相关研究文献的基础上,提出企业业绩、生产能力、质量和企业环境等四项一级指标的供应链合作伙伴评价体系。为了使风险降到最低,朱兵[13]结合质量系统、环境、绩效等指标建立评价系统对供应商进行选择。侯萍[14]对电商企业的电子采购过程进行了研究,确定由质量、绩效、服务、环境等指标构成的供应商评价体系。刘晓等[15]采用分类的方法,深入分析推式采购和拉式采购环境下的供应商选择模型与方法。上述研究都只考虑供应链中的因素来确定供应商选择指标,并未结合产品族设计来考虑供应商选择。
双层规划是指模型的约束中包含子优化问题的数学规划[16],双层规划虽然可以作为数学规划的一种推广形式,但它与普通数学规划有着很大的不同,由于其模型的上层中含有下层的最优解或最优值函数,使得模型成为一个非光滑的优化问题,并且当上层的约束中含有下层的最优解时其可行域可能是不连通的。目前双层规划被应用在不同的领域,但将双层优化的模型与方法应用于产品族优化设计的研究仍较少。
本文在已有研究的基础上,将产品族模块架构设计和供应商的选择分别作为主、从规划问题,构建了一个双层规划模型并提出了包括优化模型、计算求解等在内的一整套关联优化方法,并将该方法应用于某汽车底盘产品族架构设计及供应商选择的案例中。
1 问题描述
本文将产品族架构设计与供应商选择进行协同优化,最大化制造商的利益。产品族架构设计与供应商选择问题就是产品空间决策问题与供应链空间决策问题。由于产品族架构设计是产品族设计的前端环节,在时间顺序及层次上位于供应商选择的前一层次,并且产品族架构设计的结果将作为供应商选择的输入,供应商选择的结果又是对产品族架构设计的评价,故两者是一个具有主从关系的关联优化问题,其中产品族架构为主,供应商选择为从。产品由通用模块和可选模块组成,每个可选模块都有各自的模块候选项,每个模块候选项对应不同的供应商。根据模块功能和效用的不同,由多个基本模块组成的模块为复合模块。供应商选择方案为从供应商集合中选择合适的供应商来供应产品族的可选模块,见图1。

图1 问题图Fig.1 Problem diagram
在此协同优化问题中,已知产品族的所有基本模块集合{1,2,…,k,…,K}和对应的模块备选项集合{1,2,…,lk,…,Lk},以及这些模块备选项的功能效用uikl。基本模块分为通用模块和可选模块,通用模块是构成产品族产品平台的必要元素,可选模块是形成产品族差异化的元素。通用模块集合和可选模块集合的信息已知。优化模型模块的一般形式记为mk,k∈{1,2,…,K},每种模块mk有lk个候选项,则第k种模块的第l个候选项表示为mkl。产品族架构设计问题也可以描述为在所有模块组合中进行选择,组合成不同的产品变形问题。产品变形的集合为P(P={Pj,j=1,2,…,J})。针对供应商选择问题,已知供应商的集合{1,2,…,s,…,S},以及制造商将零件交给供应商进行生产的固定投资、模块的采购成本及风险成本。根据产品的模块选择决策来判断哪些模块由哪些供应商提供。
1.1 变量与参数
基于以上对问题的分析和决策机制,根据Stackelberg理论构建双层主从关联优化模型,并对模型的上层和下层构建及模型的主从关联进行分析和研究[17]。其中产品架构设计扮演领导者的角色,供应商的选择扮演跟随者的角色。本文所涉及的参数如下。
(1)集合包括市场的种类I、产品的种类J、基本模块的种类K、模块备选项的种类L、供应商的种类S。
(2)决策变量包括xjrkl、ykls。xjrkl表示第j个产品变形的第r个复合模块是否选择第k个基本模块的第l个模块备选项,ykls表示供应商s提供模块k的备选项l。

产品族架构的目标是极大化效用与成本比值,决策产品族的模块选择。记X={X1,…,Xj,…,XJ}={…,xjr,…,xjR,…}={…,xjr1,…,xjrK,…}={…,xjrk1,…,xjrkL,…},上层决策变量为xjrkl。下层供应商选择受上层产品族架构方案的约束,需要决策由哪个供应商来提供可选模块。图2所示为主从规划模型的决策变量结构。上层根据已知信息选择模块,对产品族架构设计进行优化,下层根据上层传递下来的变量xjrkl选择相应的供应商,对总成本进行优化,并将优化结果ykls反馈给上层。
1.2 上层
模型的上层是对产品族架构进行优化,求产品族设计方案。上层的目标函数是表示配置决策的依据,也是对配置决策的一种评价。评价最基本的准则是客户利益和企业利益的极大化,这是由企业发展产品族的根本目的所决定的[18]。本文将单位成本效用作为产品族配置的优化目标。客户利益是指客户认为产品对自己核心需求的贡献和满足程度,本文采用客户认为的产品效用Uij来表示。为便于度量,将Uij分解为如下来自客户认为各模块的综合效用:
(1)
式中,wjk为第k个模块在产品变形Pj中的权重。
上层模型表达为
(2)
(3)
xjrkl≥xjrklRkk′
(4)
r∈{1,2,…,R};k,k′∈{1,2,…,K}
(5)
(6)
(7)
R∈N+xjrkl∈{0,1}
(8)
式中,C为总成本;Rkk′为制造基本模块k和基本模块k′的耦合系数。
顾客选择产品受到自身、外界环境等各种因素的影响,式(3)表示细分市场i中产品j被顾客选择的概率,可由客户效用的概率选择规则(MNL)方法计算得到。产品族架构设计约束根据工程经济学和逻辑性约束来建立,如产品族中模块制造、组装的关联约束。式(4)表示有关联的模块必须组装到同一复合模块中。式(5)表示产品差异性,确保不同的产品有不同的模块组成方式。式(6)确保每个产品复合模块中的基本模块的模块备选项不重复。式(7)表示每个基本模块只能选择一个备选项或者不被选择。式(8)表示决策变量的逻辑约束。
1.3 下层
模型上层决策产品族架构,决定每个产品变形的模块配置选择xjrkl,并将xjrkl传递给下层。下层的目标函数是供应商的总成本,总成本包括固定成本、供应商采购成本和风险成本。下层将决策结果反馈给上层,根据最终成本来影响上层产品族架构设计决策,总成本C是极小化目标,即
minC(xjrkl,ykls)=CF+CM+CR
(9)
(10)
(11)
式中,CF为固定成本;CM为供应商的供货成本;CR为供应商的风险成本。
下层约束主要为逻辑约束:
(12)
ykls∈{0,1}
(13)
式中,Njks为每个供应商s提供模块k的备选项l的量;Ns为供应商的供货能力。
式(12)为供应商供货能力约束,每个供应商s提供模块k的备选项l的量的总和不超过自身的供货能力。式(13)表示决策变量在0和1之间取值。
1.4 整合优化模型
基于上下层模型,可以建立产品族架构设计与供应商选择关联优化的双层规划模型:
(14)
minC(X,Y)=CF+CM+CR
(15)
其中上下层各自一些兼容性约束将在案例分析中根据实际情况给出。式(14)的约束条件为式(4)~式(8),式(15)的约束条件为式(12)、式(13)。
产品族架构设计和供应商选择的联合优化问题可作为一个主从优化模型进行建模,产品族架构设计优化为主,供应商选择为从。产品族架构设计是对变形产品选择、模块选择和基本备选项选择进行决策,也就是确定决策变量xjrkl。供应商决策就是将产品Pj的成本反馈给上层,即下层将最优成本C反馈给上层,影响上层的综合效用。模型经计算得到最优解(X*,Y*),即最优产品族架构方案和供应商选择方案。
2 模型求解
2.1 算法构建
双层模型求解方法可分为直接方法和间接方法两类。直接方法是依据双层规划的决策机制直接求解,首先由上层模型的优化目标求出一个解,同时下层以该解中的上层变量为参变量求解下层模型,采用某种优化规则进行迭代,直至得到最优解。间接方法是在一定条件下将模型先转化为等价的单层问题,然后通过求解单层问题得到双层规划的解。转化为单层的主要方法是当下层每个模型都是一个凸规划时,将下层问题由其KKT条件代替。由于模型是一个规模较大的0-1非线性规划问题,为使所构建的遗传算法具有全局收敛性,本文构建了双层嵌套遗传算法,利用外层遗传算法求解上层问题,将上层问题的决策变量X*传递给下层,内层遗传算法以此为参数进行求解,然后将求解出的下层问题最优结果Y*返回给上层进行迭代。
2.2 求解过程
2.2.1变量处理
为缩小搜索空间和保持染色体中片段对约束的满足优势,需对算法编码和算子进行设置。
(1)编码选择。遗传算法的实现基础是将待解决的问题表示为一个有限长度的串,称为染色体。基于双层决策模型,本文采用嵌套式遗传算法,编码分为上层(ULC)与下层(LLC)两部分,且上下层染色体都对应于各自的解X和Y。图3给出了上层问题的染色体编码,上层问题染色体的长度就是模块备选项的总数,为J×R×K×L,染色体中的每个基因代表一个模块备选项。根据上层的结果,每条染色体对应一个基本模块,每个基因代表基本模块所对应的模块备选项的选择。下层问题染色体长度为K×L×S,每个基因表示对应每个产品的供应商,具体编码见图4。
(2)交叉与变异。染色体间要在一定的约束下完成交叉与变异。遗传算法中的交叉是指任意选择两个父代染色体以一定的概率交换他们其中的一部分基因。当一对染色体被选择后,他们各自将会随机产生两个交叉点,同时交换的范围也被确定,通过交换选择的染色体的片段得到子代染色体。变异出现在交叉之后,并作用于独立的后代,它以小概率随机挑选一个基因,并且改变其模块实例。

图3 上层变量编码示例Fig.3 Example of upper-level variable encoding

图4 下层变量编码示例Fig.4 Example of lower-level variable encoding
2.2.2求解流程
产品族架构设计优化与供应商选择问题主从关联优化模型是一个0-1非线性双层整数规划模型。基于上节分析,本文构建了一个嵌套遗传算法用于解决这类双层规划问题,具体求解流程见图5。

图5 遗传算法流程图Fig.5 Genetic algorithm flow chart
(1)确定产品数J和复合模块数R,并初始化种群。根据上层变量规模随机生成种群规模N,且满足边界约束。
(2)判断种群是否满足上层约束,若满足,则代入下层,若不满足,则将适应度设为零,转下一步。
(3)上层判断种群是否达到最大代数,若已达到最大代数,则记录最优值,转入下一步,若未达到最大代数,则进入排序、选择、交叉与变异过程,之后再进入步骤(2),重复。
(4)下层将上层可行个体代入并初始化生成下层种群Y,下层验证种群可行性,若满足则进行适应度评价,若不满足则将适应度设为零。
(5)判断下层种群是否达到最大代数,若达到则记录下层最优个体与最优值,若未达到则返回步骤(4)并重复至最大代数。
(6)将下层最优个体与最优值代入上层计算效用比成本值,并进行适应度值评价。
(7)判断种群是否达到最大代数,达到则记录最优解与最优值,未达到则重复步骤(3)直至最大代数。
(8)记录上层最优解与最优值后判断模块数是否取完所有可行值,若取完则结束,若没取完则返回步骤(1),重复。
3 案例研究
3.1 背景介绍
以某品牌客车为例介绍本文优化模型的应用求解。根据实际调研及资料查阅,选取了底盘的主要部件,忽略部分部件,如变速箱和传动轴。将客车的底盘分为发动机、传动系统、行驶系统、转向系统和制动系统五部分,这五个部分又分为机体组、供给系统等细分模块,并将这些基本模块分为通用模块和可选模块。客车底盘模块结构见图6。
基本模块的效用和成本等信息见表1。本文只考虑一个主要的目标市场,也就是I=1,市场规模Q=20 000。供应商s提供模块k的备选项l发生风险的概率rkls通过给出的供应商在不同可选模块中各模块候选项的供货可靠性值来确定。

图6 客车底盘模块结构图Fig.6 Bus chassis module structure
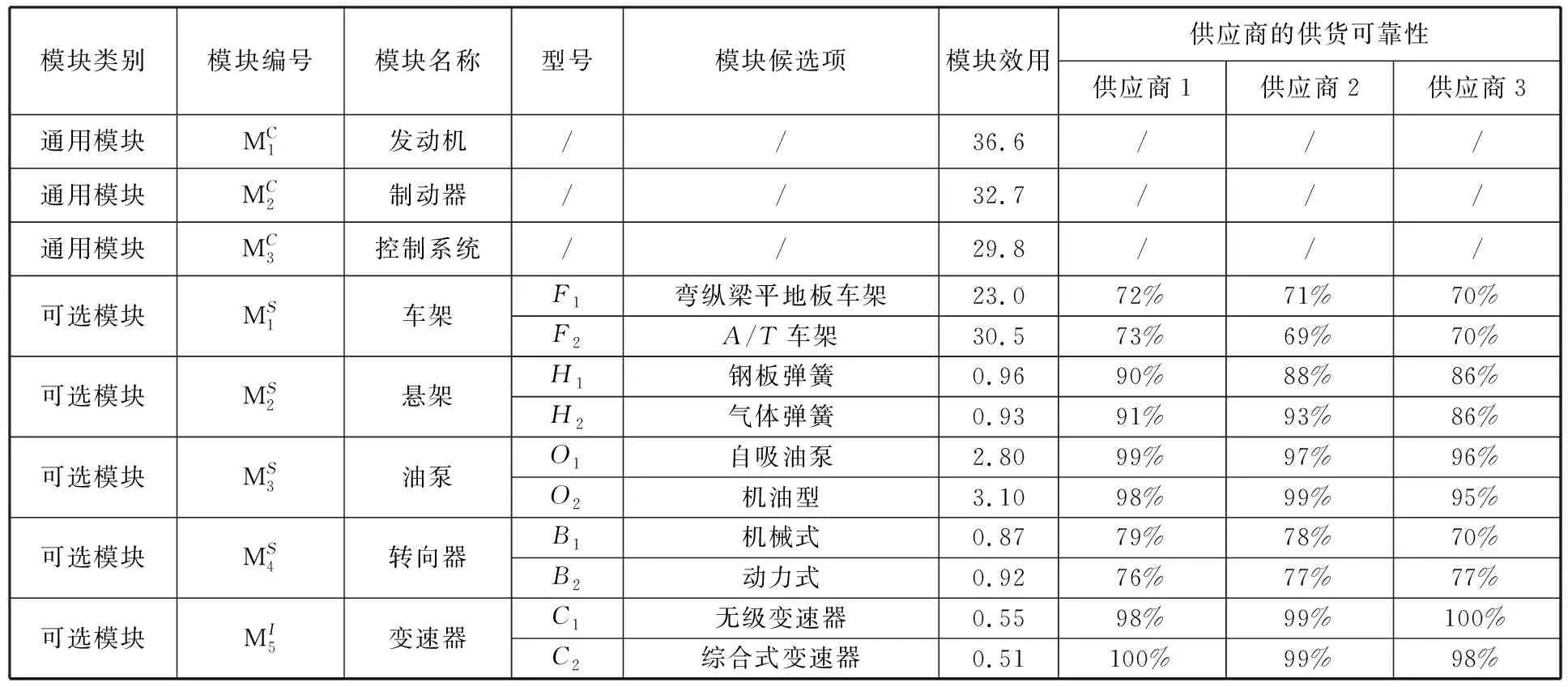
表1 客车模块分类及效用
注: “/”表示不考虑型号,没有模块候选项和供应商
根据企业调研和实际生产情况,本案例中客车底盘产品族的供应商采购成本和组装成本等已知信息见表2。总成本为不同模块在选择不同供应商时,供应商采购成本和风险成本的综合。

表2 供应商采购成本和组装成本
3.2 计算求解
由于本文研究的模型为双层规划模型,解析方法很难准确求解,而智能遗传算法较为适用于非线性规划且含有0-1变量的问题,因此本文采用遗传算法对含有0-1变量的双层规划模型进行求解,利用MATLAB工具箱中的遗传算法功能实现。为了进一步优化,本文分别对产品数J取值为2、3,复合模块数R取值为2、3,即求解4次,比较得到最优值。设定初始种群规模为100,交叉概率为0.8,变异概率为0.01,迭代次数为200。计算结果趋势图见图7。由于纵坐标是产品类别和复合模块不同情况下的函数值,且把4组迭代次数为200的函数值放在同一个图表中,故纵坐标跨度较大,这导致函数收敛结果从直观来看收敛速度较快,其实则不然,每种情况都需要经过较多次迭代才趋于稳定,所得解满足双层规划约束域且算法全局收敛。

图7 趋势收敛图Fig.7 Trend convergence graph
传统结合供应商设计的产品族配置过程中使用的优化方法主要有两阶段单层优化(non-joint optimization,NJOP)和集成单层优化(all-in-one,AIO)方法。两阶段单层优化中第一阶段以效用最大为目标,进行产品族架构设计优化;第二阶段以成本最小为目标,进行供应商选择设计。这种方法把一个问题割裂为两个问题来进行优化,与双层优化相比,不具有完整性。集成单层优化通过建立单目标优化模型来同时进行产品族架构与供应商设计,其目标是最大化的效用与成本。集成优化方法把两个主体的优化问题合二为一,不能准确表示模型。
3.3 结果分析
由图7及表3可以看出,在J=3,R=3的情况下,取得最优值。当J=3,R=3时,上下层目标相互关联优化。表3给出了最优情况下的具体结果,在J=3,R=3的情况下,产品族架构设计最优的效用与成本的比值为0.000 598 66,总成本为554 000 000元。最优方案的产品族架构设计方案和供应商选择方案具体分析如表4和表5所示。
3.4 灵敏度分析
采用遗传算法研究参数μ对上层和下层目标函数最优值的影响,即敏感度分析。μ的取值从0.1到2.1,每次增加0.2,观察上下层目标函数的变化范围,见图8。从图8中可以观察到,μ的取值范围为0.1~1.3时,下层优化的目标函数值不变,为554 000 000元;在1.3到2.1之间,随着μ的变化,下层目标函数值不断波动。μ取值在0.1到1.7之间时,上层目标函数值基本保持不变;μ取值在1.7到2.1之间时,上层目标函数值随着μ的不断增大而增大。

表3 最终方案

表4 产品族模块选择方案

表5 供应商选择方案
注:“”表示该模块由相对应的供应商进行提供

图8 μ变化影响图Fig.8 μ change impacts graph
由实验可知,μ不仅可以影响上层目标函值,在一定情况下,也同样影响下层目标函数值,因此,在客户购买行为建模初期,公司应该对μ的正确校准给予足够的重视。
4 结论
本文对产品族架构设计与供应商选择问题进行研究,建立了产品族架构设计与供应商选择问题协同优化的主从关联优化模型,并应用于客车底盘产品族案例。通过分析计算认为,产品族架构设计与供应商选择问题是相互关联且具有主从关系的,基于主从关联结构建立模型,不仅可从工程视角展现产品族架构设计,也体现了供应商选择问题对产品族架构设计的反馈与要求。本文采用双层嵌套遗传算法及相关处理策略更符合关联优化模型的特点,所得解满足双层规划约束域且算法全局收敛。本文将产品族架构设计与供应商的设计进行关联优化,不仅能够使产品的总成本达到最小,也保障了客户的效用最大化。本研究能够帮助企业的决策者更好地对产品进行设计,为企业增加利润的同时,有效提高企业的竞争力。另外,本文所给出的客车底盘产品族的应用案例表明主从关联优化方法可得到更加合理的结果。
