莱斯校正的NLM算法在扩散加权图像中的应用

易三莉,李思洁,贺建峰,张桂芳

(昆明理工大学 信息工程与自动化学院,昆明 650500)

1 引 言

扩散张量成像(Diffusion Tensor Imaging,DTI)技术是目前唯一非侵入活体获取脑白质结构的技术,该成像技术通过检测水分子在大脑中的扩散情况来获取其各向异性等信息.从扩散张量图像中能够较早发现急性脑梗塞症状,能够揭示脑瘤如何影响神经细胞连接等大脑问题,因此扩散张量图像在医学上具有很重要的意义.

DTI数据是由扩散加权图像(Diffusion-Weighted Image,DWI)计算得到,DWI图像在获取和传输的过程中,均要受到一定程度的噪声污染.噪声会对获取的DTI数据产生较大的偏差,从而影响其后续的相关研究.因此在计算DTI数据之前对DWI图像进行降噪是十分重要的.

目前国内外对DWI图像进行降噪的技术有很多,Bao等人通过定义了一个基于局部均值和改进的相似度量,提出将结构自适应稀疏的方法应用于DWI图像降噪,该算法能够较好的减少DWI图像中的噪声[1].Liu M等人提出一种用于同时平滑和估计DTI图像的鲁棒变分法,该算法直接对DTI降噪,实现有效降噪的同时减少了计算时间,但是该算法不是直接处理DWI图像中的噪声,因而DTI数据存在可靠性问题[2].张瑞等人提出的全局稀疏梯度耦合张量扩散的图像去噪模型[3].Haldar J P等人利用数据集中所观察到的高水平结构相似性,采用统计重构的方法,在提高信噪比的同时保持了DWI图像的分辨率[4].Zhang等人提出的使用高阶奇异值分解对DWI进行降噪,显著减少了在处理图像的过程中产生的伪条纹[5].Lam等人将降噪问题看成一个包含边缘和低秩模型的最大后验估计问题,通过秩和边缘的约束有效提高了DWI图像的信噪比,从而提高扩散参数估计精度且提高了执行效率[6-8].McGraw T等人提出通过加权全变分(Total Variation,TV)范数最小化对扩散加权图像数据进行平滑,该算法较好的实现了对DWI图像的平滑[9].张相芬提出的基于各向异性扩散的DTI图像恢复,主要采用的是经典的各向异性(Perona-Malik,PM)算法,能够较好的保存图像的边缘[10].国内也有许多学者主要以神经纤维跟踪的研究为主,但在处理图像时提出了对DWI图像的滤波算法[11,12].以上算法均能够有效的改善DWI图像的质量,但是这些算法都没关注到DWI图像中的纹理细节信息.

DWI图像具有两个特点:一个是图像的自相似性程度高,纹理和结构具有重复出现的特性并且纹理细节较多;另一个是图像中所含噪声为莱斯噪声.非局部均值滤波算法能够利用图像自相似性的特点,通过图像块的方式在整幅图像范围内查找相似像素,并根据相似像素得到降噪后的像素值.由于它采用了整幅图像中的相似像素来对目标像素进行计算,因此该算法能够更好地保留图像中的纹理细节.但该算法通常用于图像噪声为高斯分布的情况,对于噪声分布为莱斯分布的DWI图像,算法的降噪效果将受到一定的影响.基于上述特点,本文提出一种将莱斯校正与非局部均值滤波算法相结合的改进算法,使得非局部均值滤波算法更好地应用到DWI图像的降噪中,从而实现在对DWI图像进行降噪的同时能够更好地保存图像中的纹理细节.

2 扩散张量成像

人体大脑中水分子的扩散运动可以通过扩散张量来表示,其扩散状态可以间接的反映组织微观结构特点及其变化.扩散张量由一个3×3的对称正定矩阵组成,一般用D表示如下:

(1)

(2)

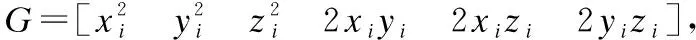
根据公式(2)可知DTI图像的计算源于基准图像S0和加权的核磁图像Si,而这些图像在获取过程中均会受到噪声污染,且由于Si是施加了扩散敏感梯度的DWI图像因此所含噪声更多图像更模糊,从而使计算得到的DTI数据不可靠.并且由于公式(2)是关于方程组的计算,这个方程组对噪声十分敏感[15],即使微小的偏差也会对扩散张量数据产生较大的影响.因此,对DWI进行降噪对DTI的计算及其后续研究都具有非常重要的意义.

3 莱斯校正的非局部均值滤波算法

图像中普遍存在自相似性,即图像的纹理和结构具有重复出现的特性,人的大脑图像在这一方面尤为突出.这种特性体现在图像中即为数据具有冗余性,图像数据本身存在相关性,这在图像处理上具有较大的意义.DWI图像同样具有自相似性程度高,含有较多纹理细节的特点且图像中所含噪声为莱斯噪声.由于非局部均值滤波器能够利用图像的自相似性对图像进行降噪,因而能够更有效地保留图像的细节纹理等信息.但该算法通常用于处理噪声分布为高斯分布的图像,对于噪声分布为莱斯分布的DWI图像则需要进行莱斯校正.

因此本文提出一种将莱斯校正和非局部均值滤波相结合的算法,称为莱斯校正的非局部均值滤波算法(Rician Correction Non-Local Means,RCNLM).该算法能够更好的实现对DWI图像的降噪.算法分为两个部分,首先对DWI图像进行莱斯校正,然后采用非局部均值滤波器对莱斯校正后的DWI图像进行降噪.

3.1 莱斯校正

DWI图像中每个像素的信号都是由实部与虚部所组成的复数信号,因此DWI图像中含有实部和虚部两个部分的高斯噪声.此时图像中的噪声已经不是简单的高斯噪声了,而是莱斯噪声.莱斯噪声与信号是相关的,受到莱斯噪声干扰的DWI信号为莱斯分布,它的分布函数如下[16]:

(3)

(4)

而公式(4)是瑞利分布的概率密度函数[18,19].表示当K→0时,莱斯分布趋向于瑞利分布.当K→时,y≈s,此时公式(3)变为:

(5)

而公式(5)为高斯分布函数.从以上的公式推导可知:当莱斯因子K的值趋向于0时,它的分布趋向于瑞利分布;而当莱斯因子K的值无穷大时,莱斯分布近似于高斯分布,实际上当K≫1时,莱斯分布就趋向于高斯分布了.

通过上述结论可以看出,在一幅图像中若莱斯因子的值趋向于0,则图像中所含噪声分布为瑞利分布;而若莱斯因子的值较大时,图像中所含噪声分布为高斯分布.因此,根据莱斯噪声的特点先对图像进行莱斯校正.由于莱斯因子和信噪比是相关的,所以莱斯校正通过利用图像的信噪比和阈值进行比较,将图像中的像素进行分类.当图像的信噪比高于阈值时,认为图像中所含噪声为高斯噪声,则使用非局部均值滤波算法对该点进行降噪;当图像信噪比低于阈值时,认为其所含噪声为其他噪声,则将该像素点置零.具体公式如下:

(6)

其中,u为观察图像,i为目标像素,S是以目标像素i为中心的图像块的信噪比,t为阈值.在进行莱斯校正处理时,我们通过用图像块的方式来计算目标像素的信噪比,将信噪比与阈值进行比较后对目标像素进行分类,对不同类别的像素使用不同的方法进行处理.文献[20]中证明了当图像的信噪比S大于1.913时,可以认为图像所含噪声分布为高斯分布,也就认为此时图像中所含噪声为高斯噪声.

经过莱斯校正处理后的DWI图像符合图像噪声高斯分布的特点,此时可采用非局部均值滤波器对校正后的DWI图像进行降噪.

3.2 非局部均值滤波

非局部均值滤波算法是由Buades等人提出[21].该算法认为目标像素不仅和周围像素有关,也与整幅图像的像素有关,因而目标像素的值是基于整幅图像中的相似像素计算得到.由于单个像素之间的相似性不能准确判断,而图像块不仅能表示图像的灰度分布特性,还能表示图像的几何结构特性,因而该算法采用图像块的方式来寻找相似像素.

对于一幅图像,它的目标像素值是由整幅图像中所有与它相似的像素进行加权平均得到的.其权值是由以目标像素为中心的图像块与以其他像素为中心的图像块之间的高斯加权欧式距离来决定的.具体计算如下:

(7)

其中,v为含噪图像,u为降噪图像,i为目标像素点.ω(i,j)为权值,它的值由以像素点i,j为中心的图像块之间的欧式距离计算得到,它表示像素点i,j之间的相似度.计算公式如下:

(8)

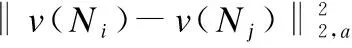
(9)

根据公式(7)～公式(9)可知,非局部均值滤波利用了图像的结构相似性信息,以图像块的方式进行滤波,用图像块之间的高斯加权欧式距离来决定像素之间的相似度程度和权值的大小,最后将目标像素与图像中所有和目标像素相似的像素进行加权平均得到降噪后的像素值.该算法能够尽可能多的保留图像的纹理细节,获得较好的降噪效果.

由于莱斯校正的非局部均值滤波算法不仅考虑了DWI图像的噪声为莱斯分布的特点,还考虑到了图像纹理细节的特点.因此该算法不仅能够较大程度地减少DWI图像中的噪声,同时也能够更有效地保留DWI图像中的纹理细节信息,提高数据的准确度,更好地实现了DWI图像的降噪.

4 实验结果

为了证明非局部均值算法应用于DWI降噪的有效性,本文实验分为两个部分进行:模拟数据实验和真实数据实验.

4.1 模拟数据

通过建立模拟张量场对DWI图像进行加噪,再分别用各向异性扩散算法(PM算法),全变分算法(TV算法),线性扩散算法,扩散系数自适应选择的各向异性扩散算法(ACS算法)[22],传统的非局部均值滤波算法(NLM算法)以及莱斯校正的非局部均值算法(RCNLM算法)对DWI图像进行降噪,观察降噪效果.实验使用扩散加权方向为六个扩散方向,其方向编码如表1所示.

表1 六个编码方向的梯度编码Table 1 Gradient coding for six coding directions

实验所用模拟数据是由7幅大小为128×128的DWI图像组成,包括一幅未加权图像S0及6幅根据表1所示的扩散加权方向进行加权所得到的DWI图像S1～S6.我们采用椭球模型来建立模拟张量场,但由于图像过大张量不便显示,于是选择了相同位置大小为15×15的张量视图.根据这7幅模拟数据计算得到的原始不含噪的张量场如图1(a)所示.对7幅DWI图像S0～S6加入σ=40的高斯噪声,根据含噪DWI计算得到的含噪张量场如图1(b)所示.然后,分别采用PM,TV,线性扩散,ACS,NLM以及RCNLM降噪算法对DWI图像进行降噪,并根据降噪后的DWI图像计算DTI,实验结果如图1所示.

对比图1(a)与图1(b)可以看出,由于噪声的存在对张量计算产生较大影响,使得到的原本排列整齐的张量场变得杂乱无章.图1(c)～图1(h)是分别用PM、TV、线性扩散、ACS、NLM以及RCNLM算法对DWI图像进行降噪处理后计算得到的张量图.

从图中可以看出,RCNLM算法处理后所得到的张量图,各张量排列整齐,张量大小形状一致,更加接近原图,降噪效果最好.通过对比各算法可知,ACS算法和NLM算法得到的张量其张量方向无太大变化,但形状仍有细微的偏差.PM算法得到的张量其张量方向具有较大偏差,而RCNLM算法得到的张量方向则基本与原图相同,偏差较小.TV算法与线性扩散算法能够得到理想的张量方向,但张量的形状大小具有明显偏差,而RCNLM算法则比较理想.

为了客观的说明上述算法的降噪效果,本文采用了峰值信噪比(Peak Signal to Noise Ratio,PSNR),结构相似性(Structural Similarity,SSIM)和均方误差(Mean Squared Error,MSE)作为评价标准.峰值信噪比表示的是最大可能信号和噪声之间的比值,该值越高,表明降噪图像所含的噪声越少且与原始图像差异越小;而结构相似性的值在0与1之间,它的值越接近1说明降噪图像与原始图像的结构细节相似度越高.不同的噪声水平在模拟张量图中使用各类算法降噪结果评价值如表2所示.

图1 原始张量场和含噪张量场以及各算法降噪结果Fig.1 Original tensor field,noisy tensor field and denoised tensor field calculated after the denoising by each algorithm

表2 各类降噪算法降噪后的评价值
Table 2 Evaluation values of denoised image by using various denoising algorithms

标准差评价指标PMTV线性扩散ACSNLMRCNLMσ=40PSNR75.970781.037678.332186.205594.930196.2857SSIM0.62100.81920.74030.74690.87500.9855MSE0.00170.00060.00100.00020.000020.00002σ=50PSNR76.037680.394779.441686.195491.135195.7541SSIM0.57820.73770.69330.72270.79810.9776MSE0.00170.00070.00080.00020.000070.00002σ=60PSNR75.941580.324778.800985.883391.782394.8195SSIM0.56610.70980.64690.66740.77580.9669MSE0.00170.00070.00090.00020.000060.00003

从表2中可以看出,在同一噪声水平下RCNLM算法的MSE值最小,PSNR值和SSIM值都最高.并且,随着噪声水平的增加,噪声对图像的影响加大,其他几种算法的PSNR值都在减小,而RCNLM算法的PSNR值仍然保持较高水平,说明该算法的抗噪性能优于其他算法.以上数据表明通过使用RCNLM算法对DWI图像进行降噪能够得到较好的效果,提高了张量计算的准确度.

4.2 真实数据

本文实验采用脑部核磁共振扩散张量图像,实验数据是从网站MathWorks[注]http://www.mathworks.com/matlabcentral/fileexchange/21130-dti-and-fiber-tracking中获得的.其中每幅图像的大小是128×128像素,扫描层为58层,每层有7幅图像其中包含一幅未加权的MRI图像和施加了6个不同方向的梯度脉冲获得的DWI图像.扩散敏感系数b=1000s/mm2.分别用各类降噪算法对DWI图像进行降噪,并对降噪后的图像进行神经纤维跟踪处理,通过跟踪结果来判断降噪效果.

实验对真实数据分别采用各降噪算法进行降噪,根据降噪图像计算得到DTI数据,然后采用经典的纤维连续跟踪法(Assignment by Continuous Tracking,FACT)算法[23]对DTI数据进行神经纤维跟踪.跟踪结果如图2所示.

图2(a)～图2(f)是分别用TV、PM、线性扩散、ACS、NLM以及RCNLM算法对DWI图像降噪后跟踪到的神经纤维图.从图中可以看出,RCNLM算法处理后得到的神经纤维图中纤维密度明显较大,纤维普遍较长且平滑.通过对比其他算法可知,使用PM算法和线性扩散算法进行降噪处理后跟踪得到的神经纤维中存在角度弯曲过大的纤维,这在人体大脑中是不可能存在的,而RCNLM算法跟踪到的神经纤维中则没有这种弯曲角度过大的纤维.其他的算法的纤维密度明显要稀疏.由图2的黑色方框中可以看到,RCNLM算法处理后得到的神经纤维中较好的跟踪到了该条神经纤维,而使用NLM算法处理后得到的神经纤维中并没有跟踪到该条神经纤维.在使用同一种神经纤维跟踪算法的情况下,以上各个降噪算法得到的跟踪结果各有不同,而RCNLM算法的效果最好,跟踪到的神经纤维不仅密度大且较为平滑.

对于真实数据,在对神经纤维跟踪效果好坏的判断方面,常用的方法是采用神经纤维数量和最长纤维长度来说明跟踪效果[10].但是由于噪声的影响,会使较长的纤维被错分为几根较短的纤维,从而出现被跟踪出来的纤维又短又多的情况.因此以纤维数量和最长纤维长度来判断降噪效果并不可靠,本文提出用平均纤维长度来判断降噪效果,平均纤维长度越长则跟踪到的纤维更均匀平滑,能较好的说明降噪效果.平均纤维长度的计算如下:

图2 使用各类降噪算法对DWI图像进行降噪后跟踪到的神经纤维图Fig.2 Nerve fiber maps obtained by tracking the denoised images that obtained by using various denoising algorithms

(10)

其中,n表示为纤维数量,length表示每条纤维长度.

用平均纤维长度来对各算法降噪处理后跟踪出来的神经纤维进行统计,其结果如表3所示.

表3 神经纤维跟踪数据Table 3 Nerve fiber tracking data

从表3的统计数据中可以看出,使用RCNLM算法进行降噪后得到的降噪图像,其跟踪得到的神经纤维平均长度最长,说明得到的神经纤维长度普遍较长,其有效性更高.而使用线性扩散算法进行降噪后跟踪得到的神经纤维数量最多且最长纤维长度最长,根据图2(d)中可以看到,该算法得到的神经纤维中有由于错误跟踪得到的神经纤维,因此进一步说明以纤维数量和最长纤维长度来判断其效果是不可靠的.综合以上数据可知,使用RCNLM算法对DWI图像进行降噪能够取得非常满意的降噪效果.

5 结束语

本文根据DWI图像结构相似性程度高以及图像中所含噪声为莱斯噪声的两个特点,提出将莱斯校正的非局部均值算法应用于DWI图像的降噪,先对含有莱斯噪声的图像进行莱斯校正,再对莱斯校正后的图像使用非局部均值滤波器对其进行降噪,最后得到降噪图像.非局部均值滤波器利用了图像本身纹理和结构具有重复出现的特性,通过使用图像块的方式对图像进行降噪,它能够较大程度的减少噪声同时也能尽可能多的保留DWI图像中的纹理细节信息.本文采用模拟实验与真实数据的实验对本文算法进行验证,并将本文算法与目前DWI降噪中常用的一些算法进行比较.实验结果表明,本文所提出的莱斯校正的非局部均值滤波算法取得的降噪效果较好,保留了DWI图像中较多的纹理细节信息,提高了DTI数据的准确度,使后续的处理结果更具有效性.