基于边权的稳定标签传播社区发现算法

张 蕾，钱 峰，赵 姝，陈 洁，张燕平，刘 峰

1(安徽大学 计算机科学与技术学院，合肥 230601) 2(铜陵学院 数学与计算机学院，安徽 铜陵 244061)

1 引 言

近年来，复杂网络在许多领域得到广泛应用，如社交网络、万维网、科学家合作网络、神经网络、蛋白质交互网络和语言学网络[1]等.众多研究表明，复杂网络具有社区(集群)的属性.在社区内部，成员间关系紧密，但不同社区的关系疏远.这一特性反映复杂网络极其普遍和重要的拓扑结构，即内聚倾向，对理解复杂网络的结构和功能非常重要.

为挖掘复杂网络中社区结构，研究者们已经提出大量的算法，包括模块度优化算法[2，3]、谱聚类算法[4，5]、层次挖掘算法[6，7]、标签传播算法(LPA)[8，9]等.其中，LPA是目前为止最快的社区挖掘算法之一.2007年，Raghavan等人[10]提出经典标签传播算法(Label Propagation Algorithm，LPA).该算法设计简单、无参数、近乎线性的复杂度和收敛周期短，特别适用于大型网络的社区发现，因此得到大量学者的关注.

然而，经典LPA存在一些缺陷，如高随机性、易形成巨型社区等.当相邻节点具有相同的标签时，节点会随机选择标签，使得算法输出结果具有较高随机性，极大地影响算法稳定性.另外，当大型社区的社区标签停止传播时，若邻近小社区的标签还没有传播开，大社区的标签则会影响小社区的标签，致使小社区被吞噬，最终可能形成一个巨型社区.使社区发现结果的质量变得非常差.

近年来，许多学者对经典LPA算法中的缺陷进行改进.大致可分为两种策略.一种是通过约束目标函数改变标签的更新过程，如LPAm[11]、LPAm+[12].通过目标函数的优化手段可提高算法聚类性能.然而，这些算法没有考虑节点的重要性和不同标签的影响.因此输出结果仍然是随机的.另一种是通过计算节点重要性获取标签的影响，进而改变标签的更新顺序和规则，如NIBLPA[13]、NILPA[15].利用不同标签的影响打破标签传播过程的随机规则，因此可提高算法精度和稳定性.然而，这些算法利用节点的度数衡量节点重要性.虽然节点的度数可体现节点重要性，但却无法体现节点间的关系.由于依然平等看待网络中的所有节点，算法在进行标签传播时，不可以按随机顺序对节点标签进行更新，必须首先按重要性对节点进行排序，否则将导致算法准确率和稳定性下降，这将增加算法时间复杂度，随着网络规模的增大，消耗的资源也越多.在网络中，节点与其邻居的关系程度是不同的，这种不平等关系可依据节点的局部信息获得.换句话说，节点不会平等地看待其邻居，地位上的不平等决定节点标签影响力的不同，使得节点在从邻居中选择标签时具有偏向性，若利用偏向的程度使随机的标签选择转为固定的选择，便可解决标签传播算法稳定性差问题，而且利用局部优化的更新策略无需考虑节点的更新顺序，可提升算法运行效率.

为在稳定性与运行速度间实现一定的平衡，本文提出一种基于边权的标签传播算法(Stable Label Propagation Algorithm based on Edge Weights，SLPA_EW)用于社区发现，SLPA_EW算法首先利用三角结构度量节点不同邻居对其影响的程度，将度量结果作为节点间的边权.基于边权提出一种新的标签更新策略，新的策略依据边权计算节点邻居标签的影响力并选择影响力最高的标签.在标签初始化过程中，将边权互为最大值的邻节点形成节点对并赋予相同标签避免这些节点在更新过程中可能出现的标签振荡问题.在更新过程中，在标签更新策略中增加标签权重避免出现巨型社区.实验说明该算法在提高稳定性的同时，保障算法执行速度.SLPA_EW算法的优势主要有3点：

1)利用待更新节点与邻居间边的权重指导标签更新过程，消除标签选择和更新的随机性，提高算法稳定性.

2)在标签传播前，将易引起标签振荡现象的相邻节点组成节点对并分配相同的标签，进一步提高算法的稳定性，同时减小初始标签数量.

3)引入标签权重以限制社区形成规模，防止出现巨型社区.

本文其余部分组织如下.第2节介绍基于LPA社区发现方法的相关工作.第3节给出本文方法的基本定义和原理.第4节详细介绍本文方法(SLPA_EW)的具体步骤和分析.第5节给出本文方法在真实网络数据集上的实验和结果分析.第6节总结全文.

2 相关工作

经典LPA的基本思想是为每个节点初始化一个唯一的标签，然后节点根据随机顺序扩展标签.在标签传播阶段，每个节点从邻居中选择最大数量的标签更新自身标签.如果存在多个这样的标签，则随机选择一个.重复该过程直至所有节点的标签趋于稳定.最终，拥有相同标签的节点被划分到一个社区中.算法每次迭代复杂度为O(m)，经过较少迭代次数后算法即可收敛[8].

经典LPA提出后，许多学者对存在的一些问题对算法进行改进.这些问题主要包括以下两个方面.第一方面是社区结构模糊时算法失效问题；另一方面是传播过程中节点标签更新和选择随机性问题.这些问题最终导致社区划分结果稳定性和准确率下降.

标签的传播特性使标签容易在关系紧密的结构中进行传播.由于未限制标签的传播距离，经典LPA在多次迭代后，关系紧密的大社区很容易将自身的标签传播给与其相连的小社区，形成巨型社区，甚至出现网络中所有节点的标签相同，导致算法失效.为抑制出现巨型社区，2009年，Barer等人[11]提出LPAm算法，将模块度与标签传播算法相结合.通过给定一个目标函数，使得标签在传播过程中受到约束，通过最大化目标函数寻找最优的社区划分.解决算法失效问题.但是算法容易陷入模块度局部最大值而影响输出结果的准确性.2010年，Liu等人[12]提出LPAm+算法，将LPAm与多步贪心聚类算法(Multi-Step Greedy agglomerative algorithm，MSG)结合，利用MSG同时合并多个相似社区，解决LPAm算法易陷入局部最大值问题，提高算法的聚类性能.

由于依赖标签的频率指导标签的更新，经典LPA在待更新节点的邻居节点的标签中出现多个最大值时，会从中随机选择一个标签进行传播，导致算法每次运行输出结果都不相同.为减小随机性，2014年，Xing等人[13]提出NIBLPA 算法，该算法采取k-shell分解技术计算标签的影响力.在迭代过程中，选择具有最大影响力的标签更新节点标签，以提高算法稳定性和准确率.2016年，Shang等人[14]提出一种基于循环搜索的核心节点集，并根据节点的相似性为节点分配标签的改进算法.算法通过计算每个节点的度数并找出相邻节点中的最大度数的节点与其形成核心节点集.在更新过程中，利用相似性将核心节点集的标签分配给它们的邻居，减少算法随机性.2017年，Ma等人[15]提出NILPA算法，算法首先依据节点的度数计算节点的重要性并对节点按其重要性降序排序.在此基础上利用随机游走理论构造节点相似度矩阵.利用节点重要性和相似性矩阵形成新的节点关系度量标准指导标签更新过程，提高算法输出结果稳定性.但节点相似性的计算依赖于矩阵相乘，随着网络规模不断增大算法消耗的资源也越来越多.2018年，Zhang等人[16]提出一个结合节点权重的密度函数，并将其作为实现节点标签传播的目标函数.算法首先根据节点度数找出网络中影响力较大的核心节点集.然后，根据节点相似性为网络中的节点分配权重.提高影响力较大节点标签在标签传播过程中的优先级，有效地提高算法准确性.

LPA稳定性差的原因主要是由于平等看待网络中的每个节点.事实上，不同邻居对节点的影响程度可能不同，这会决定该节点标签的影响力，因此需要找到一种节点关系度量方法以区分影响的不同.在已有的节点关系度量方法中：如局部度量、全局度量和基于随机游走的度量.全局度量适合揭示重要节点，但计算成本较高.基于随机游走的度量需要利用矩阵通过多次迭代运算评估节点间的关系.这些方法都不适合处理大型网络.本文采取局部度量方法，K-shell分解是典型的局部度量方法，该方法利用节点的度中心性计算节点的重要性，忽略了节点间的关系.本文利用三角结构度量节点与其邻居间的关系程度并将度量结果作为节点间的边权.

3 基于边权的标签更新规则

本节将介绍边权的计算方法和基于边权的标签更新策略.新的更新策略使标签的随机选择变成确定选择，以解决随机性问题，提高输出结果稳定性.

3.1 边权的定义

随机性是经典LPA中最为严重的缺陷.由于仅考虑待更新节点的邻居中相同标签的个数，在每轮迭代中，节点从邻居中选择数量最多的标签更新自身标签，当出现多个选择时，则随机选择其中一个.特别是在第一轮迭代中，节点周围的标签个数都是相等的，导致随机性必然发生.这种随机性严重破坏算法健壮性和输出结果稳定性.

本文利用三角结构度量节点与其邻居间的关系程度并将度量结果作为节点间的边权.三角结构是指三个节点两两相互连接，是复杂网络中一种非常重要的结构特征.若连接两个节点的边参与形成的三角结构数量越多，则两者的关系越紧密.下面给出本文边权的计算方法.

定义1.边权.给定相邻节点i与j，其连接边e(i，j)的权重计算如公式(1)所示：

(1)

其中，wo(i，j)表示边e(i，j)原始的边权，对于无权图，wo(i，j)=1.N(i)表示网络中节点i的邻居集合.Δ(i，j)表示网络中涉及边e(i，j)三角结构的数量.依据式(1)的计算结果可以区分节点与其邻居间关系的紧密程度.

3.2 基于边权的标签更新规则

新的标签更新策略将基于节点间的边权，节点在更新自身标签前，需累加具有相同标签邻居的边权，选择累加值最大的节点标签更新自身标签.

定义2.节点标签的更新策略.节点i在进行标签更新时，需要从邻居的标签集合中选择一个更新自身的标签.基于边权的节点标签更新策略的形式化描述如公式(2)所示：

(2)

其中，L(i)表示节点i的标签，s(Lj)表示每一个标签为Lj的邻接节点与待更新节点i间的边权累加值.累加结果越大说明该标签的影响力越高，拥有影响力大的标签的节点容易将自身标签传播给相邻的节点，且自身的标签不易被更新.通过这种更新策略，消除标签选择的随机性，极大地增强算法稳定性，并使算法能快速收敛.

4 基于边权的稳定标签传播算法SLPA_EW

本节将介绍算法SLPA_EW的细节，并分析算法复杂度.SLPA_EW算法可分为两个阶段：初始化阶段和标签传播阶段.

4.1 标签的初始化

首先，通过邻接表及公式(1)对网络中每个节点计算该节点与所有邻居间连接边的边权.接着，为每个节点分配一个唯一的初始标签(节点编号)，标签作为节点的唯一标识用于标记节点所属的社区划分.

依据公式(2)，在第一轮迭代时，由于所有节点的标签尚未更新.每个待更新节点的邻居拥有的标签都是唯一且不同的.此种情况下，待更新节点会从其邻居中选择最大边权的节点标签更新自身标签.但存在这样的概率，若两相邻节点彼此边权互为最大值，在第一轮标签更新中，双方都会选择对方的标签更新自身标签，引起标签的振荡.振荡现象导致算法迭代次数增加，而且这些无意义的迭代会影响算法效率.为保证算法收敛速度和输出结果质量，在标签开始传播前，找出这些节点形成节点对并为这些节点对分配相同标签.这些节点对往往属于同一社区，且易为社区核心.通过该策略不仅可以解决振荡问题，而且可减少初始标签数量.

4.2 标签的选择和传播

节点在进行标签选择时，首先需累加所有邻居中拥有相同标签节点的边权，选择累加值最高的标签更新自身标签.为限制标签的无限传播，避免形成巨型社区.本文给所有标签设定权重并引入标签更新策略中，标签权重会随着社区规模的增长而减小，计算如公式(3)所示：

(3)

其中，Lc表示社区C的标签，dc表示社区C中所有节点度的总和，m表示网络中边的总数.引入标签权重后新的标签更新策略的形式化如公式(4)所示：

L(i)=arg max∑j∈N(i)[s(Lj)*Wl(Lj)]

(4)

其中，N(i)表示网络中节点i的邻居集合.依据式(4)，随着社区规模的增长，拥有相同标签的节点不断增加，标签的权重变得越来越小.因此标签传播能力随着社区尺寸增加而减少，防止产生巨型社区.

4.3 算法描述

为更好地描述本文算法，这里给出SLPA_EW算法的伪代码，如算法1所示.

算法1.基于边权的标签传播算法

输入：网络G=(V，E)

输出：社区划分结果

1) for eachi∈Vdo

2) for eache(i，j)∈AdjList[i] do

3) 依据式(1)计算边e(i，j)的权重w(i，j)；

4) end for

5) end for

6) for eachi∈Vdo

7)L(i)=i；/*对集合V中所有节点的标签进行初始化*/

8) end for

9) for eachi∈Vdo

10) 在节点i的邻居中找到拥有最高权重的边，

将结果保存至列表T[i，j]；

11) end for

12) 建立图G′(V，E′)，循环从G中读取节点添到G′中，图G′的初始边集E′为空；

13) for eachi∈Tdo

14) for eachj∈Tdo

15) ifT[i][0]=T[j][1] andT[i][1]=T[j][0] then

16) 将边e(i，j)加入到图G′中；

17) end if

18) end for

19) end for

20) 搜索图G′中所有的连通分支；/*找出节点对*/

21) 对每个连通分支中节点的标签重新分配为该分支

中的最小节点编号；/*给节点对分配相同的标签*/

22) While图中所有的节点标签未稳定

23) for eachn∈Vdo

24)L′n=arg max∑i′∈Nn(Li′)w(i′,n)W(Li′)；

/*依据式(4)进行标签更新*/

25) end for

26) if (标签更新循环结束) then

27) 执行多步贪心聚类算法(MSG)；/*计算模块度，

合并使模块度增加的社区*/

28) end if

29) end while

代码1～8行，计算每个节点与其邻居间的边权并对所有节点标签进行初始化.代码9～21行，在标签开始传播前，首先找到互为权重最大值的邻接节点，通过构建连通分支的方法将其形成节点对，之后对这些节点对分配相同的标签避免传播中可能出现的标签振荡现象.为避免算法有陷入局部最大值的倾向，导致社区的划分结果不能真正反映网络的结构，影响输出结果的准确性.本文采取文多步贪心聚类算法[12](MSG)避免陷入局部最优.代码26～28行，在标签更新循环结束后，对输出结果做进一步处理，利用MSG合并使模块度增加的社区.由于篇幅关系，关于MSG的详情本文不在赘述.虽然此举增加算法复杂度，但可提高社区划分质量.

4.4 算法复杂度分析

算法的复杂度估计如下.假设网络中包括n个节点以及 m 条边.整个算法包含两个阶段，第一阶段是计算边权和标签初始化过程.计算边权复杂度为O(2m)；寻找节点最大边权复杂度为O(2m)；构造节点对复杂度为O(n2)；节点标签初始化复杂度为O(n).第二阶段是标签传播过程.每一次迭代O(n)；利用MSG进行社区合并复杂度为O(mlogn)[12]. 最后算法收敛遍历输出社区复杂度为O(n).

5 实验结果与分析

本节使用九种真实网络数据集评估本文算法的性能，采用模块度函数Q[17]评价社区划分质量，对比算法包括经典LPA[10]、LPAm+算法[12]和NILPA算法[15].实验环境为，处理器 Intel i3-4170 3.70 GHz，内存4G，Win 7操作系统.相关代码均基于Anaconda3环境采用Python语言开发.

5.1 实验数据和评价指标

实验选取9种真实网络数据集：7种取自Newman数据集[注]http：//www-personal.umich.edu/～mejn/netdata/，分别是空手道俱乐部网络(Karate)、海豚社交网络(Dolphins)、美国大学橄榄球网络(Football)、共同作者网络(Netscience)、电网网络(Power)、互联网快照网络(Internet)、凝聚态物质协作网络(Cond-Mat)；两种取自SNAP数据集[注]http：//snap.stanford.edu/data/，分别是文件共享网络(p2p-Gnutella)和安然电子邮件网络(Enron-Email).基本信息如表1所示.

因为多数真实网络数据集社区结构是未知的，所以本文采用模块度函数Q(Modularity)衡量社区划分结果质量.虽然函数Q存在一些缺陷，但它仍是目前最常用的一种社区质量评价指标.函数Q的定义如公式(5)所示：

(5)

其中：m表示边的总数；Aij表示邻接矩阵，如果节点i和节点j之间存在边，Aij= 1，否则Aij=0；di和dj分别代表节点i和节点j的度数；Ci和Cj分别表示节点i和节点j所属的社区，当i和j属于同一个社区时，δ(Ci，Cj)=1，否则δ(Ci，Cj)=0.

5.2 实验结果和分析

实验中，因为标签传播算法输出结果具有一定随机性，所以所有实验都运行100次.通过对实验结果波动范围进行分析，比较算法效率和稳定性.

表1 真实网络数据集Table 1 Real network datasets

1)运行效率分析

运行速度快和快速收敛是标签传播算法的最大优势.为验证SLPA_EW算法是否继承该优点，对四种算法分别在表1给定的不同规模网络上进行实验，然后计算这些算法运行100次后的运行时间和迭代次数的均值.实验结果如图1和图2所示.可以看到，经典LPA算法在不同规模的网络中运行时间最短，这归结于算法近乎线性的复杂度.改进后的算法虽然避免原始算法的一些缺陷，但导致算法时间复杂度的增加.其中LPAm+算法是基于模块度的，NILPA需要利用矩阵计算节点间的相似性，这些因素导致算法计算量增大.随着网络规模的增大，其运行时间也成倍的增长.相比而言，SLPA_EW算法在数据量增大的情况下依旧能够快速得出结果.实验结果表明本文算法拥有接近线性的时间复杂度，能够较好地处理大型复杂网络数据.

图1 真实网络数据集上的平均运行时间对比Fig.1 Comparison of average running time on real network datasets

在平均迭代次数对比结果中.SLPA_EW 算法在各个数据集上迭代次数都控制在10以下，这是因为SLPA_EW 算法避免很多不必要的更新.与其它三种算法相比，能有效控制算法迭代次数.

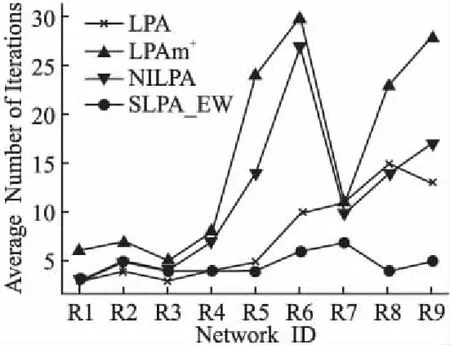
图2 真实网络数据集上的平均迭代次数对比Fig.2 Comparison of average iterations on real network datasets

2)模块度对比

为比较算法稳定性，将四种算法应用在九种真实网络数据集上进行社区发现，实验中，每个算法在每个网络分别运行100次，其中Qavg表示平均模块度，Qmin 和Qmax分别是对每一个真实网络做100次实验后求取的最差结果和最优结果.结果如表2所示，其中加粗的数据表示四种算法中对应每一个网络的最好结果.从表2中可以看出，SLPA_EW算法和NILPA算法在所有的数据集上依据最终输出结果求得的Q值均一致.说明算法输出结果的稳定性.

表2 模块度对比Table 2 Comparison of modularity

从实验结果看，LPAm+算法的模块度明显高于其他几种算法.尽管 SLPA_EW 算法没有在最高模块度方面取得最好的结果，但是算法在运行时间和迭代次数上仍是最有优势的.在多数网络上，算法的模块度接近最优模块度.总体而言，SLPA_EW 算法相比其它三种算法提高社区发现的准确率和稳定性.尤其在较大规模的网络算法，算法的优势更加明显.

6 总 结

针对经典LPA算法缺陷，通过改进标签初始化过程和更新策略，提出一种稳定的标签传播算法SLPA_EW用于社区发现.算法首先计算每个节点与邻居间的边权.在节点标签更新过程中，拥有相同标签的邻居节点与该节点之间的边权累加值决定节点是否将其更新为自身标签，这样的规则避免标签选择的随机性，使算法稳定性得以提高.在标签传播前，找出易引起标签振荡的节点对并对其赋予相同的标签，避免传播期间可能出现的振荡问题，同时减少初始标签数量.在每次迭代中，基于MSG，通过合并那些使模块度增加的社区以避免陷入局部最优解.算法收敛后，具有相同标签的节点被划分为一个社区.通过在真实网络数据集上的实验表明，所提算法能够保障输出结果的稳定性和较高的Q值，并且拥有较低的运行时间和迭代次数.在下一步工作中，将改进节点标签影响力的度量办法，进一步提高算法输出结果的质量.