拦截大气层内机动目标的自适应积分滑模制导律
2019-02-15黄景帅张洪波汤国建包为民
黄景帅,张洪波,汤国建,包为民, 2
(1. 国防科技大学空天科学学院,长沙 410073;2. 中国航天科技集团有限公司,北京 100048)
0 引 言
拦截末制导律的研究起始于20世纪30-40年代,早期的制导律以比例导引(Proportional navigation, PN)为主[1-2]。由于其结构简单、易于实现,因而成为工程应用最广泛的制导律。针对非机动或弱机动目标,PN能够取得优异的制导性能。但随着目标机动能力的提升,为了规避拦截系统通常会在拦截末段实施大幅度机动,PN由于未对目标机动进行专门处理导致其难以抑制由目标机动引起的弹目视线旋转,进而制导性能下降。由此,直接补偿目标加速度的增广PN应运而生,但其需要目标的加速度信息,通常难以精确获得[2]。为了有效拦截大机动目标,学者们基于先进控制理论设计了诸多制导律,期望产生优于PN的制导性能。
滑模变结构控制对模型不确定性和外部干扰具有较强的鲁棒性,因此广泛应用于末制导律的研究。Zhou等[3]采用基于趋近律的滑模控制设计了一种鲁棒的自适应滑模制导律,有效抑制了视线的旋转,终端脱靶量显著低于PN。文献[4]提出了一种含有广义的函数项的滑模变结构制导律,获得了对目标机动的鲁棒性,具有更小的过载峰值和拦截时间。由于末制导时间短,视线旋转角速率的收敛特性是影响制导性能的主要因素,但上述制导律仅保证了制导系统的稳定性,并没有涉及其收敛特性。基于有限时间稳定理论,文献[5-7]实现了视线旋转角速率在有限时间范围内收敛至零或其邻域。在上述鲁棒制导律的设计过程中,为了获得绝对的鲁棒性,需要引入以目标机动的上界为增益的切换项来消除未知的目标机动干扰[3-7]。但是,切换项中的符号函数是非连续的,易引起制导指令的抖振,降低抖振最简单的方法是用连续函数近似替代符号函数,例如饱和型函数、Sigmoid型函数[3-8]。除抖振外,目标机动的上界通常也难以确定,偏大会恶化抖振,偏小会缺乏鲁棒性。
为了较好地对付目标机动,控制视线转率有限时间收敛,同时降低抖振,文献[9]利用非线性干扰观测器对目标加速度进行估计,并补偿到有限时间收敛制导律中,精确拦截机动目标的同时又有效降低了抖振。与文献[9]类似,文献[10]设计了一种有限时间收敛的制导律,并联合扩张状态观测器对目标加速度进行估计。虽然实际仿真中上述观测器的收敛速度较快,但由于无法避免估计误差,且误差受系统初始状态的影响,因此难以定量给出误差的上界,进而系统的稳定性和视线转率的有限时间收敛性难以严格证明。文献[11]基于有限时间干扰观测器和新型的自适应趋近律设计了一种有限时间制导律,不需要观测误差的上界。与利用观测器补偿目标机动不同,在鲁棒的滑模控制的基础上,文献[12-14]将加速度视作上界未知的外界干扰,采用自适应估计算法对其上界进行逼近,并证明了饱和函数替代符号函数后制导系统的渐进稳定性,消除了抖振。文献[15]利用自适应控制方法估计干扰上界平方的同时,设计了一种固有光滑的有限时间制导律,证明了制导系统的各状态在有限时间内收敛至零的邻域。抑制制导指令的抖振与控制视线转率的有限时间收敛是鲁棒制导律的两个重要的制导品质,从以上分析可知,抖振问题已能够得到很好地解决甚至消除。但是,视线转率有限收敛的时间尚难以灵活精确地控制,收敛时间过长会超出末制导的飞行时间,快速地收敛通常意味着更多的控制消耗,而且有时是不必要的。
鉴于机动目标多数在大气层内飞行或实施机动,例如高超声速飞行器、机动弹头和战斗机等,于是本文针对大气层内机动目标的拦截问题,在上述研究成果的基础上,为了更灵活精确地控制视线转率有限收敛的时间,同时兼顾控制消耗,设计了视线转率收敛速率可调整的标准剖面,采用积分滑模控制方法跟踪标准剖面,同时结合自适应控制方法估计目标机动干扰上界的平方,最终推导得到了自适应的积分滑模制导律,并证明了积分滑模变量、跟踪误差与其积分均可在有限时间内收敛至零的邻域。为了适用于大气层内拦截,对所设计的制导律进行了微分几何形式的转换,使其作用方向垂直于导弹速度。通过仿真,验证了制导律的有效性。
1 导弹-目标空间拦截模型
为了研究导弹与目标间的相对运动,将两者均看作质点,则导弹末段拦截目标的空间交战场景可由图1表示。图中,oIxIyIzI为惯性坐标系,M和T分别代表导弹和目标,由M指向T的矢量r为弹目视线(Line of sight, LOS)方向,vm和vt分别表示导弹和目标的速度。

图1 弹目拦截交战Fig.1 Intercept engagement between missile and target
由图1可知,弹目相对运动的位置关系为
r=rt-rm=rer
(1)
式中:r为弹目之间的相对距离,er为视线方向上的单位矢量。因为目标相对于导弹的位置变化,视线在惯性空间中会产生旋转,设其旋转角速度为ω。由于视线的旋转完全决定于导弹和目标的速度在垂直视线方向上的分量,因此视线的旋转角速度垂直于视线,且
(2)
式中:v=vt-vm,eω为ω方向上的单位矢量,ω为视线旋转的角速度大小,简称视线转率。求取式(1)的时间导数并联立式(2)得
(3)
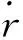
为了定量描述弹目的相对运动,本文采用文献[16]提出的视线旋转坐标系。相比于文献[6,9]所示的视线坐标系,由此建立的方程形式简洁,不存在耦合。定义单位矢量eθ=eω×er,(er,eθ,eω)构成的直角坐标系即为视线旋转坐标系,原点位于导弹的质心处,er和eθ张成的平面称为交会平面,eω为该平面的法向。基于上述定义,可得如下关系[16]:
(4)
式中:Ω为交会平面旋转角速度大小。对式(3)继续求导并联立式(4)可得弹目相对运动的标量方程组为

(5)
式中:atr、atθ与atω为目标加速度在视线旋转坐标系下的三个分量,amr、amθ与amω为导弹加速度在视线旋转坐标系下的三个分量。式(5)表明,交会平面内的相对运动与其转动是解耦的。
在进行制导律设计之前,作如下假设。
假设1. 忽略导弹导引头和控制系统的动态特性,认为其可以实现理想的制导过程。
假设2. 目标的机动幅值是有限的。

2 自适应积分滑模制导律
2.1 制导律设计
拦截制导律设计的基本原则是抑制视线的旋转,将导弹控制在与目标组成碰撞或准碰撞三角形的位置上[4]。由式(5)可知,通过设计合理的amθ即可控制ω的变化。
令vθ=rω,则式(5)的第二式可表示为
(6)
定义如下误差变量
e=vθ-vθc
(7)
式中:vθc为vθ的期望值。vθc的剖面表达式设计为
(8)
式中:r0和ω0分别为拦截初始时刻r和ω的相应值,Δ≥0,η≥1。由式(8)可知,当r→0时,vθc→Δ,通过改变η可调整vθc的收敛速率,且初始时刻的e值取为零,为了防止拦截起始阶段的导弹过载过大。

(9)
式中:atθ和amθ分别为系统的干扰和控制输入。本文的目标是设计合适的amθ,在未知有界干扰atθ存在的条件下,使系统状态有限时间内收敛至零或其邻域内。取如下形式的积分滑模面[17]:

(10)
式中:t≥t0,l1>0,l2>0, 0<α<1, sgn(·)为符号函数。滑模变量s(t0)=0意味着在拦截起始时刻系统状态即位于滑模面上。对式(10)求导并联立式(9),可得
(11)
设定如下的快速趋近律:
(12)
式中:k1>0,k2>0, 0<μ<1。联立式(11)-(12),可得积分滑模制导律(Integral sliding-mode guidance law, ISMGL)的表达式为
(13)
式(13)包含未知的目标加速度项atθ,致使其无法应用,为此采用自适应控制方法对|atθ|上界的平方进行估计。根据假设2,可设|atθ|≤d,d为正常数,引入如下形式的自适应律对κ=d2进行估计[15]:
(14)

(15)

(16)
式中:satδ1(x1)为饱和函数,表达式为
(17)
satδ2(x2)与satδs(s)以此类推。
2.2 稳定性分析
在对AISMGL进行稳定性分析之前,先给出需用的引理。
引理1[18]. 定义在包含原点的邻域U⊂Rn上的光滑正定函数V(x,t),若存在实数a、b>0, 0<γ<1,使得下式成立:
(18)
则该函数值将在有限时间内收敛至零,且收敛时间满足
(19)
式中:x(t0)=x0,t0为初始时刻。
引理2[19]. 对于双重积分系统:
(20)
若采用如下形式的反馈律:
(21)
式中:g1>0,g2>0, 0<ϑ<1,则系统在原点处是有限时间稳定的。
定理1. 针对式(9)所示的非线性制导系统,若采用设计的AISMGL进行制导,有如下结论成立:
1) 滑模变量有限时间收敛至|s|≤Θ。
2) 系统状态分别有限收敛至|x1|≤Θ2和|x2|≤Θ3。
各收敛域的具体表达式为

(22)
式中:Θ1为与d、ζ和Θ有关的正常数,ζ定义见证明过程。
证. 取如下形式的Lyapunov函数:
(23)

(24)
(25)
联立式(25)和(14),代入式(24)可得
(26)
由基本不等式可得
(27)
将式(27)代入式(26)有
-χV1+ψ
(28)


(29)
对其求导得
(30)

(31)
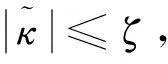
(32)
将式(32)改写成如下两种形式[20]:
(33)

(34)
同理,可得x2的收敛域为
(35)
证毕。
3 制导指令转换
根据制导指令作用方向的不同,拦截制导律可主要划分为垂直导弹速度和弹目视线两类。由于大气层内拦截弹利用气动力提供机动过载,大气层外的拦截弹利用安装在弹体质心处的轨控发动机提供机动过载,因此垂直导弹速度和弹目视线的制导律分别适用于大气层内和外的拦截。鉴于式(16)表示的AISMGL的作用方向垂直于视线,为了应对大气层内的机动目标,采用如下形式的制导指令转换[21]:
(36)
式中:am为导弹的制导加速度,nm为垂直于导弹速度的单位矢量。
为了保证式(36)中的分母不为零,令
nm·eθ=λ
(37)
式中:0<λ≤1。同时,nm还须满足以下两约束[22]:

(38)
式中:tm为导弹速度方向上的单位矢量。联立式(37)-(38)可解得nm存在的条件为
1-(tm·eθ)2≥λ2
(39)
由式(39),将λ设置为
(40)
式中:σ>0足够小。由此,可获得两个满足条件的解,记作nm1与nm2。考虑到制导指令的连续性,应取满足如下条件的解:
(41)

4 仿真校验
为了校验AISMGL的有效性,对不同类型的机动目标实施了拦截仿真。同时,考虑现有的两种制导律与AISMGL作比较,分别为经典的PPN制导律和文献[10]中基于有限时间稳定理论与扩张状态观测器设计的微分几何制导律,简记为DGGL-FE。PPN的表达式为
am=N1ω×vm
(42)
式中:N1为有效导航比。DGGL-FE的表达式为
(43)
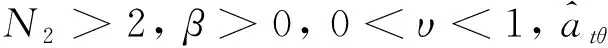
导弹和目标在惯性坐标系oIxIyIzI下的初始状态如表1所示。

表1 导弹和目标初始状态Table 1 Initial states of missile and target


(44)

基于上述拦截条件,仿真结果如图2-6和表3

表2 制导律参数Table 2 Parameter settings for guidance laws
所示。由图3可知,制导系统的状态变量快速地收敛至零附近,vθ较好地跟踪了设计的期望值vθc,表明了自适应算法抑制目标机动干扰的有效性。由于PPN未对目标机动做专门处理,在图4中相比于AISMGL与DGGL-FE,其视线转率无法得到有效抑制。DGGL-FE的视线转率在有限时间内收敛至零附近;由于η=2,AISMGL的视线转率呈准线性减小的趋势,与式(8)相吻合。图5给出了过载分布曲线,AISMGL的过载分布均匀。由于系统状态在拦截初始时刻即位于滑模面上,因此AISMGL的起始段过载较小,而DGGL-FE由于嵌入的观测器存在估计误差的初始尖峰现象,致使初始过载较大。在能量消耗方面,AISMGL明显优于PPN,且低于补偿目标加速度的DGGL-FE,表明控制视线转率提前收敛会消耗更多能量。

图2 拦截轨迹(情景一)Fig.2 Intercept trajectories (scenario 1)

图3 系统变量随时间变化(情景一)Fig.3 System variables versus time (scenario 1)

图4 视线转率随时间变化(情景一)Fig.4 LOSR rate versus time (scenario 1)

图5 制导加速度大小随时间变化(情景一)Fig.5 Guidance acceleration magnitude versus time (scenario 1)

制导律脱靶量/m总能量消耗/(m·s-1)AISMGL0.085411.16DGGL-FE0.203425.87PPN0.266582.44
情景二:目标正弦机动,参数设置与情景一相同,仿真结果如图7-11和表4所示。由仿真结果可知,与情景一相同,AISMGL的初始过载小,过载分布均匀。在脱靶量和总能量消耗方面AISMGL依然优于PPN,稍逊于DGGL-FE,表明此时控制视线转率尽早收敛可降低制导指令随着目标的正弦机动进行振荡的幅度,更有利于节省能量。

图7 拦截轨迹(情景二)Fig.7 Intercept trajectories (scenario 2)
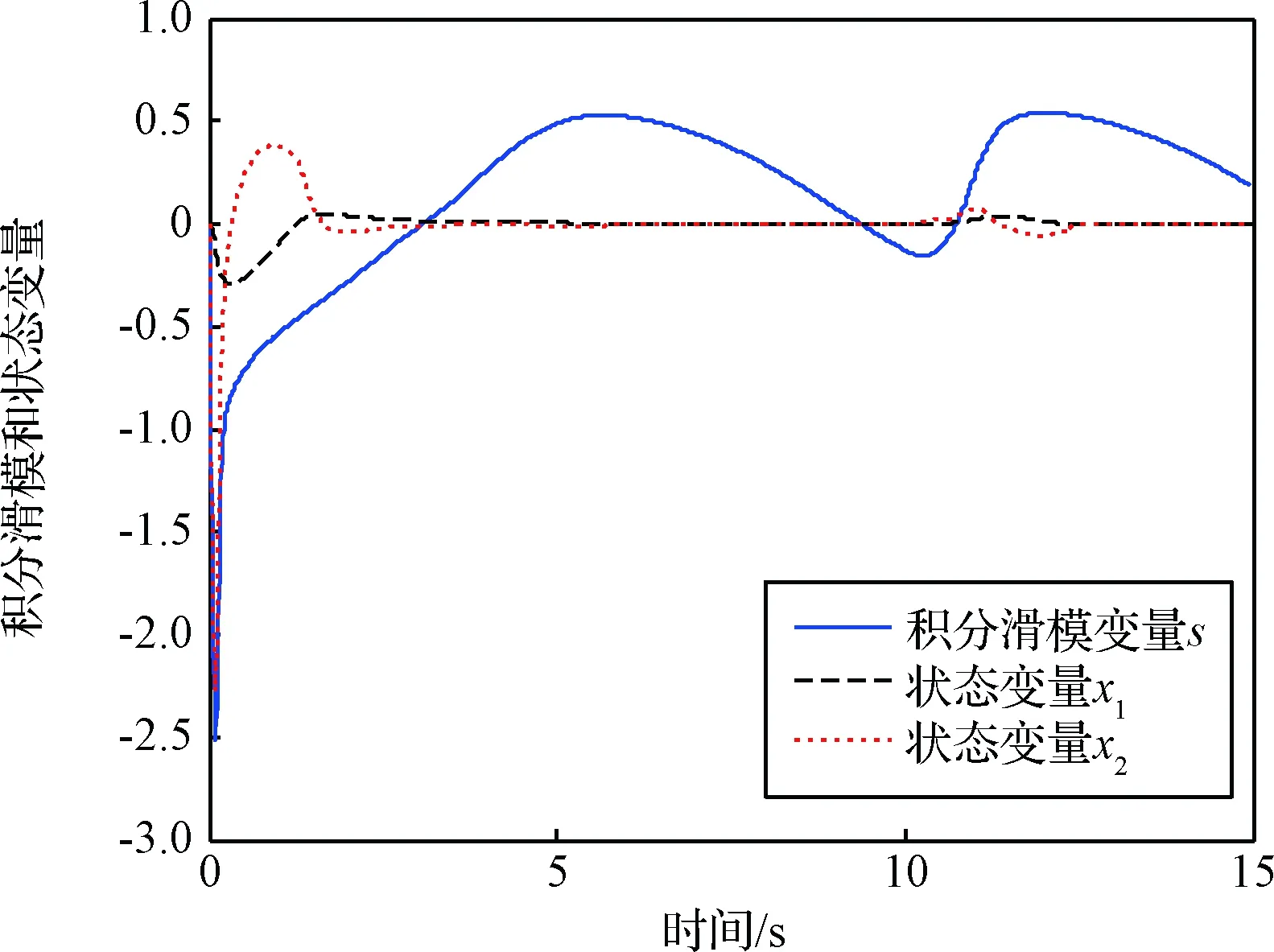
图8 系统变量随时间变化(情景二)Fig.8 System variables versus time (scenario 2)

图9 视线转率随时间变化(情景二)Fig.9 LOS rate versus time (scenario 2)

图11 能量消耗随时间变化(情景二)Fig.11 Energy consumption versus time (scenario 2)

制导律脱靶量/m总能量消耗/(m·s-1)AISMGL0.534461.91DGGL-FE0.480454.86PPN1.089478.88
与DGGL-FE相比,AISMGL可通过直接调节参数η来定量地控制视线转率的收敛速率,而DGGL-FE由于嵌入的观测器存在估计误差无法精确地给出视线转率的收敛时间。图12给出了不同η条件下拦截常值和正弦机动目标时视线转率的变化,η值越大其收敛速率越快。图13给出了脱靶量和总能量消耗随η的变化,脱靶量稍有波动,基本处于同一水平,不同机动形式下总能量消耗随η的变化趋势不同。
情景三:情景一与情景二均是在确定性的条件下实施的拦截仿真,但在实际的拦截中,制导信息不可避免地含有测量噪声。因此,为了验证所设计制导律的噪声特性,考虑相对距离、相对距离变化率、视线角和视线角速率的实际测量量中分别含有三倍标准差为10 m、10 m/s、0.01°和0.01/((°)/s)的高斯白噪声,并在上述仿真条件的基础上进行了300次的蒙特卡洛仿真,图14~图15分别给出了拦截常值和正弦机动目标时脱靶量和总能量消耗的统计结果。可看出,所设计的AISMGL具有良好的噪声特性,脱靶量和总能量消耗的波动范围较小,依然保持了确定性条件下的制导品质,易于工程实现。

图12 不同η下视线转率收敛Fig.12 LOSR convergences under different values of η

图13 脱靶量和总能量消耗随η的变化Fig.13 Miss distance and total energy consumption versus η

图14 常值机动的统计分布Fig.14 Statistical distributions of constant maneuvering
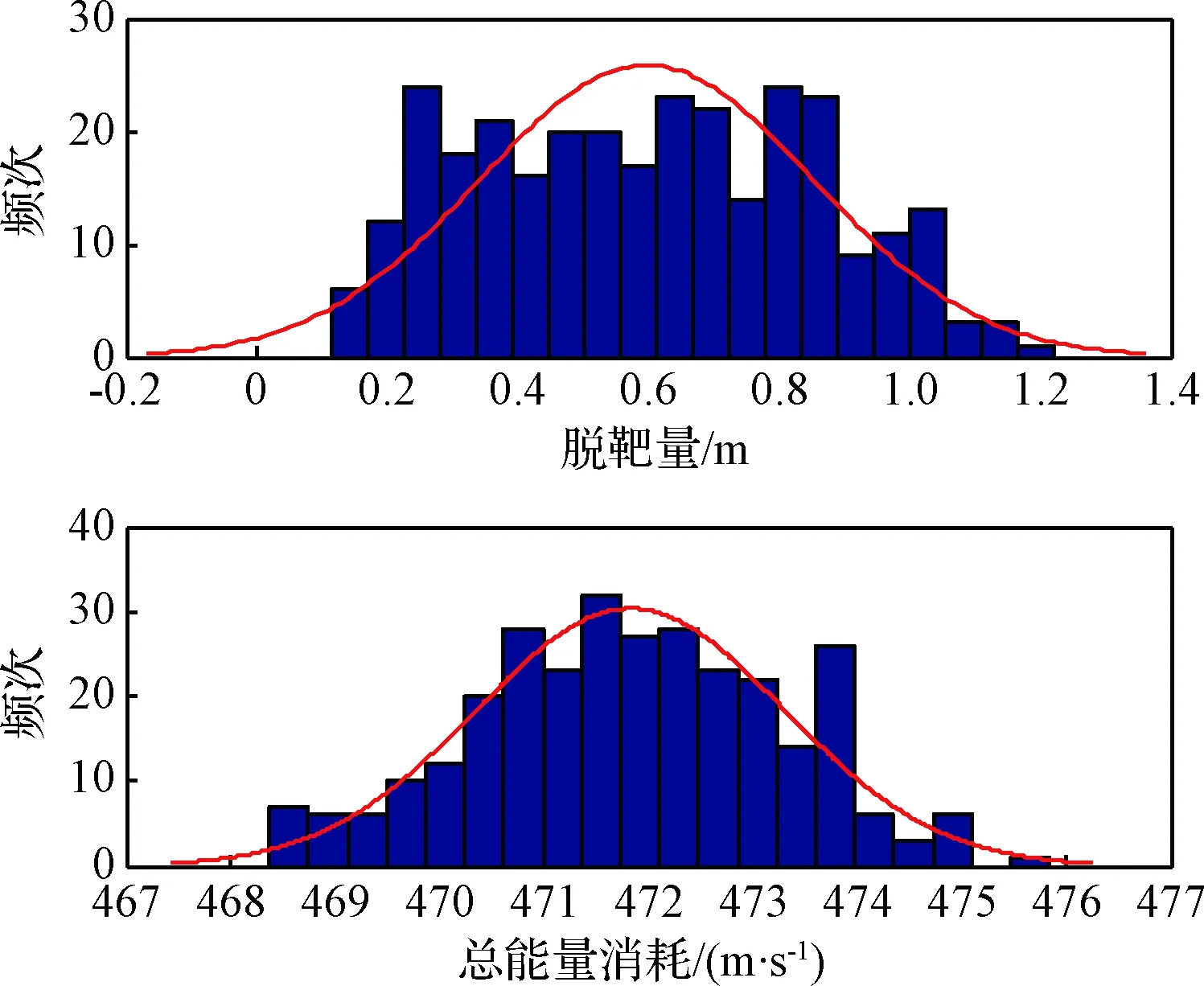
图15 正弦机动的统计分布Fig.15 Statistical distributions of sinusoidal maneuvering
5 结 论
本文从抑制弹目视线旋转的基本原则出发,设计了视线转率收敛速率可调的跟踪剖面,采用自适应积分滑模控制和制导指令转换方法推导了适用于拦截大气层内机动目标的自适应积分滑模制导律。仿真结果表明,文中所提出的制导律可精确命中机动目标,剖面跟踪误差能够在有限时间内快速收敛,并具有良好的噪声特性,易于工程实现。与已有制导律相比,可通过调整剖面参数灵活控制视线转率的收敛速率,过载分布均匀,能量消耗少。后续研究考虑如何智能地调整视线转率的收敛速率来进一步降低能量消耗。
